“Constrained texture mapping for polygonal meshes” by Levy

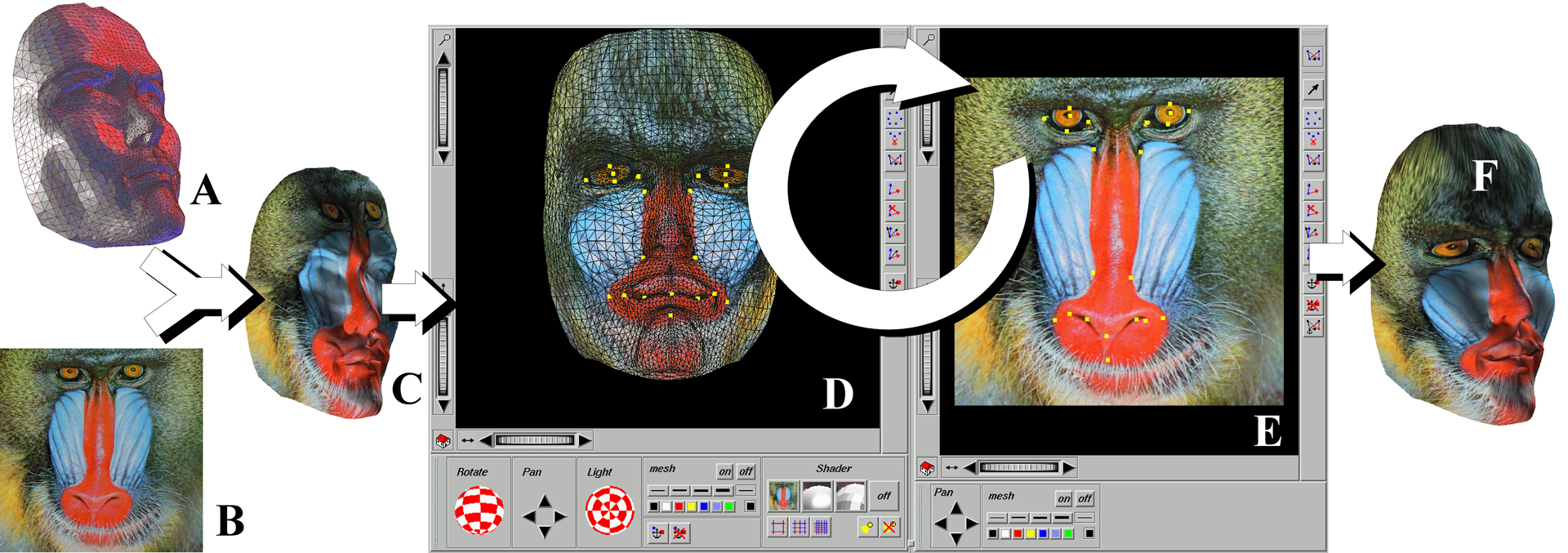
Recently, time and effort have been devoted to automatic texture mapping. It is possible to study the parameterization function and to describe the texture mapping process in terms of a functional optimization problem. Several methods of this type have been proposed to minimize deformations. However, these existing methods suffer from several limitations. For instance, it is difficult to put details of the texture in correspondence with features of the model, since most of the existing methods can only constrain iso-parametric curves.
We introduce in this paper a new optimization-based method for parameterizing polygonal meshes with minimum deformations, while enabling the user to interactively define and edit a set of constraints. Each user-defined constraint consists of a relation linking a 3D point picked on the surface and a 2D point of the texture. Moreover, the non-deformation criterion introduced here can act as an extrapolator, thus making it unnecessary to constrain the border of the surface, in contrast with classic methods. To minimize the criterion, a conjugate gradient algorithm is combined with a compressed representation of sparse matrices, making it possible to achieve a fast convergence.

1. Ashby, Manteuffel, and Saylor. A taxonomy for conjugate gradient methods. J. Numer. Anal., 27:1542-1568, 1990.
2. C. Bennis, J.M. Vezien, and G. Iglesias. Piecewise surface flattening for nondistorted texture mapping. In SIGGRAPH Comp. Graph. Proc., volume 25, pages 237-246. ACM, July 1991.
3. E. Bier and K. Sloan. Two-part texture mapping. IEEE Computer Graphics and Applications, pages 40-53, September 1986.
4. E. Catmull. A subdivision algorithm for computer display of curved surfaces. PhD thesis, Dept. of Computer Sciences, University of Utah, December 1974.
5. M. Eck, T. DeRose, T. Duchamp, H. Hoppe, M. Lounsbery, and W. Stuetzle. Multiresolution Analysis of Arbitrary Meshes. In Computer Graphics (SIG- GRAPH Conf. Proc.), pages 173-182. ACM, August 1995.
6. J. Eells and J.H. Sampson. Harmonic mapping of riemannian manifolds. Amer. J. Math., 86:109-160, 1964.
7. M.S. Floater. Parametrization and smooth approximation of surface triangulations. Computer Aided Geometric Design, 14(3):231-250, April 1997.
8. P.E. Gill, W. Murray, and M.H. Wright. Practical Optimization. Academic Press, 1981. ISBN 0-12-283950-1.
9. J.P. Gratier, B. Guillier, and A. Delorme. Restoration and balance of a folded and faulted surface by best-fitting of finite elements: principles and applications. Journal of Structural Geology, 13(1):111-1115, 1991.
10. Brian Guenter, Cindy Grimm, Daniel Wood, Henrique Malvar, and Frederic Pighin. Making faces. In Michael Cohen, editor, Proceedings of SIGGRAPH 98, Annual Conference Series, Addison Wesley, pages 55-66. Addison Wesley, 1998.
11. S. Haker, S. Angenent, A. Tannenbaum, R. Kikinis, G. Sapiro, and M. Halle. Conformal surface parameterization for texture mapping. IEEE Transactions on Visualization and Computer Graphics, 6(2), April-June 2000.
12. K. Hormann and G. Greiner. Mips: An efficient global parameterization method. In Curve and surface design: saint-malo 1999, pages 153-162. Vanderbilt university press, 2000.
13. K. Hormann, G. Greiner, and S. Campagna. Hierarchical parameterisation of triangulated surfaces. In Vision, Modeling and Visualization ’99, pages 219-226. infix, 1999.
14. V. Krishnamurthy and M. Levoy. Fitting Smooth Surfaces to Dense Polygon Meshes. In Computer Graphics (SIGGRAPH Conf. Proc.). ACM, August 1996.
15. A. W. F. Lee, W. Sweldens, P. Schroder, L. Cowsar, and D. Dobkin. Maps: Multiresolution adaptive parameterization of surfaces. Computer Graphics (Siggraph Conf. Proc), pages 95-104, July 1998. ISBN 0-89791-999-8. Held in Orlando, Florida.
16. B. Levy and J.L. Mallet. Non-Distorted Texture Mapping for Sheared Triangulated Meshes. In Computer Graphics (SIGGRAPH Conf. Proc.). ACM, July 1998.
17. S.D. Ma and H. Lin. Optimal texture mapping. In EUROGRAPHICS88, pages 421-428, September 1988.
18. J. Maillot, H. Yahia, and A. Verroust. Interactive texture mapping. In SIGGRAPH Comp. Graph. Proc., volume 27. ACM, 1993.
19. J.L. Mallet. Discrete smooth interpolation in geometric modeling. ACM- Transactions on Graphics, 8(2):121-144, 1989.
20. J.L. Mallet. Geomodeling. Academic Press, to appear, 2001.
21. Fabrice Neyret and Marie-Paule Cani. Pattern-based texturing revisited. In SIG- GRAPH 99 Conference Proceedings. ACM SIGGRAPH, Addison Wesley, August 1999.
22. Peachey and R. Darwyn. Solid texturing of complex surfaces. In SIGGRAPH Comp. Graph. Proc., volume 19, pages 287-296. ACM, July 1985.
23. H.K. Pedersen. Decorating implicit surfaces. In SIGGRAPH Comp. Graph. Proc., pages 291-300. ACM, 1995.
24. Samek, Marcel, C. Slean, and H. Weghorst. Texture mapping and distortions in digital graphics. The Visual Computer, 2(5):313-320, September 1986.
25. W.T. Tutte. Convex representation of graphs. In Proc. London Math. Soc., volume 10, 1960.