“Codimensional incremental potential contact” by Li, Kaufman and Jiang

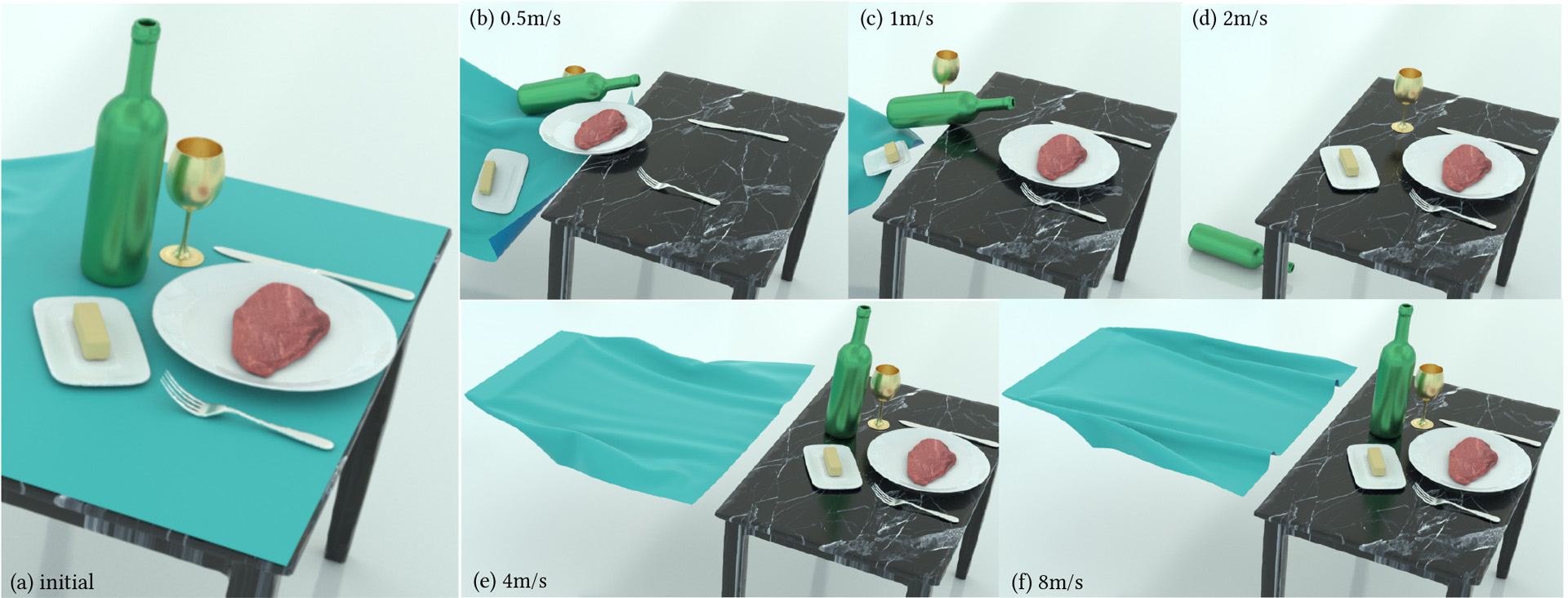
We extend the incremental potential contact (IPC) model [Li et al. 2020a] for contacting elastodynamics to resolve systems composed of codimensional degrees-of-freedoms in arbitrary combination. This enables a unified, interpenetration-free, robust, and stable simulation framework that couples codimension-0,1,2, and 3 geometries seamlessly with frictional contact. Extending the IPC model to thin structures poses new challenges in computing strain, modeling thickness and determining collisions. To address these challenges we propose three corresponding contributions. First, we introduce a C2 constitutive barrier model that directly enforces strain limiting as an energy potential while preserving rest state. This provides energetically-consistent strain limiting models (both isotropic and anisotropic) for cloth that enable strict satisfaction of strain-limit inequalities with direct coupling to both elastodynamics and contact via minimization of the incremental potential. Second, to capture the geometric thickness of codimensional domains we extend the IPC model to directly enforce distance offsets. Our treatment imposes a strict guarantee that mid-surfaces (respectively mid-lines) of shells (respectively rods) will not move closer than applied thickness values, even as these thicknesses become characteristically small. This enables us to account for thickness in the contact behavior of codimensional structures and so robustly capture challenging contacting geometries; a number of which, to our knowledge, have not been simulated before. Third, codimensional models, especially with modeled thickness, mandate strict accuracy requirements that pose a severe challenge to all existing continuous collision detection (CCD) methods. To address these limitations we develop a new, efficient, simple-to-implement additive CCD (ACCD) method that applies conservative advancement [Mirtich 1996; Zhang et al. 2006] to iteratively refine a lower bound for deforming primitives, converging to time of impact. In combination these contributions enable codimensional IPC (C-IPC). We perform extensive benchmark experiments to validate the efficacy of our method in capturing intricate behaviors of thin-structure contact and resulting bulk effects. In our experiments C-IPC obtains feasible, convergent, and so artifact-free solutions for all time steps, across all tested examples – producing robust simulations. We test C-IPC across extreme deformations, large time steps, and exceedingly close contact over all possible pairings of codimensional domains. Finally, with our strain-limit model, we confirm C-IPC guarantees non-intersection and strain-limit satisfaction for all reasonable (and well below – verified down to 0.1%) strain limits throughout all time steps.

1. David Baraff and Andrew Witkin. 1998. Large steps in cloth simulation. In Proceedings of the 25th annual conference on Computer graphics and interactive techniques. 43–54.Google ScholarDigital Library
2. Jan Bender, Dan Koschier, Patrick Charrier, and Daniel Weber. 2014. Position-based simulation of continuous materials. Computers & Graphics 44 (2014), 1–10.Google ScholarDigital Library
3. Jan Bender, Matthias Müller, and Miles Macklin. 2015. Position-Based Simulation Methods in Computer Graphics.. In Eurographics (tutorials). 8.Google Scholar
4. Jan Bender, Daniel Weber, and Raphael Diziol. 2013. Fast and stable cloth simulation based on multi-resolution shape matching. Computers & Graphics 37, 8 (2013), 945–954.Google ScholarDigital Library
5. Miklós Bergou, Basile Audoly, Etienne Vouga, Max Wardetzky, and Eitan Grinspun. 2010. Discrete viscous threads. ACM Trans. Graph. (TOG) 29, 4 (2010), 1–10.Google ScholarDigital Library
6. Miklós Bergou, Max Wardetzky, Stephen Robinson, Basile Audoly, and Eitan Grinspun. 2008. Discrete elastic rods. In ACM SIGGRAPH 2008 papers. 1–12.Google ScholarDigital Library
7. Kiran S Bhat, Christopher D Twigg, Jessica K Hodgins, Pradeep Khosla, Zoran Popovic, and Steven M Seitz. 2003. Estimating cloth simulation parameters from video. (2003).Google Scholar
8. Sofien Bouaziz, Sebastian Martin, Tiantian Liu, Ladislav Kavan, and Mark Pauly. 2014. Projective Dynamics: Fusing Constraint Projections for Fast Simulation. ACM Trans. Graph. (TOG) 33, 4 (2014).Google ScholarDigital Library
9. Robert Bridson, Ronald Fedkiw, and John Anderson. 2002. Robust treatment of collisions, contact and friction for cloth animation. In Proceedings of the 29th annual conference on Computer graphics and interactive techniques. 594–603.Google ScholarDigital Library
10. Tyson Brochu, Essex Edwards, and Robert Bridson. 2012. Efficient geometrically exact continuous collision detection. ACM Trans. Graph. (TOG) 31, 4 (2012), 1–7.Google ScholarDigital Library
11. George E Brown, Matthew Overby, Zahra Forootaninia, and Rahul Narain. 2018. Accurate dissipative forces in optimization integrators. ACM Trans. Graph. (TOG) 37, 6 (2018), 1–14.Google ScholarDigital Library
12. Rui PR Cardoso, Jeong Whan Yoon, Made Mahardika, S Choudhry, RJ Alves de Sousa, and RA Fontes Valente. 2008. Enhanced assumed strain (EAS) and assumed natural strain (ANS) methods for one-point quadrature solid-shell elements. Int. J. Numer. Methods Eng. 75, 2 (2008), 156–187.Google ScholarCross Ref
13. Juan J Casafranca, Gabriel Cirio, Alejandro Rodríguez, Eder Miguel, and Miguel A Otaduy. 2020. Mixing Yarns and Triangles in Cloth Simulation. In Computer Graphics Forum, Vol. 39. Wiley Online Library, 101–110.Google Scholar
14. Jumyung Chang, Fang Da, Eitan Grinspun, and Christopher Batty. 2019. A Unified Simplicial Model for Mixed-Dimensional and Non-Manifold Deformable Elastic Objects. Proceedings of the ACM on Computer Graphics and Interactive Techniques 2, 2 (2019), 1–18.Google ScholarDigital Library
15. Hsiao-yu Chen, Paul Kry, and Etienne Vouga. 2019. Locking-free Simulation of Isometric Thin Plates. arXiv preprint arXiv:1911.05204 (2019).Google Scholar
16. Hsiao-Yu Chen, Arnav Sastry, Wim M van Rees, and Etienne Vouga. 2018. Physical simulation of environmentally induced thin shell deformation. ACM Trans. Graph. (TOG) 37, 4 (2018), 1–13.Google ScholarDigital Library
17. Ming Chen and Kai Tang. 2010. A fully geometric approach for developable cloth deformation simulation. The visual computer 26, 6-8 (2010), 853–863.Google Scholar
18. Yanqing Chen, Timothy A Davis, William W Hager, and Sivasankaran Rajamanickam. 2008. Algorithm 887: CHOLMOD, supernodal sparse Cholesky factorization and update/downdate. ACM Transactions on Mathematical Software (TOMS) 35, 3 (2008), 1–14.Google ScholarDigital Library
19. Byoungwon Choe, Min Gyu Choi, and Hyeong-Seok Ko. 2005. Simulating complex hair with robust collision handling. In Proceedings of the 2005 ACM SIGGRAPH/Eurographics symposium on Computer animation. 153–160.Google ScholarDigital Library
20. David Clyde. 2017. Numerical Subdivision Surfaces for Simulation and Data Driven Modeling of Woven Cloth. Ph.D. Dissertation. UCLA.Google Scholar
21. David Clyde, Joseph Teran, and Rasmus Tamstorf. 2017. Modeling and data-driven parameter estimation for woven fabrics. In Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation. 1–11.Google ScholarDigital Library
22. Peter A Cundall and Otto DL Strack. 1979. A discrete numerical model for granular assemblies. geotechnique 29, 1 (1979), 47–65.Google Scholar
23. Gilles Daviet. 2020. Simple and scalable frictional contacts for thin nodal objects. ACM Trans. Graph. (TOG) 39, 4 (2020), 61–1.Google ScholarDigital Library
24. Gilles Daviet, Florence Bertails-Descoubes, and Laurence Boissieux. 2011. A hybrid iterative solver for robustly capturing coulomb friction in hair dynamics. In Proceedings of the 2011 SIGGRAPH Asia Conference. 1–12.Google ScholarDigital Library
25. Crispin Deul, Tassilo Kugelstadt, Marcel Weiler, and Jan Bender. 2018. Direct position-based solver for stiff rods. In Computer Graphics Forum, Vol. 37. Wiley Online Library, 313–324.Google Scholar
26. Elliot English and Robert Bridson. 2008. Animating developable surfaces using non-conforming elements. In ACM SIGGRAPH 2008 papers. 1–5.Google ScholarDigital Library
27. Yu Fang, Minchen Li, Chenfanfu Jiang, and Danny M Kaufman. 2021. Guaranteed Globally Injective 3D Deformation Processing. ACM Trans. Graph. (TOG) 40, 4 (2021).Google ScholarDigital Library
28. Theodore F Gast, Craig Schroeder, Alexey Stomakhin, Chenfanfu Jiang, and Joseph M Teran. 2015. Optimization integrator for large time steps. IEEE transactions on visualization and computer graphics 21, 10 (2015), 1103–1115.Google ScholarDigital Library
29. Moritz Geilinger, David Hahn, Jonas Zehnder, Moritz Bächer, Bernhard Thomaszewski, and Stelian Coros. 2020. ADD: analytically differentiable dynamics for multi-body systems with frictional contact. ACM Trans. Graph. (TOG) 39, 6 (2020), 1–15.Google ScholarDigital Library
30. Rony Goldenthal, David Harmon, Raanan Fattal, Michel Bercovier, and Eitan Grinspun. 2007. Efficient simulation of inextensible cloth. In ACM SIGGRAPH 2007 papers. 49–es.Google ScholarDigital Library
31. Eitan Grinspun, Anil N Hirani, Mathieu Desbrun, and Peter Schröder. 2003. Discrete shells. In Proceedings of the 2003 ACM SIGGRAPH/Eurographics symposium on Computer animation. Citeseer, 62–67.Google ScholarDigital Library
32. Gaël Guennebaud, Benoît Jacob, et al. 2010. Eigen v3. http://eigen.tuxfamily.org.Google Scholar
33. Qi Guo, Xuchen Han, Chuyuan Fu, Theodore Gast, Rasmus Tamstorf, and Joseph Teran. 2018. A material point method for thin shells with frictional contact. ACM Trans. Graph. (TOG) 37, 4 (2018), 1–15.Google ScholarDigital Library
34. Xuchen Han, Theodore F Gast, Qi Guo, Stephanie Wang, Chenfanfu Jiang, and Joseph Teran. 2019. A hybrid material point method for frictional contact with diverse materials. Proceedings of the ACM on Computer Graphics and Interactive Techniques 2, 2 (2019), 1–24.Google ScholarDigital Library
35. David Harmon, Daniele Panozzo, Olga Sorkine, and Denis Zorin. 2011. Interference-aware geometric modeling. ACM Trans. Graph. (TOG) 30, 6 (2011), 1–10.Google ScholarDigital Library
36. David Harmon, Etienne Vouga, Breannan Smith, Rasmus Tamstorf, and Eitan Grinspun. 2009. Asynchronous contact mechanics. In ACM SIGGRAPH 2009 papers. 1–12.Google ScholarDigital Library
37. David Harmon, Etienne Vouga, Rasmus Tamstorf, and Eitan Grinspun. 2008. Robust treatment of simultaneous collisions. In ACM SIGGRAPH 2008 papers. 1–4.Google ScholarDigital Library
38. R Hauptmann and K Schweizerhof. 1998. A systematic development of ‘solid-shell’element formulations for linear and non-linear analyses employing only displacement degrees of freedom. Int. J. Numer. Methods Eng. 42, 1 (1998), 49–69.Google ScholarCross Ref
39. F Hernandez, G Cirio, AG Perez, and MA Otaduy. 2013. Anisotropic strain limiting. In Proc. of Congreso Español de Informática Gráfica, Vol. 2.Google Scholar
40. Chenfanfu Jiang, Theodore Gast, and Joseph Teran. 2017. Anisotropic elastoplasticity for cloth, knit and hair frictional contact. ACM Trans. Graph. (TOG) 36, 4 (2017).Google ScholarDigital Library
41. Yupeng Jiang, Minchen Li, Chenfanfu Jiang, and Fernando Alonso-Marroquin. 2020. A hybrid material-point spheropolygon-element method for solid and granular material interaction. Int. J. Numer. Methods Eng. (2020).Google ScholarCross Ref
42. Ning Jin, Wenlong Lu, Zhenglin Geng, and Ronald P Fedkiw. 2017. Inequality cloth. In Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation.Google ScholarDigital Library
43. Couro Kane, Jerrold E Marsden, Michael Ortiz, and Matthew West. 2000. Variational integrators and the Newmark algorithm for conservative and dissipative mechanical systems. Int. J. Numer. Methods Eng. 49, 10 (2000), 1295–1325.Google ScholarCross Ref
44. Danny M Kaufman and Dinesh K Pai. 2012. Geometric numerical integration of inequality constrained, nonsmooth Hamiltonian systems. SIAM J. on Sci. Comp. 34, 5 (2012).Google ScholarDigital Library
45. Danny M. Kaufman, Rasmus Tamstorf, Breannan Smith, Jean-Marie Aubry, and Eitan Grinspun. 2014. Adaptive Nonlinearity for Collisions in Complex Rod Assemblies. ACM Trans. on Graphics (SIGGRAPH 2014) (2014).Google Scholar
46. Ted Kim. 2020. A finite element formulation of baraff-witkin cloth. In Symposium on Computer Animation.Google ScholarDigital Library
47. Tassilo Kugelstadt and Elmar Schömer. 2016. Position and orientation based Cosserat rods.. In Symposium on Computer Animation. 169–178.Google Scholar
48. Cheng Li, Min Tang, Ruofeng Tong, Ming Cai, Jieyi Zhao, and Dinesh Manocha. 2020b. P-cloth: interactive complex cloth simulation on multi-GPU systems using dynamic matrix assembly and pipelined implicit integrators. ACM Trans. Graph. (TOG) 39, 6 (2020), 1–15.Google ScholarDigital Library
49. Jie Li, Gilles Daviet, Rahul Narain, Florence Bertails-Descoubes, Matthew Overby, George E Brown, and Laurence Boissieux. 2018a. An implicit frictional contact solver for adaptive cloth simulation. ACM Trans. Graph. (TOG) 37, 4 (2018), 1–15.Google ScholarDigital Library
50. Minchen Li, Zachary Ferguson, Teseo Schneider, Timothy Langlois, Denis Zorin, Daniele Panozzo, Chenfanfu Jiang, and Danny M. Kaufman. 2020a. Incremental Potential Contact: Intersection- and Inversion-free Large Deformation Dynamics. ACM Trans. Graph. 39, 4 (2020).Google ScholarDigital Library
51. Minchen Li, Ming Gao, Timothy Langlois, Chenfanfu Jiang, and Danny M Kaufman. 2019. Decomposed optimization time integrator for large-step elastodynamics. ACM Trans. Graph. (TOG) 38, 4 (2019), 1–10.Google ScholarDigital Library
52. Minchen Li, Alla Sheffer, Eitan Grinspun, and Nicholas Vining. 2018b. FoldSketch: Enriching Garments with Physically Reproducible Folds. ACM Trans. Graph. 37, 4 (2018).Google ScholarDigital Library
53. Junbang Liang, Ming Lin, and Vladlen Koltun. 2019. Differentiable cloth simulation for inverse problems. In Advances in Neural Information Processing Systems. 772–781.Google Scholar
54. Tiantian Liu, Sofien Bouaziz, and Ladislav Kavan. 2017. Quasi-newton methods for real-time simulation of hyperelastic materials. ACM Trans. Graph. (TOG) 36, 3 (2017).Google ScholarDigital Library
55. Libin Lu, Matthew J Morse, Abtin Rahimian, Georg Stadler, and Denis Zorin. 2019. Scalable simulation of realistic volume fraction red blood cell flows through vascular networks. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis. 1–30.Google ScholarDigital Library
56. Yanyan Lu, Zhonghua Xi, and Jyh-Ming Lien. 2014. Collision Prediction: Conservative Advancement Among Obstacles With Unknown Motion. In ASME 2014 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. American Society of Mechanical Engineers Digital Collection.Google Scholar
57. Mickaël Ly, Jean Jouve, Laurence Boissieux, and Florence Bertails-Descoubes. 2020. Projective Dynamics with Dry Frictional Contact. ACM Trans. Graph. (TOG) 39, 4 (2020).Google ScholarDigital Library
58. Miles Macklin, Kenny Erleben, Matthias Müller, Nuttapong Chentanez, Stefan Jeschke, and Tae-Yong Kim. 2020. Primal/dual descent methods for dynamics. In Computer Graphics Forum, Vol. 39. Wiley Online Library, 89–100.Google Scholar
59. Miles Macklin, Matthias Müller, and Nuttapong Chentanez. 2016. XPBD: position-based simulation of compliant constrained dynamics. In Proceedings of the 9th International Conference on Motion in Games. 49–54.Google ScholarDigital Library
60. Sebastian Martin, Peter Kaufmann, Mario Botsch, Eitan Grinspun, and Markus Gross. 2010. Unified simulation of elastic rods, shells, and solids. ACM Trans. Graph. (TOG) 29, 4 (2010), 1–10.Google ScholarDigital Library
61. Aleka McAdams, Andrew Selle, Kelly Ward, Eftychios Sifakis, and Joseph Teran. 2009. Detail preserving continuum simulation of straight hair. ACM Trans. Graph. (TOG) 28, 3 (2009), 1–6.Google ScholarDigital Library
62. Eder Miguel, Derek Bradley, Bernhard Thomaszewski, Bernd Bickel, Wojciech Matusik, Miguel A Otaduy, and Steve Marschner. 2012. Data-driven estimation of cloth simulation models. In Computer Graphics Forum, Vol. 31. Wiley Online Library.Google Scholar
63. Brian Vincent Mirtich. 1996. Impulse-based dynamic simulation of rigid body systems.Google Scholar
64. Matthias Müller, Bruno Heidelberger, Marcus Hennix, and John Ratcliff. 2007. Position based dynamics. Journal of Visual Communication and Image Representation 18, 2 (2007), 109–118.Google ScholarDigital Library
65. Matthias Müller, Tae-Yong Kim, and Nuttapong Chentanez. 2012. Fast simulation of inextensible hair and fur. VRIPHYS 12 (2012), 39–44.Google Scholar
66. Rahul Narain, Armin Samii, and James F O’brien. 2012. Adaptive anisotropic remeshing for cloth simulation. ACM Trans. Graph. (TOG) 31, 6 (2012), 1–10.Google ScholarDigital Library
67. Jorge Nocedal and Stephen Wright. 2006. Numerical optimization.Google Scholar
68. Miguel A Otaduy, Rasmus Tamstorf, Denis Steinemann, and Markus Gross. 2009. Implicit contact handling for deformable objects. In Computer Graphics Forum, Vol. 28. Wiley Online Library, 559–568.Google Scholar
69. Matthew Overby, George E Brown, Jie Li, and Rahul Narain. 2017. ADMM ⊇ Projective Dynamics: Fast Simulation of Hyperelastic Models with Dynamic Constraints. IEEE Transactions on Visualization and Computer Graphics 23, 10 (2017), 2222–2234.Google ScholarDigital Library
70. Željko Penava, Diana Šimić-Penava, and Ž Knezic. 2014. Determination of the elastic constants of plain woven fabrics by a tensile test in various directions. Fibres & Textiles in Eastern Europe (2014).Google Scholar
71. Xavier Provot. 1997. Collision and self-collision handling in cloth model dedicated to design garments. In Computer Animation and Simulation’97. 177–189.Google Scholar
72. Xavier Provot et al. 1995. Deformation constraints in a mass-spring model to describe rigid cloth behaviour. In Graphics interface. Canadian Information Processing Society.Google Scholar
73. Alessio Quaglino. 2012. Membrane locking in discrete shell theories. Ph.D. Dissertation. Georg-August-Universität Göttingen.Google Scholar
74. Stefanie Reese. 2007. A large deformation solid-shell concept based on reduced integration with hourglass stabilization. Int. J. Numer. Methods Eng. 69, 8 (2007).Google ScholarCross Ref
75. Nikolas Schmitt, Martin Knuth, Jan Bender, and Arjan Kuijper. 2013. Multilevel Cloth Simulation using GPU Surface Sampling. VRIPHYS 13 (2013), 1–10.Google Scholar
76. Andrew Selle, Michael Lentine, and Ronald Fedkiw. 2008. A mass spring model for hair simulation. In ACM SIGGRAPH 2008 papers. 1–11.Google ScholarDigital Library
77. Georg Sperl, Rahul Narain, and Chris Wojtan. 2020. Homogenized yarn-level cloth. ACM Trans. Graph. (TOG) 39, 4 (2020), 48–1.Google ScholarDigital Library
78. Jos Stam. 2009. Nucleus: Towards a unified dynamics solver for computer graphics. In 2009 11th IEEE International Conference on Computer-Aided Design and Computer Graphics. IEEE, 1–11.Google ScholarCross Ref
79. Alexey Stomakhin, Russell Howes, Craig Schroeder, and Joseph M Teran. 2012. Energetically consistent invertible elasticity. In Proceedings of the 11th ACM SIGGRAPH/Eurographics conference on Computer Animation. 25–32.Google Scholar
80. Rasmus Tamstorf and Eitan Grinspun. 2013. Discrete bending forces and their Jacobians. Graphical models 75, 6 (2013), 362–370.Google Scholar
81. Rasmus Tamstorf, Toby Jones, and Stephen F McCormick. 2015. Smoothed aggregation multigrid for cloth simulation. ACM Trans. Graph. (TOG) 34, 6 (2015), 1–13.Google ScholarDigital Library
82. Min Tang, Young J Kim, and Dinesh Manocha. 2009. C 2 A: Controlled conservative advancement for continuous collision detection of polygonal models. In 2009 IEEE International Conference on Robotics and Automation. IEEE, 849–854.Google ScholarCross Ref
83. Min Tang, Dinesh Manocha, and Young J Kim. 2013a. Hierarchical and controlled advancement for continuous collision detectionof rigid and articulated models. IEEE transactions on visualization and computer graphics 20, 5 (2013), 755–766.Google Scholar
84. Min Tang, Dinesh Manocha, Sung-Eui Yoon, Peng Du, Jae-Pil Heo, and Ruo-Feng Tong. 2011. VolCCD: Fast continuous collision culling between deforming volume meshes. ACM Trans. Graph. (TOG) 30, 5 (2011), 1–15.Google ScholarDigital Library
85. Min Tang, Ruofeng Tong, Rahul Narain, Chang Meng, and Dinesh Manocha. 2013b. A GPU-based streaming algorithm for high-resolution cloth simulation. In Computer Graphics Forum, Vol. 32. Wiley Online Library, 21–30.Google Scholar
86. Min Tang, Ruofeng Tong, Zhendong Wang, and Dinesh Manocha. 2014. Fast and exact continuous collision detection with bernstein sign classification. ACM Trans. Graph. (TOG) 33, 6 (2014), 1–8.Google ScholarDigital Library
87. Min Tang, Huamin Wang, Le Tang, Ruofeng Tong, and Dinesh Manocha. 2016. CAMA: Contact-aware matrix assembly with unified collision handling for GPU-based cloth simulation. In Computer Graphics Forum, Vol. 35. Wiley Online Library, 511–521.Google Scholar
88. Min Tang, Tongtong Wang, Zhongyuan Liu, Ruofeng Tong, and Dinesh Manocha. 2018. I-cloth: incremental collision handling for GPU-based interactive cloth simulation. ACM Trans. Graph. (TOG) 37, 6 (2018), 1–10.Google ScholarDigital Library
89. Demetri Terzopoulos, John Platt, Alan Barr, and Kurt Fleischer. 1987. Elastically deformable models. In Proceedings of the 14th annual conference on Computer graphics and interactive techniques. 205–214.Google ScholarDigital Library
90. Bernhard Thomaszewski, Simon Pabst, and Wolfgang Strasser. 2009. Continuum-based strain limiting. In Computer Graphics Forum, Vol. 28. Wiley Online Library, 569–576.Google Scholar
91. Nobuyuki Umetani, Danny M Kaufman, Takeo Igarashi, and Eitan Grinspun. 2011. Sensitive couture for interactive garment modeling and editing. ACM Trans. Graph. 30, 4 (2011), 90.Google ScholarDigital Library
92. Pascal Volino and N Magnenat Thalmann. 2000. Implementing fast cloth simulation with collision response. In Proceedings Computer Graphics International 2000. IEEE.Google ScholarCross Ref
93. Huamin Wang, James O’Brien, and Ravi Ramamoorthi. 2010. Multi-resolution isotropic strain limiting. ACM Trans. Graph. (TOG) 29, 6 (2010), 1–10.Google ScholarDigital Library
94. Huamin Wang, James F O’Brien, and Ravi Ramamoorthi. 2011. Data-driven elastic models for cloth: modeling and measurement. ACM Trans. Graph. (TOG) 30, 4 (2011).Google ScholarDigital Library
95. Xinlei Wang, Minchen Li, Yu Fang, Xinxin Zhang, Ming Gao, Min Tang, Danny M Kaufman, and Chenfanfu Jiang. 2020. Hierarchical optimization time integration for cfl-rate mpm stepping. ACM Trans. Graph. (TOG) 39, 3 (2020), 1–16.Google ScholarDigital Library
96. Zhendong Wang, Min Tang, Ruofeng Tong, and Dinesh Manocha. 2015. TightCCD: Efficient and robust continuous collision detection using tight error bounds. In Computer Graphics Forum, Vol. 34. Wiley Online Library, 289–298.Google Scholar
97. Zhendong Wang, Tongtong Wang, Min Tang, and Ruofeng Tong. 2016. Efficient and robust strain limiting and treatment of simultaneous collisions with semidefinite programming. Computational Visual Media 2, 2 (2016), 119–130.Google ScholarCross Ref
98. Zhendong Wang, Longhua Wu, Marco Fratarcangeli, Min Tang, and Huamin Wang. 2018. Parallel Multigrid for Nonlinear Cloth Simulation. Computer Graphics Forum (2018).Google Scholar
99. Kelly Ward and Ming C Lin. 2003. Adaptive grouping and subdivision for simulating hair dynamics. In 11th Pacific Conference onComputer Graphics and Applications, 2003. Proceedings. IEEE, 234–243.Google ScholarCross Ref
100. Nicholas J Weidner, Kyle Piddington, David IW Levin, and Shinjiro Sueda. 2018. Eulerian-on-lagrangian cloth simulation. ACM Trans. Graph. (TOG) 37, 4 (2018), 1–11.Google ScholarDigital Library
101. Zangyueyang Xian, Xin Tong, and Tiantian Liu. 2019. A Scalable Galerkin Multigrid Method for Real-time Simulation of Deformable Objects. ACM Trans. Graph. (TOG) 38, 6 (2019).Google ScholarDigital Library
102. H.T.Y. Yang, S. Saigal, A. Masud, and R.K. Kapania. 2000. A survey of recent shell finite elements. Int. J. Numer. Methods Eng. 47 (2000).Google Scholar
103. Yonghao Yue, Breannan Smith, Peter Yichen Chen, Maytee Chantharayukhonthorn, Ken Kamrin, and Eitan Grinspun. 2018. Hybrid grains: adaptive coupling of discrete and continuum simulations of granular media. ACM Trans. Graph. (TOG) 37, 6 (2018), 1–19.Google ScholarDigital Library
104. Xinyu Zhang, Minkyoung Lee, and Young J Kim. 2006. Interactive continuous collision detection for non-convex polyhedra. The Visual Computer 22, 9 (2006), 749–760.Google ScholarDigital Library
105. Xinyu Zhang, Stephane Redon, Minkyoung Lee, and Young J Kim. 2007. Continuous collision detection for articulated models using taylor models and temporal culling. ACM Trans. Graph. (TOG) 26, 3 (2007), 15–es.Google ScholarDigital Library