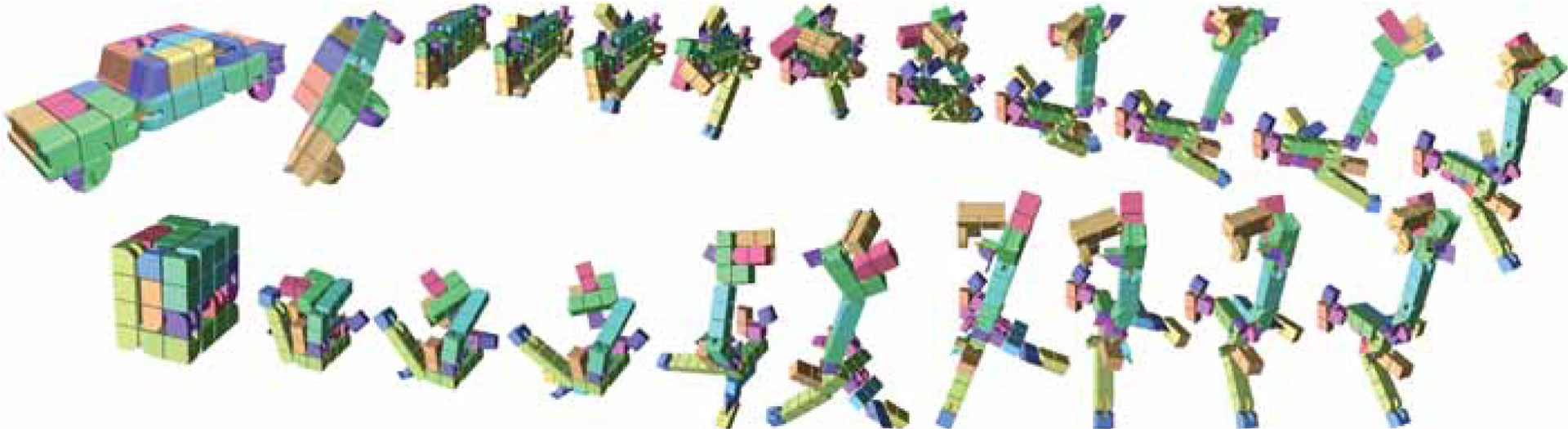
“Boxelization: folding 3D objects into boxes” by Zhou, Sueda, Matusik and Shamir
Conference:
Type(s):
Title:
- Boxelization: folding 3D objects into boxes
Session/Category Title: Games & Design
Presenter(s)/Author(s):
Moderator(s):
Abstract:
We present a method for transforming a 3D object into a cube or a box using a continuous folding sequence. Our method produces a single, connected object that can be physically fabricated and folded from one shape to the other. We segment the object into voxels and search for a voxel-tree that can fold from the input shape to the target shape. This involves three major steps: finding a good voxelization, finding the tree structure that can form the input and target shapes’ configurations, and finding a non-intersecting folding sequence. We demonstrate our results on several input 3D objects and also physically fabricate some using a 3D printer.
References:
1. Abbott, T. G., Abel, Z., Charlton, D., Demaine, E. D., Demaine, M. L., and Kominers, S. D. 2008. Hinged dissections exist. In Proc. 24th Annual Symposium on Computational Geometry, 110–119. Google ScholarDigital Library
2. Alt, H., Knauer, C., Rote, G., and Whitesides, S. 2004. On the complexity of the linkage reconfiguration problem. Contemporary Mathematics 342, 1–14.Google ScholarCross Ref
3. Bächer, M., Bickel, B., James, D. L., and Pfister, H. 2012. Fabricating articulated characters from skinned meshes. ACM Trans. Graph. 31, 4 (July), 47:1–47:9. Google ScholarDigital Library
4. Bächer, M., Whiting, E., Sorkine-Hornung, O., and Bickel, B. 2014. Spin-it: Optimizing moment of inertia for spinnable objects. ACM Trans. Graph. 33, (to appear). Google ScholarDigital Library
5. Berger, B., and Leighton, T. 1998. Protein folding in the hydrophobic-hydrophilic (HP) model is NP-complete. Journal of Computational Biology 5, 1, 27–40.Google ScholarCross Ref
6. Calì, J., Calian, D. A., Amati, C., Kleinberger, R., Steed, A., Kautz, J., and Weyrich, T. 2012. 3D-printing of non-assembly, articulated models. ACM Trans. Graph. 31, 6 (Nov.), 130:1–130:8. Google ScholarDigital Library
7. Chang, H.-H., Lai, Y.-C., Yao, C.-Y., Hua, K.-L., Niu, Y., and Liu, F. 2013. Geometry-shader-based real-time voxelization and applications. The Visual Computer (July), 1–14. Google ScholarDigital Library
8. Chen, X., Golovinskiy, A., and Funkhouser, T. 2009. A benchmark for 3D mesh segmentation. ACM Trans. Graph. 28, 3 (July), 73:1–73:12. Google ScholarDigital Library
9. Chen, D., Sitthi-amorn, P., Lan, J. T., and Matusik, W. 2013. Computing and fabricating multiplanar models. Computer Graphics Forum 32, 2pt3, 305–315.Google Scholar
10. Demaine, E. D., and O’Rourke, J. 2007. Geometric Folding Algorithms: Linkages, Origami, Polyhedra. Cambridge Univ. Press, New York, NY. Google ScholarDigital Library
11. Hildebrand, K., Bickel, B., and Alexa, M. 2012. crdbrd: Shape fabrication by sliding planar slices. Computer Graphics Forum 31, 2pt3, 583–592. Google ScholarDigital Library
12. Istrail, S., and Lam, F. 2009. Combinatorial algorithms for protein folding in lattice models: A survey of mathematical results. Communications in Information and Systems 9, 4, 303.Google ScholarCross Ref
13. Kilian, M., Flöry, S., Chen, Z., Mitra, N. J., Sheffer, A., and Pottmann, H. 2008. Curved folding. ACM Trans. Graph. 27, 3 (Aug.), 75:1–75:9. Google ScholarDigital Library
14. Kirkpatrick, S., Jr., D. G., and Vecchi, M. P. 1983. Optimization by simmulated annealing. Science 220, 4598, 671–680.Google Scholar
15. Lau, M., Ohgawara, A., Mitani, J., and Igarashi, T. 2011. Converting 3D furniture models to fabricatable parts and connectors. ACM Trans. Graph. 30, 4 (July), 85:1–85:6. Google ScholarDigital Library
16. Lazarus, F., and Verroust, A. 1998. 3D metamorphosis: a survey. The Visual Computer 14, 8–9.Google ScholarCross Ref
17. Li, X.-Y., Shen, C.-H., Huang, S.-S., Ju, T., and Hu, S.-M. 2010. Popup: Automatic paper architectures from 3D models. ACM Trans. Graph. 29, 4 (July), 111:1–111:9. Google ScholarDigital Library
18. Li, X.-Y., Ju, T., Gu, Y., and Hu, S.-M. 2011. A geometric study of v-style pop-ups: Theories and algorithms. ACM Trans. Graph. 30, 4 (July), 98:1–98:10. Google ScholarDigital Library
19. Li, H., Alhashim, I., Zhang, H., Shamir, A., and Cohen-Or, D. 2012. Stackabilization. ACM Trans. Graph. 31, 6 (Nov.), 158:1–158:9. Google ScholarDigital Library
20. Lo, K.-Y., Fu, C.-W., and Li, H. 2009. 3D polyomino puzzle. ACM Trans. Graph. 28, 5 (Dec.), 157:1–157:8. Google ScholarDigital Library
21. Loop, C., Zhang, C., and Zhang, Z. 2013. Real-time high-resolution sparse voxelization with application to image-based modeling. In Symposium on High Performance Graphics, 73–79. Google ScholarDigital Library
22. Lowere, B. 1976. The HARPY speech recognition system. Ph.D. Thesis, Carnegie Mellon University. Google ScholarDigital Library
23. Luo, L., Baran, I., Rusinkiewicz, S., and Matusik, W. 2012. Chopper: Partitioning models into 3D-printable parts. ACM Trans. Graph. 31, 6 (Nov.), 129:1–129:9. Google ScholarDigital Library
24. McCrae, J., Singh, K., and Mitra, N. J. 2011. Slices: A shape-proxy based on planar sections. ACM Trans. Graph. 30, 6 (Dec.), 168:1–168:12. Google ScholarDigital Library
25. Mitani, J., and Suzuki, H. 2004. Making papercraft toys from meshes using strip-based approximate unfolding. ACM Trans. Graph. 23, 3 (Aug.), 259–263. Google ScholarDigital Library
26. O’Rourke, J. 2011. How to Fold It: The Mathematics of Linkages, Origami and Polyhedra. Cambridge Univ. Press, New York, NY.Google Scholar
27. Pantaleoni, J. 2011. Voxelpipe: A programmable pipeline for 3D voxelization. In Symposium on High Performance Graphics, 99–106. Google ScholarDigital Library
28. Prévost, R., Whiting, E., Lefebvre, S., and Sorkine-Hornung, O. 2013. Make it stand: Balancing shapes for 3D fabrication. ACM Trans. Graph. 32, 4 (July), 81:1–81:10. Google ScholarDigital Library
29. Schwartzburg, Y., and Pauly, M. 2013. Fabrication-aware design with intersecting planar pieces. Computer Graphics Forum 32, 2pt3, 317–326.Google Scholar
30. Séquin, C. H. 2012. Interactive 3D rapid-prototyping models. In Proc. ACM SIGGRAPH Symposium on Interactive 3D Graphics and Games, 210–210. Google ScholarDigital Library
31. Shamir, A. 2008. A survey on mesh segmentation techniques. Computer Graphics Forum 27, 6, 1539–1556.Google ScholarCross Ref
32. Song, P., Fu, C.-W., and Cohen-Or, D. 2012. Recursive interlocking puzzles. ACM Trans. Graph. 31, 6 (Nov.), 128:1–128:10. Google ScholarDigital Library
33. Tachi, T. 2010. Origamizing polyhedral surfaces. IEEE Transactions on Visualization and Computer Graphics 16, 2, 298–311. Google ScholarDigital Library
34. Transformers, 2007. http://transformersmovie.com.Google Scholar
35. Varadhan, G., Krishnan, S., Kim, Y. J., Diggavi, S., and Manocha, D. 2003. Efficient max-norm distance computation and reliable voxelization. In Symposium on Geometry Processing, 116–126. Google ScholarDigital Library
36. Weeks, D. 2013. Cubebots. http://tweekstudio.com.Google Scholar
37. Wolberg, G. 1998. Image morphing: a survey. The Visual Computer 14, 8, 360–372.Google ScholarCross Ref
38. Xin, S.-Q., Lai, C.-F., Fu, C.-W., Wong, T.-T., He, Y., and Cohen-Or, D. 2011. Making burr puzzles from 3D models. ACM Trans. Graph. 30, 4 (Aug.), 97:1–97:8. Google ScholarDigital Library
39. Zhou, Y., and Wang, R. 2012. An algorithm for creating geometric dissection puzzles. In Proceedings of Bridges 2012: Mathematics, Music, Art, Architecture, Culture, 49–56.Google Scholar