“Box cutter: atlas refinement for efficient packing via void elimination” by Limper, Vining and Sheffer
Conference:
Type(s):
Entry Number: 153
Title:
- Box cutter: atlas refinement for efficient packing via void elimination
Session/Category Title: An Atlas for the World and Other Surfaces
Presenter(s)/Author(s):
Moderator(s):
Abstract:
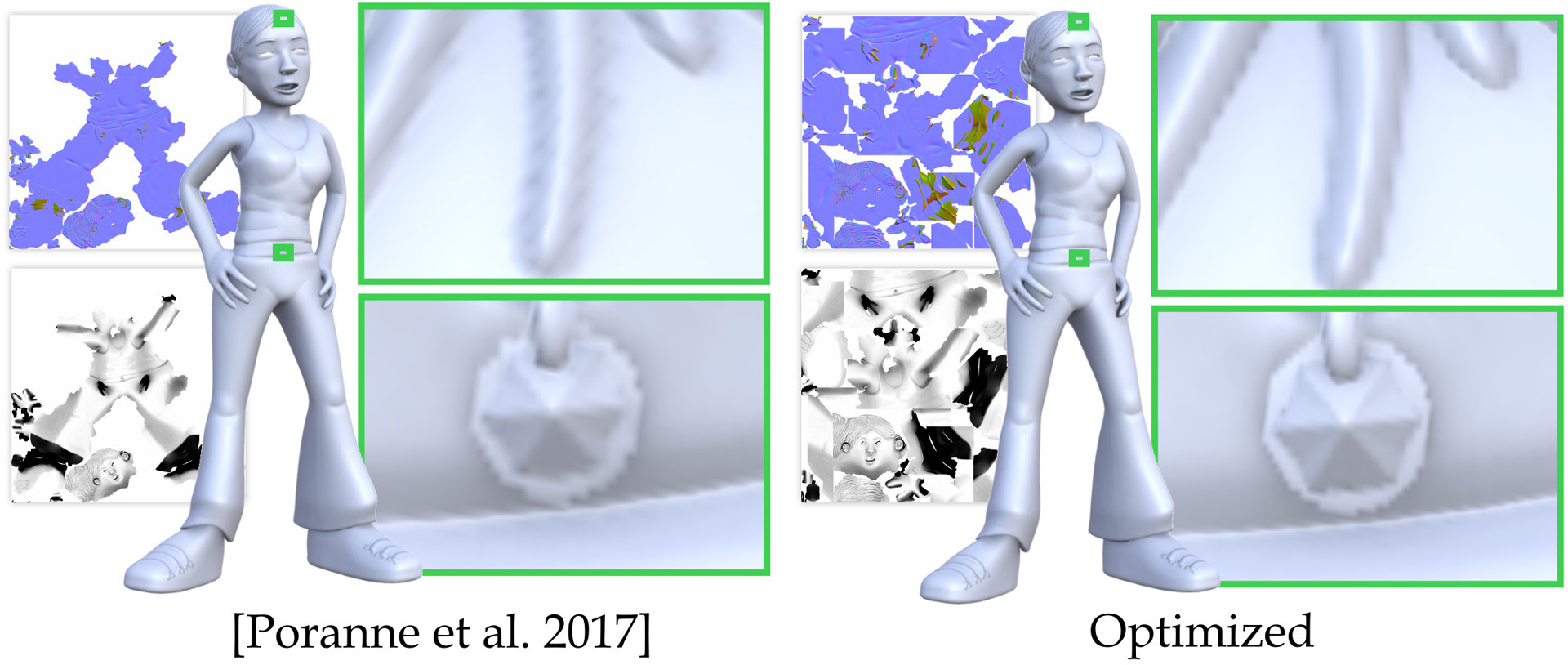
Packed atlases, consisting of 2D parameterized charts, are ubiquitously used to store surface signals such as texture or normals. Tight packing is similarly used to arrange and cut-out 2D panels for fabrication from sheet materials. Packing efficiency, or the ratio between the areas of the packed atlas and its bounding box, significantly impacts downstream applications.We propose Box Cutter, a new method for optimizing packing efficiency suitable for both settings. Our algorithm improves packing efficiency without changing distortion by strategically cutting and repacking the atlas charts or panels. It preserves the local mapping between the 3D surface and the atlas charts and retains global mapping continuity across the newly formed cuts. We balance packing efficiency improvement against increase in chart boundary length and enable users to directly control the acceptable amount of boundary elongation. While the problem we address is NP-hard, we provide an effective practical solution by iteratively detecting large rectangular empty spaces, or void boxes, in the current atlas packing and eliminating them by first refining the atlas using strategically placed axis-aligned cuts and then repacking the refined charts. We repeat this process until no further improvement is possible, or until the desired balance between packing improvement and boundary elongation is achieved. Packed chart atlases are only useful for the applications we address if their charts are overlap-free; yet many popular parameterization methods, used as-is, produce atlases with global overlaps. Our pre-processing step eliminates all input overlaps while explicitly minimizing the boundary length of the resulting overlap-free charts. We demonstrate our combined strategy on a large range of input atlases produced by diverse parameterization methods, as well as on multiple sets of 2D fabrication panels. Our framework dramatically improves the output packing efficiency on all inputs; for instance with boundary length increase capped at 50% we improve packing efficiency by 68% on average.
References:
1. Mirela Ben-Chen, Craig Gotsman, and Guy Bunin. 2008. Conformal Flattening by Curvature Prescription and Metric Scaling. Computer Graphics Forum 27, 2 (2008), 449–458.Google ScholarCross Ref
2. David Bommes, Marcel Campen, Hans-Christian Ebke, Pierre Alliez, and Leif Kobbelt. 2013. Integer-grid Maps for Reliable Quad Meshing. ACM Trans. Graph. 32, 4, Article 98 (July 2013), 12 pages. Google ScholarDigital Library
3. Mario Botsch, Leif Kobbelt, Mark Pauly, Pierre Alliez, and Bruno LÃl’vy. 2010. Polygon Mesh Processing. AK Peters. 250 pages.Google Scholar
4. Alon Bright, Edward Chien, and Ofir Weber. 2017. Harmonic Global Parametrization with Rational Holonomy. ACM Trans. Graph. 36, 4, Article 89 (July 2017), 15 pages. Google ScholarDigital Library
5. Nathan A. Carr and John C. Hart. 2002. Meshed Atlases for Real-time Procedural Solid Texturing. ACM Trans. Graph. 21, 2 (April 2002), 106–131. Google ScholarDigital Library
6. Xuelin Chen, Hao Zhang, Jinjie Lin, Ruizhen Hu, Lin Lu, Qixing Huang, Bedrich Benes, Daniel Cohen-Or, and Baoquan Chen. 2015. Dapper: Decompose-and-pack for 3D Printing. ACM Trans. Graph. 34, 6, Article 213 (Oct. 2015), 12 pages. Google ScholarDigital Library
7. David Cohen-Steiner, Pierre Alliez, and Mathieu Desbrun. 2004. Variational Shape Approximation. In ACM SIGGRAPH 2004 Papers (SIGGRAPH ’04). ACM, New York, NY, USA, 905–914. Google ScholarDigital Library
8. Daniel Sanchez-Crespo Dalmau. 2003. Core Techniques and Algorithms in Game Programming. New Riders Games. Google ScholarDigital Library
9. Michael S. Floater. 1997. Parametrization and Smooth Approximation of Surface Triangulations. Comput. Aided Geom. Des. 14, 3 (April 1997), 231–250. Google ScholarDigital Library
10. Michael R. Garey and David S. Johnson. 1979. Computers and Intractability: A Guide to the Theory of NP-Completeness. W. H. Freeman & Co., New York, NY, USA. Google ScholarDigital Library
11. Francisco González and Gustavo Patow. 2009. Continuity Mapping for Multi-chart Textures. ACM Trans. Graph. 28, 5 (2009), 109:1–109:8. Google ScholarDigital Library
12. Xianfeng Gu, Steven J. Gortler, and Hugues Hoppe. 2002. Geometry Images. In Proceedings of the 29th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH ’02). ACM, New York, NY, USA, 355–361. Google ScholarDigital Library
13. Ziyad S. Hakura and Anoop Gupta. 1997. The Design and Analysis of a Cache Architecture for Texture Mapping. In Proceedings of the 24th Annual International Symposium on Computer Architecture (ISCA ’97). ACM, New York, NY, USA, 108–120. Google ScholarDigital Library
14. K. Hormann, B. Lévy, and A. Sheffer. 2007. Mesh Parameterization: Theory and Practice. In SIGGRAPH 2007 Course Notes. ACM Press, San Diego, CA, vi+115. Google ScholarDigital Library
15. Zhongshi Jiang, Scott Schaefer, and Daniele Panozzo. 2017. Simplicial Complex Augmentation Framework for Bijective Maps. ACM Trans. Graph. 36, 6 (2017), 186:1–186:9. Google ScholarDigital Library
16. M. Jin, Y. Wang, S. T. Yau, and X. Gu. 2004. Optimal global conformal surface parameterization. In IEEE Visualization 2004. 267–274. Google ScholarDigital Library
17. Dan Julius, Vladislav Kraevoy, and Alla Sheffer. 2005. D-Charts: Quasi-Developable Mesh Segmentation. Computer Graphics Forum 24, 3 (2005), 581–590.Google ScholarCross Ref
18. B. W. Kernighan and S. Lin. 1970. An efficient heuristic procedure for partitioning graphs. The Bell System Technical Journal 49, 2 (Feb 1970), 291–307.Google ScholarCross Ref
19. Margret Keuper, Evgeny Levinkov, Nicolas Bonneel, Guillaume Lavoue, Thomas Brox, and Bjorn Andres. 2015. Efficient Decomposition of Image and Mesh Graphs by Lifted Multicuts. In The IEEE International Conference on Computer Vision (ICCV). Google ScholarDigital Library
20. Liliya Kharevych, Boris Springborn, and Peter Schröder. 2006. Discrete Conformal Mappings via Circle Patterns. ACM Trans. Graph. 25, 2 (April 2006), 412–438. Google ScholarDigital Library
21. B. Koo, J. Hergel, S. Lefebvre, and N. J. Mitra. 2017. Towards Zero-Waste Furniture Design. IEEE Transactions on Visualization and Computer Graphics 23, 12 (Dec 2017), 2627–2640.Google ScholarCross Ref
22. Zohar Levi and Denis Zorin. 2014. Strict Minimizers for Geometric Optimization. ACM Trans. Graph. 33, 6, Article 185 (Nov. 2014), 14 pages. Google ScholarDigital Library
23. Bruno Lévy, Sylvain Petitjean, Nicolas Ray, and Jérome Maillot. 2002. Least Squares Conformal Maps for Automatic Texture Atlas Generation. In Proceedings of the 29th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH ’02). ACM, New York, NY, USA, 362–371. Google ScholarDigital Library
24. Yaron Lipman. 2012. Bounded Distortion Mapping Spaces for Triangular Meshes. ACM Trans. Graph. 31, 4, Article 108 (July 2012), 13 pages. Google ScholarDigital Library
25. Songrun Liu, Zachary Ferguson, Alec Jacobson, and Yotam Gingold. 2017. Seamless: Seam erasure and seam-aware decoupling of shape from mesh resolution. ACM Trans. Graph. 36, 6 (2017), 216:1–216:15. Google ScholarDigital Library
26. Victor J. Milenkovic. 1999. Rotational polygon containment and minimum enclosure using only robust 2D constructions. Computational Geometry 13, 1 (1999), 3 — 19. Google ScholarDigital Library
27. Jacob Munkberg, Jon Hasselgren, Petrik Clarberg, Magnus Andersson, and Tomas Akenine-Möller. 2016. Texture Space Caching and Reconstruction for Ray Tracing. ACM Trans. Graph. 35, 6, Article 249 (Nov. 2016), 13 pages. Google ScholarDigital Library
28. Ashish Myles, Nico Pietroni, and Denis Zorin. 2014. Robust Field-aligned Global Parametrization. ACM Trans. Graph. 33, 4, Article 135 (July 2014), 14 pages. Google ScholarDigital Library
29. Ashish Myles and Denis Zorin. 2012. Global parametrization by incremental flattening. ACM Trans. Graph. 31, 4, Article 109 (July 2012), 11 pages. Google ScholarDigital Library
30. Tobias Nöll and Didier Stricker. 2011. Efficient Packing of Arbitrarily Shaped Charts for Automatic Texture Atlas Generation. In Proceedings of the Twenty-second Eurographics Conference on Rendering (EGSR ’11). Eurographics Association, Aire-la-Ville, Switzerland, Switzerland, 1309–1317. Google ScholarDigital Library
31. Roi Poranne, Marco Tarini, Sandro Huber, Daniele Panozzo, and Olga Sorkine-Hornung. 2017. Autocuts: Simultaneous Distortion and Cut Optimization for UV Mapping.Google ScholarDigital Library
32. Budirijanto Purnomo, Jonathan D. Cohen, and Subodh Kumar. 2004. Seamless Texture Atlases. In Proc. Symp. Geometry Processing. 65–74. Google ScholarDigital Library
33. Nicolas Ray, Vincent Nivoliers, Sylvain Lefebvre, and Bruno Lévy. 2010. Invisible Seams. In Proc. Eurographics Conference on Rendering. 1489–1496. Google ScholarDigital Library
34. Pedro V. Sander, Steven J. Gortler, John Snyder, and Hugues Hoppe. 2002. Signal-specialized Parametrization. In Proc. Eurographics Workshop on Rendering. 87–98. Google ScholarDigital Library
35. Pedro V. Sander, John Snyder, Steven J. Gortler, and Hugues Hoppe. 2001. Texture Mapping Progressive Meshes. In Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH ’01). ACM, New York, NY, USA, 409–416. Google ScholarDigital Library
36. P. V. Sander, Z. J. Wood, S. J. Gortler, J. Snyder, and H. Hoppe. 2003. Multi-chart Geometry Images. In Proceedings of the 2003 Eurographics/ACM SIGGRAPH Symposium on Geometry Processing (SGP ’03). Eurographics Association, Aire-la-Ville, Switzerland, Switzerland, 146–155. Google ScholarDigital Library
37. Alla Sheffer and John C. Hart. 2002. Seamster: Inconspicuous Low-distortion Texture Seam Layout. In Proceedings of the Conference on Visualization ’02 (VIS ’02). IEEE Computer Society, Washington, DC, USA, 291–298. Google ScholarDigital Library
38. Alla Sheffer, Bruno Lévy, Maxim Mogilnitsky, and Alexander Bogomyakov. 2005. ABF++: Fast and Robust Angle Based Flattening. ACM Transactions on Graphics (Apr 2005). Google ScholarDigital Library
39. Alla Sheffer, Emil Praun, and Kenneth Rose. 2007. Mesh Parameterization Methods and Their Applications. Foundations and TrendsÃő in Computer Graphics and Vision 2, 2 (2007), 105–171. Google ScholarDigital Library
40. Jason Smith and Scott Schaefer. 2015. Bijective Parameterization with Free Boundaries. ACM Trans. Graph. 34, 4, Article 70 (July 2015), 9 pages. Google ScholarDigital Library
41. Olga Sorkine, Daniel Cohen-Or, Rony Goldenthal, and Dani Lischinski. 2002. Bounded-distortion Piecewise Mesh Parameterization. In Proceedings of the Conference on Visualization ’02 (VIS ’02). IEEE Computer Society, Washington, DC, USA, 355–362. Google ScholarDigital Library
42. Kun Zhou, John Synder, Baining Guo, and Heung-Yeung Shum. 2004. Iso-charts: Stretch-driven Mesh Parameterization Using Spectral Analysis. In Proceedings of the 2004 Eurographics/ACM SIGGRAPH Symposium on Geometry Processing (SGP ’04). ACM, New York, NY, USA, 45–54. Google ScholarDigital Library
43. Yahan Zhou, Shinjiro Sueda, Wojciech Matusik, and Ariel Shamir. 2014. Boxelization: Folding 3D Objects into Boxes. ACM Trans. Graph. 33, 4, Article 71 (July 2014), 8 pages. Google ScholarDigital Library