“Bounded distortion harmonic shape interpolation”
Conference:
Type(s):
Title:
- Bounded distortion harmonic shape interpolation
Session/Category Title: MAPPINGS
Presenter(s)/Author(s):
Moderator(s):
Abstract:
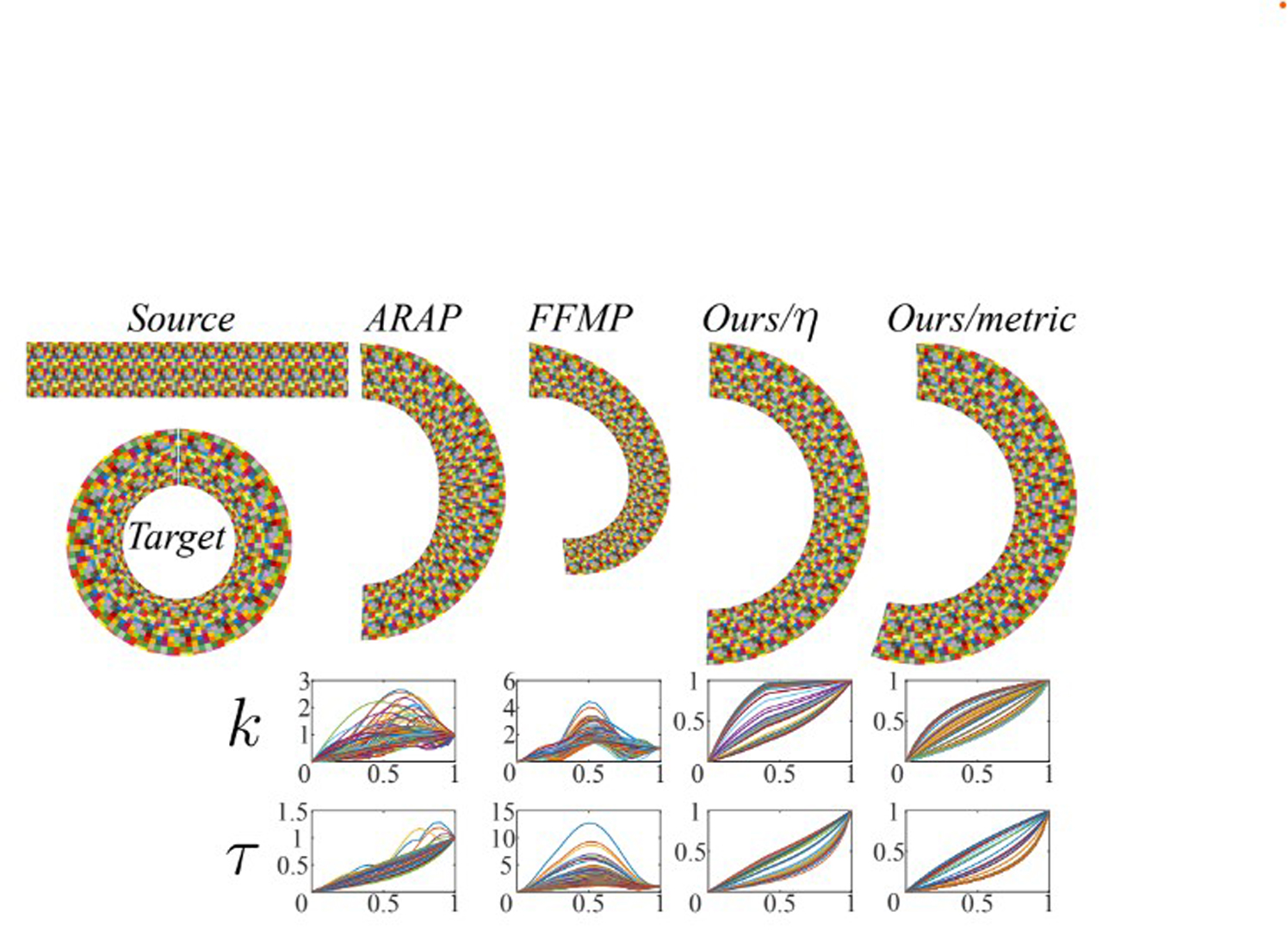
Planar shape interpolation is a classic problem in computer graphics. We present a novel shape interpolation method that blends C∞ planar harmonic mappings represented in closed-form. The intermediate mappings in the blending are guaranteed to be locally injective C∞ harmonic mappings, with conformal and isometric distortion bounded by that of the input mappings. The key to the success of our method is the fact that the blended differentials of our interpolated mapping have a simple closed-form expression, so they can be evaluated with unprecedented efficiency and accuracy. Moreover, in contrast to previous approaches, these differentials are integrable, and result in an actual mapping without further modification. Our algorithm is embarrassingly parallel and is orders of magnitude faster than state-of-the-art methods due to its simplicity, yet it still produces mappings that are superior to those of existing techniques due to its guaranteed bounds on geometric distortion.
References:
1. Ahlfors, L. 1979. Complex analysis, vol. 7. McGraw-Hill Education.Google Scholar
2. Aigerman, N., and Lipman, Y. 2013. Injective and bounded distortion mappings in 3D. ACM Transactions on Graphics (TOG) 32, 4, 106. Google ScholarDigital Library
3. Alexa, M., Cohen-Or, D., and Levin, D. 2000. As-rigid-as-possible shape interpolation. In Proceedings of the 27th annual conference on Computer graphics and interactive techniques, ACM Press/Addison-Wesley Publishing Co., 157–164. Google ScholarDigital Library
4. Alexa, M. 2002. Recent advances in mesh morphing. In Computer graphics forum, vol. 21, Wiley Online Library, 173–198.Google Scholar
5. Baxter, W., Barla, P., and Anjyo, K. 2008. Rigid shape interpolation using normal equations. In Proceedings of the 6th international symposium on Non-photorealistic animation and rendering, ACM, 59–64. Google ScholarDigital Library
6. Bell, S. R. 1992. The Cauchy transform, potential theory and conformal mapping, vol. 7. CRC press.Google Scholar
7. Chen, R., and Weber, O. 2015. Bounded distortion harmonic mappings in the plane. ACM Transactions on Graphics (TOG) 34, 4, 73. Google ScholarDigital Library
8. Chen, R., Weber, O., Keren, D., and Ben-Chen, M. 2013. Planar shape interpolation with bounded distortion. ACM Transactions on Graphics (TOG) 32, 4, 108. Google ScholarDigital Library
9. Choi, J., and Szymczak, A. 2003. On coherent rotation angles for as-rigid-as-possible shape interpolation. In Proceedings of the 15th Canadian Conference on Computational Geometry, 111–114.Google Scholar
10. Duren, P. 2004. Harmonic mappings in the plane. Cambridge University Press.Google Scholar
11. Kircher, S., and Garland, M. 2008. Free-form motion processing. ACM Transactions on Graphics (TOG) 27, 2, 12. Google ScholarDigital Library
12. Knöppel, F., Crane, K., Pinkall, U., and Schröder, P. 2013. Globally optimal direction fields. ACM Transactions on Graphics (TOG) 32, 4, 59. Google ScholarDigital Library
13. Kovalsky, S. Z., Aigerman, N., Basri, R., and Lipman, Y. 2014. Controlling singular values with semidefinite programming. ACM Transactions on Graphics (TOG), 4. Google ScholarDigital Library
14. Kovalsky, S. Z., Aigerman, N., Basri, R., and Lipman, Y. 2015. Large-scale bounded distortion mappings. ACM Transactions on Graphics (TOG) 34, 6, 191. Google ScholarDigital Library
15. Levi, Z., and Weber, O. 2016. On the convexity and feasibility of the bounded distortion harmonic mapping problem. ACM TOG 35, 4. Google ScholarDigital Library
16. Levi, Z., and Zorin, D. 2014. Strict minimizers for geometric optimization. ACM Transactions on Graphics (TOG) 33, 6, 185. Google ScholarDigital Library
17. Lipman, Y. 2012. Bounded distortion mapping spaces for triangular meshes. ACM Transactions on Graphics (TOG) 31, 4, 108. Google ScholarDigital Library
18. Poranne, R., and Lipman, Y. 2014. Provably good planar mappings. ACM Transactions on Graphics (TOG) 33, 4, 76. Google ScholarDigital Library
19. Schüller, C., Kavan, L., Panozzo, D., and Sorkine-Hornung, O. 2013. Locally injective mappings. In Computer Graphics Forum, vol. 32, Wiley Online Library, 125–135. Google ScholarDigital Library
20. Surazhsky, V., and Gotsman, C. 2001. Controllable morphing of compatible planar triangulations. ACM Transactions on Graphics 20, 4, 203–231. Google ScholarDigital Library
21. Surazhsky, V., and Gotsman, C. 2003. Intrinsic morphing of compatible triangulations. International Journal of Shape Modeling 9, 02, 191–201.Google ScholarCross Ref
22. Tutte, W. 1963. How to draw a graph. Proc. London Math. Soc 13, 3, 743–768.Google ScholarCross Ref
23. Weber, O., and Gotsman, C. 2010. Controllable conformal maps for shape deformation and interpolation. ACM Transactions on Graphics (TOG) 29, 4, 78. Google ScholarDigital Library
24. Weber, O., and Zorin, D. 2014. Locally injective parametrization with arbitrary fixed boundaries. ACM Transactions on Graphics (TOG) 33, 4, 75. Google ScholarDigital Library
25. Weber, O., Sorkine, O., Lipman, Y., and Gotsman, C. 2007. Context-aware skeletal shape deformation. In Computer Graphics Forum, vol. 26, Wiley Online Library, 265–274.Google Scholar
26. Weber, O., Ben-Chen, M., and Gotsman, C. 2009. Complex barycentric coordinates with applications to planar shape deformation. Computer Graphics Forum 28, 2, 587–597.Google ScholarCross Ref
27. Weber, O., Myles, A., and Zorin, D. 2012. Computing extremal quasiconformal maps. Computer Graphics Forum 31, 5, 1679–1689. Google ScholarDigital Library
28. Wolberg, G. 1998. Image morphing: a survey. The visual computer 14, 8, 360–372.Google Scholar
29. Xu, D., Zhang, H., Wang, Q., and Bao, H. 2006. Poisson shape interpolation. Graphical models 68, 3, 268–281. Google ScholarDigital Library