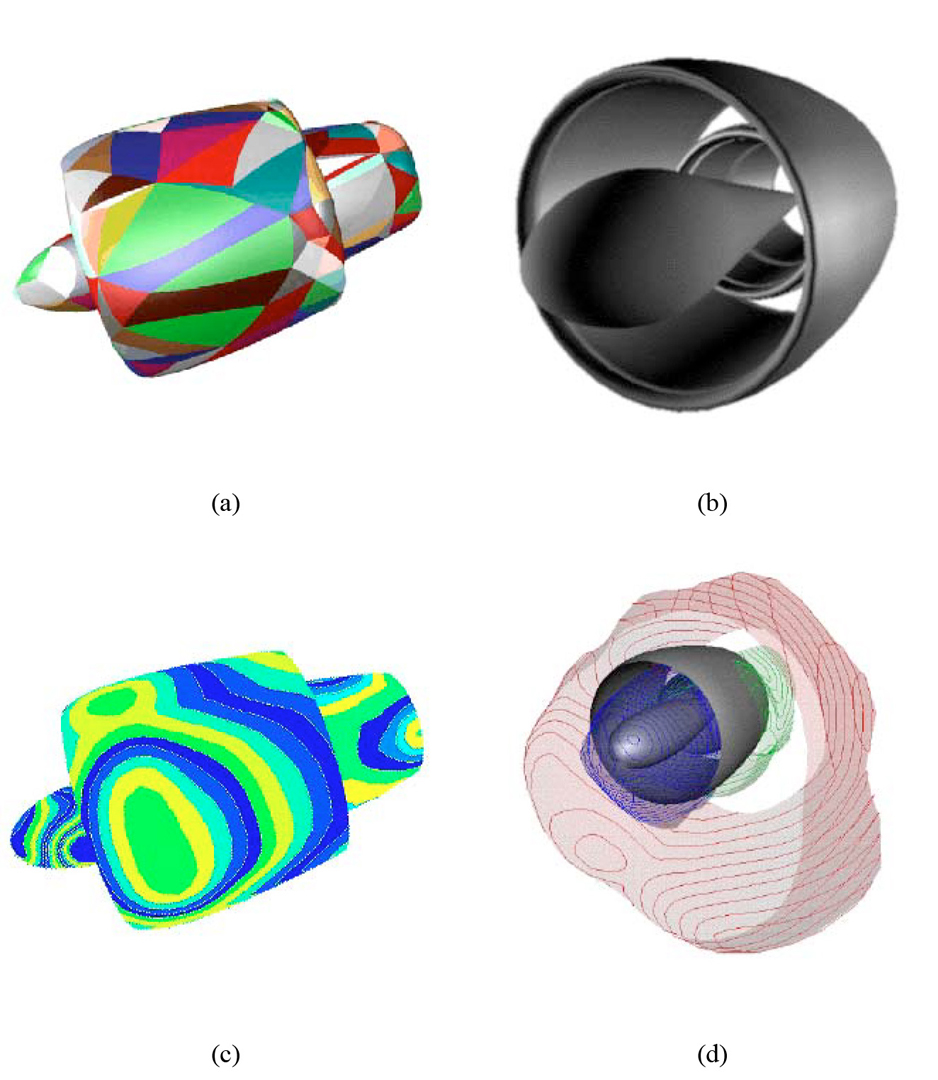
“Automatic reconstruction of surfaces and scalar fields from 3D scans” by Bajaj, Bernardini and Xu

We present an efficient and uniform approach for the automatic reconstruction of surfaces of CAD (computer aided design) models and scalar fields defined on them, from an unorganized collection of scanned point data. A possible application is the rapid computer model reconstruction of an existing part or prototype from a three dimensional (3D) points scan of its surface. Color, texture or some scalar material property of the physical part, define natural scalar fields over the surface of the CAD model. Our reconstruction algorithm does not impose any convexity or differentiability restrictions on the surface of the original physical part or the scalar field function, except that it assumes that there is a sufficient sampling of the input point data to unambiguously reconstruct the CAD model. Compared to earlier methods our algorithm has the advantages of simplicity, efficiency and uniformity (both CAD model and scalar field reconstruction). The simplicity and efficiency of our approach is based on several novel uses of appropriate sub-structures (alpha shapes) of a three-dimensional Delaunay Triangulation, its dual the three-dimensional Voronoi diagram, and dual uses of trivariate Bernstein-Bézier forms. The boundary of the CAD model is modeled using implicit cubic Bernstein-Bézier patches, while the scalar field is reconstructed with functional cubic Bernstein-Bézier patches.

1. ALFELD, P. A trivariate clough-tocher scheme for tetrahedral data. Computer Aided Geometric Design i (1984), 169-181.
2. ALFELD, P. Scattered data interpolation in three or more variables. In Mathematical Methods in Computer Aided Geometric Design, T. Lyche and L. Schumaker, Eds. Academic Press, Boston, 1989, pp. 1-34.
3. AURENHAMMER, F. Power diagrams: properties, algorithms and applications. SIAM J. Comput. i6 (1987), 78-96.
4. BAJAJ, C., BERNARDINI, F., AND XU, G. Reconstruction of surfaces and surfaces-on-surfaces from unorganized weighted points. Computer Science Technical Report CSD-TR-94-001, Purdue University, 1994.
5. BAJAJ, C., BERNARDINI, F., AND XU, G. Adaptive reconstruction of surfaces and scalar fields from dense scattered trivariate data. Computer Science Technical Report CSD-TR-95-028, Purdue University, 1995.
6. BAJAJ, C., CHEN, J., AND XU, G. Modeling with cubic A- patches. ACM Transactions on Graphics (1995). To Appear.
7. BAJAJ, C., AND IHM, I. C1 smoothing of polyhedra with implicit algebraic splines. Computer Graphics 26, 2 (July 1992), 79-88. Proceedings of SIGGRAPH 92.
8. BAJAJ, C., AND XU, G. Modeling scattered function data on curved surfaces. In Fundamentals of Computer Graphics, Z. T. J. Chen, N. Thalmann and D. Thalmann, Eds. Beijing, China, 1994, pp. 19-29.
9. BARNHILL, R. E. Surfaces in computer aided geometric design: A survey with new results. Computer Aided Geometric Design 2 (1985), 1-17.
10. BARNHILL, R. E., AND FOLEY, T. A. Methods for constructing surfaces on surfaces. In Geometric Modeling: Methods and their Applications, G. Farin, Ed. Springer, Berlin, 1991, pp. 1- 15.
11. BARNHILL, R. E., OPITZ, K., AND POTTMANN, H. Fat surfaces: a trivariate approach to triangle-based interpolation on surfaces. Computer Aided Geometric Design 9 (1992), 365- 378.
12. BARNHILL, R. E., PIPER, B. R., AND RESCORLA, K. L. Interpolation to arbitrary data on a surface. In Geometric Modeling, G. Farin, Ed. SIAM, Philadelphia, 1987, pp. 281-289.
13. BOISSONAT, J. D. Geometric structures for three-dimensional shape representation. ACM Transactions on Graphics 3, 4 (Oct. 1984), 266-286.
14. CLARKSON, K. L. A randomized algorithm for closest-point queries. SIAM J. Comput. 17 (1988), 830-847.
15. DAHMEN, W. Smooth piecewise quadratic surfaces. In Mathematical Methods in Computer Aided Geometric Design, T. Lyche and L. Schumaker, Eds. Academic Press, Boston, 1989, pp. 181-193.
16. DAHMEN, W., AND THAMM-SCHAAR, T.-M. Cubicoids: modeling and visualization. Computer Aided Geometric Design 10 (1993), 93-108.
17. DEY, T. K., BAJAJ, C. L., AND SUGIHARA, K. On good triangulations in three dimensions. Internat. J. Comput. Geom. Appl. 2, 1 (1992), 75-95.
18. DEY, T. K., SUGIHARA, K., AND BAJAJ, C. L. Delaunay triangulations in three dimensions with finite precision arithmetic. Comput. Aided Geom. Design 9 (1992), 457-470.
19. EDELSBRUNNER, H. Algorithms in Combinatorial Geometry, vol. 10 of EATCS Monographs on Theoretical Computer Science. Springer-Verlag, Heidelberg, West Germany, 1987.
20. EDELSBRUNNER, H., KIRKPATRICK, D., AND SEIDEL, R. On the shape of a set of points in the plane. IEEE Trans. on Information Theory 29, 4 (1983), 551-559.
21. EDELSBRUNNER, H., AND MUCKE, E. E Three-dimensional alpha shapes. ACM Transactions on Graphics 13, 1 (Jan. 1994), 43-72.
22. EDELSBRUNNER, H., AND SHAH, N. R. Incremental topological flipping works for regular triangulations. In Proc. 8th Annu. ACM Sympos. Comput. Geom. (1992), pp. 43-52.
23. FARIN, G. Triangular Bemstein-B6zier patches. Computer Aided Geometric Design 3 (1986), 83-127.
24. FARIN, G. Curves and Sulfaces forComputerAided Geometric Design: A Practical Guide. Academic Press, 1990.
25. FAUGERAS, O. D., HEBERT, M., MUSSI, P., AND BOISSONNAT, J. D. Polyhedral approximation of 3-D objects without holes. Computer Vision, Graphics and Image Processing 25 (1984), 169-183.
26. FRANKE, R. Recent advances in the approximation of surfaces from scattered data. In Multivariate Approximation, C.K.Chui, L.L.Schumarker, and F.I.Utreras, Eds. Academic Press, New York, 1987, pp. 275-335.
27. Guo, B. Surface generation using implicit cubics. In Scientific Visualizaton of Physical Phenomena, N. M. Patrikalakis, Ed. Springer-Verlag, Tokyo, 1991, pp. 485-530.
28. Guo, B. Non-splitting macro patches for implicit cubic spline surfaces. Computer Graphics Forum 12, 3 (1993), 434-445.
29. HOPPE, H., DEROSE, f., DUCHAMP, f., HALSTEAD, M., JIN, n., MCDONALD, J., SCHWITZER, J., AND STUELZLE, W. Piecewise smooth surface reconstruction. In Computer Graphics Proceedings (1994), Annual Conference Series. Proceedings of SIGGRAPH 94, ACM SIGGRAPH, pp. 295-302.
30. HOPPE, H., DEROSE, T., DUCHAMP, T., MCDONALD, J., AND STUELZLE, W. Surface reconstruction from unorganized points. Computer Graphics 26, 2 (July 1992), 71-78. Proceedings of SIGGRAPH 92.
31. HOPPE, n., DEROSE, T., DUCHAMP, f., MCDONALD, J., AND STUELZLE, W. Mesh optimization. In Computer Graphics Proceedings (1993), Annual Conference Series. Proceedings of SIGGRAPH 93, ACM SIGGRAPH, pp. 19-26.
32. MOORE, D., AND WARREN, J. Approximation of dense scattered data using algebraic surfaces. In Proceedings of the 24th annual Hawaii International Conference on System Sciences (1991), V. Milutinovic and B. D. Shriver, Eds., vol. 1.
33. NIELSON, G. M. Modeling and visualizing volumetric and surface-on-surface data. In Focus on Scientific Visualization, H. Hagen, H. Muller, and G. M. Nielson, Eds. Springer, 1992, pp. 219-274.
34. NIELSON, G. M. Scattered data modeling. IEEE Computer Graphics & Applications 13 (1993), 60-70.
35. NIELSON, G. M., FOLEY, T., LANE, D., FRANKE, R., AND HAGEN, H. Interpolation of scattered data on closed surfaces. Computer Aided Geometric Design 7, 4 (1990), 303-312.
36. NIELSON, G. M., FOLEY, T. A., HAMANN, B., AND LANE, D. Visualizing and modeling scattered multivariate data. IEEE Computer Graphics & Applications 11, 3 (May 1991), 47-55.
37. NIELSON, G. M., AND FRANKE, R. Scattered data interpolation and applications: A tutorial and survey. In Geometric Modeling: Methods and Their Applications, H. Hagen and D. Roller, Eds. Springer, 1990, pp. 131-160.
38. O’ROURKE, J. Polyhedra ofminimal area as 3D object models. In Proc. of the International Joint Conference on Artificial Intelligence (1981), pp. 664-666.
39. POTTMANN, H. Interpolation on surfaces using minimum norm networks. Computer Aided Geometric Design 9 (1992), 51- 67.
40. PREPARATA, F. P., AND SHAMOS, M. I. Computational Geometry: an Introduction. Springer-Verlag, New York, NY, 1985.
41. RESCORLA, K. C~ trivariate polynomial interpolation. Computer Aided Geometric Design 4 (1987), 237-244.
42. TURK, G., AND LEVOY, M. Zippered polygonal meshes from range images. In Computer Graphics Proceedings (1994), Annual Conference Series. Proceedings of SIGGRAPH 94, ACM SIGGRAPH, pp. 311-318.
43. VELTKAMP, R. C. 3D computational morphology. Computer Graphics Forum 12, 3 (1993), 115-127.
44. WORSEY, A., AND FARIN, G. An n-dimensional clough-tocher interpolant. Constructive Approximation 3, 2 (1987), 99-110.