“Antithetic sampling for Monte Carlo differentiable rendering” by Zhang, Dong, Doggett and Zhao

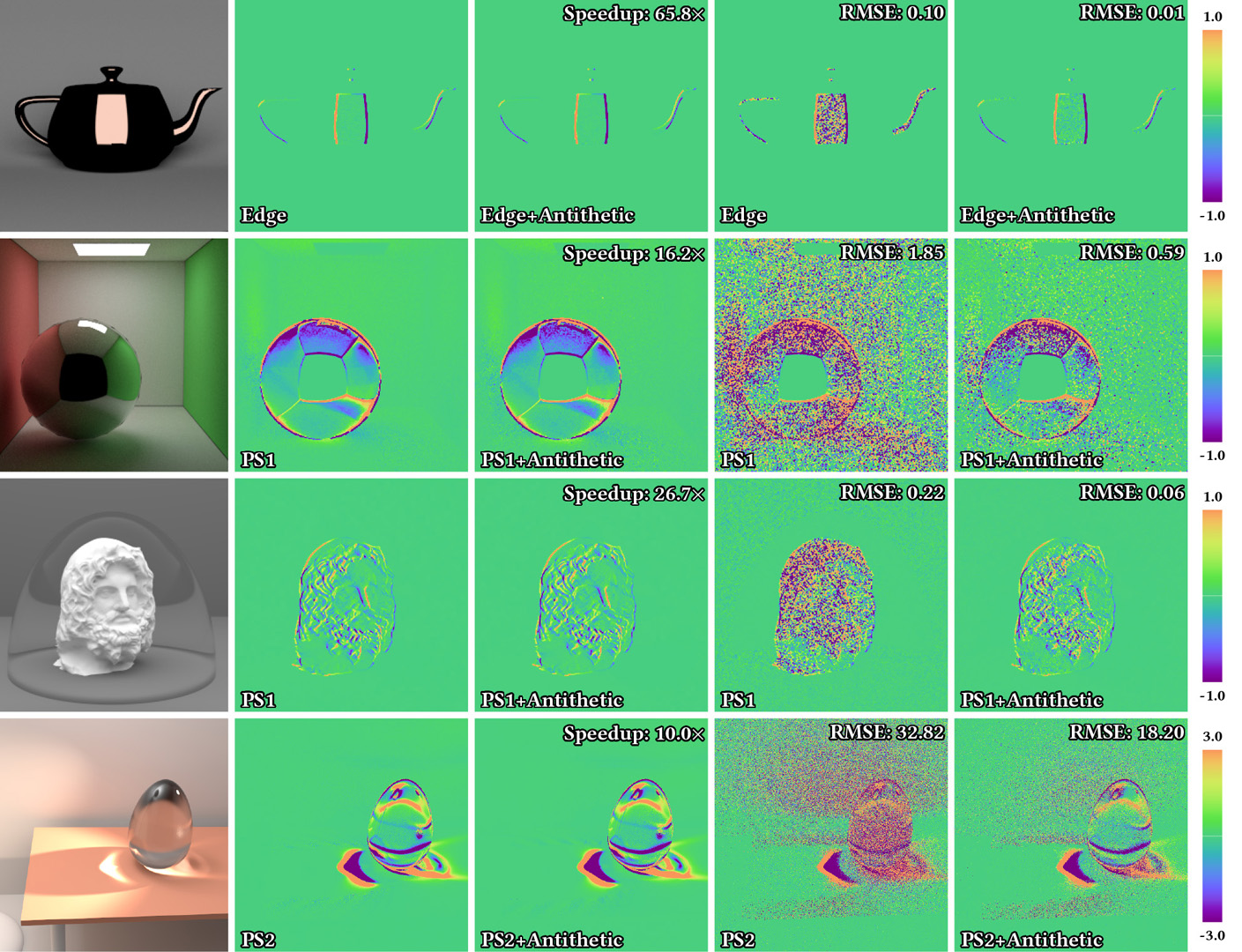
Stochastic sampling of light transport paths is key to Monte Carlo forward rendering, and previous studies have led to mature techniques capable of drawing high-contribution light paths in complex scenes. These sampling techniques have also been applied to differentiable rendering.In this paper, we demonstrate that path sampling techniques developed for forward rendering can become inefficient for differentiable rendering of glossy materials—especially when estimating derivatives with respect to global scene geometries. To address this problem, we introduce antithetic sampling of BSDFs and light-transport paths, allowing significantly faster convergence and can be easily integrated into existing differentiable rendering pipelines. We validate our method by comparing our derivative estimates to those generated with existing unbiased techniques. Further, we demonstrate the effectiveness of our technique by providing equal-quality and equal-time comparisons with existing sampling methods.

1. Michael Ashikhmin and Peter Shirley. 2000. An anisotropic phong BRDF model. Journal of graphics tools 5, 2 (2000), 25–32.Google ScholarDigital Library
2. Sai Bangaru, Tzu-Mao Li, and Frédo Durand. 2020. Unbiased warped-area sampling for differentiable rendering. ACM Trans. Graph. 39, 6 (2020), 245:1–245:18.Google ScholarDigital Library
3. Robert L Cook and Kenneth E. Torrance. 1982. A reflectance model for computer graphics. ACM Transactions on Graphics (ToG) 1, 1 (1982), 7–24.Google ScholarDigital Library
4. John Geweke. 1988. Antithetic acceleration of Monte Carlo integration in Bayesian inference. Journal of Econometrics 38, 1–2 (1988), 73–89.Google ScholarCross Ref
5. John Michael Hammersley and JG Mauldon. 1956. General principles of antithetic variates. In Mathematical proceedings of the Cambridge philosophical society, Vol. 52. Cambridge University Press, 476–481.Google Scholar
6. Eric Heitz and Eugene d’Eon. 2014. Importance sampling microfacet-based BSDFs using the distribution of visible normals. In Computer Graphics Forum, Vol. 33. Wiley Online Library, 103–112.Google Scholar
7. Eric Heitz, Johannes Hanika, Eugene d’Eon, and Carsten Dachsbacher. 2016. Multiple-scattering microfacet BSDFs with the Smith model. ACM Trans. Graph. 35, 4 (2016), 58:1–58:14.Google ScholarDigital Library
8. Csaba Kelemen and Laszlo Szirmay-Kalos. 2001. A microfacet based coupled specular-matte BRDF model with importance sampling. In Eurographics short presentations, Vol. 2. 4.Google Scholar
9. Markus Kettunen, Marco Manzi, Miika Aittala, Jaakko Lehtinen, Frédo Durand, and Matthias Zwicker. 2015. Gradient-domain path tracing. ACM Trans. Graph. 34, 4 (2015), 123:1–123:13 pages.Google ScholarDigital Library
10. Diederik P Kingma and Jimmy Ba. 2014. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980 (2014).Google Scholar
11. Joo Ho Lee, Adrian Jarabo, Daniel S. Jeon, Diego Gutierrez, and Min H. Kim. 2018. Practical multiple scattering for rough surfaces. ACM Trans. Graph. 37, 6 (2018), 275:1–275:12.Google ScholarDigital Library
12. Tzu-Mao Li, Miika Aittala, Frédo Durand, and Jaakko Lehtinen. 2018. Differentiable Monte Carlo ray tracing through edge sampling. ACM Trans. Graph. 37, 6 (2018), 222:1–222:11.Google ScholarDigital Library
13. Guillaume Loubet, Nicolas Holzschuch, and Wenzel Jakob. 2019. Reparameterizing discontinuous integrands for differentiable rendering. ACM Transactions on Graphics (TOG) 38, 6 (2019), 1–14.Google ScholarDigital Library
14. Morgan McGuire. 2017. Computer graphics archive. https://casual-effects.com/dataGoogle Scholar
15. Merlin Nimier-David, Delio Vicini, Tizian Zeltner, and Wenzel Jakob. 2019. Mitsuba 2: a retargetable forward and inverse renderer. ACM Transactions on Graphics (TOG) 38, 6 (2019), 203.Google ScholarDigital Library
16. Michael Oren and Shree K Nayar. 1994. Generalization of Lambert’s reflectance model. In Proceedings of the 21st annual conference on Computer graphics and interactive techniques. 239–246.Google ScholarDigital Library
17. A. Cengiz Öztireli. 2016. Integration with stochastic point processes. ACM Trans. Graph. 35, 5 (2016), 160:1–160:16.Google ScholarDigital Library
18. Bui Tuong Phong. 1975. Illumination for computer generated pictures. Commun. ACM 18, 6 (1975), 311–317.Google ScholarDigital Library
19. Sylvia C Pont and Jan J Koenderink. 2002. Bidirectional reflectance distribution function of specular surfaces with hemispherical pits. JOSA A 19, 12 (2002), 2456–2466.Google ScholarCross Ref
20. Hongyu Ren, Shengjia Zhao, and Stefano Ermon. 2019. Adaptive antithetic sampling for variance reduction. In International Conference on Machine Learning. PMLR, 5420–5428.Google Scholar
21. Christophe Schlick. 1994. An inexpensive BRDF model for physically-based rendering. In Computer graphics forum, Vol. 13. Wiley Online Library, 233–246.Google Scholar
22. Gurprit Singh, Kartic Subr, David Coeurjolly, Victor Ostromoukhov, and Wojciech Jarosz. 2020. Fourier analysis of correlated Monte Carlo importance sampling. Computer Graphics Forum 39, 1 (2020), 7–19.Google ScholarCross Ref
23. Gurprit Singh, Cengiz Öztireli, Abdalla G.M. Ahmed, David Coeurjolly, Kartic Subr, Oliver Deussen, Victor Ostromoukhov, Ravi Ramamoorthi, and Wojciech Jarosz. 2019. Analysis of sample correlations for Monte Carlo rendering. Computer Graphics Forum 38, 2 (2019), 473–491.Google ScholarCross Ref
24. Kartic Subr, Derek Nowrouzezahrai, Wojciech Jarosz, Jan Kautz, and Kenny Mitchell. 2014. Error analysis of estimators that use combinations of stochastic sampling strategies for direct illumination. Computer Graphics Forum 33, 4 (2014), 93–102.Google ScholarCross Ref
25. Orren Jack Turner. 1947. Einstein in 1947. https://commons.wikimedia.org/wiki/File:Albert_Einstein_Head.jpgGoogle Scholar
26. Bram van Ginneken, Marigo Stavridi, and Jan J Koenderink. 1998. Diffuse and specular reflectance from rough surfaces. Applied optics 37, 1 (1998), 130–139.Google Scholar
27. Bruce Walter, Stephen R Marschner, Hongsong Li, and Kenneth E Torrance. 2007. Microfacet models for refraction through rough surfaces. Rendering techniques 2007 (2007), 18th.Google Scholar
28. Gregory J Ward. 1992. Measuring and modeling anisotropic reflection. In Proceedings of the 19th annual conference on Computer graphics and interactive techniques. 265–272.Google ScholarDigital Library
29. Mike Wu, Noah Goodman, and Stefano Ermon. 2019. Differentiable antithetic sampling for variance reduction in stochastic variational inference. In The 22nd International Conference on Artificial Intelligence and Statistics. PMLR, 2877–2886.Google Scholar
30. Feng Xie and Pat Hanrahan. 2018. Multiple scattering from distributions of specular V-grooves. ACM Trans. Graph. 37, 6 (2018), 276:1–2767:14.Google ScholarDigital Library
31. Cheng Zhang, Bailey Miller, Kai Yan, Ioannis Gkioulekas, and Shuang Zhao. 2020. Path-space differentiable rendering. ACM Trans. Graph. 39, 4 (2020), 143:1–143:19.Google ScholarDigital Library
32. Cheng Zhang, Lifan Wu, Changxi Zheng, Ioannis Gkioulekas, Ravi Ramamoorthi, and Shaung Zhao. 2019. A differential theory of radiative transfer. ACM Trans. Graph. 38, 6 (2019), 227:1–227:16.Google ScholarDigital Library
33. Shuang Zhao, Wenzel Jakob, and Tzu-Mao Li. 2020. Physics-based differentiable rendering: a comprehensive introduction. In ACM SIGGRAPH 2020 Courses. 14:1–14:30.Google ScholarDigital Library