“Anisotropic polygonal remeshing” by Alliez, Cohen-Steiner, Devillers, Levy and Desbrun

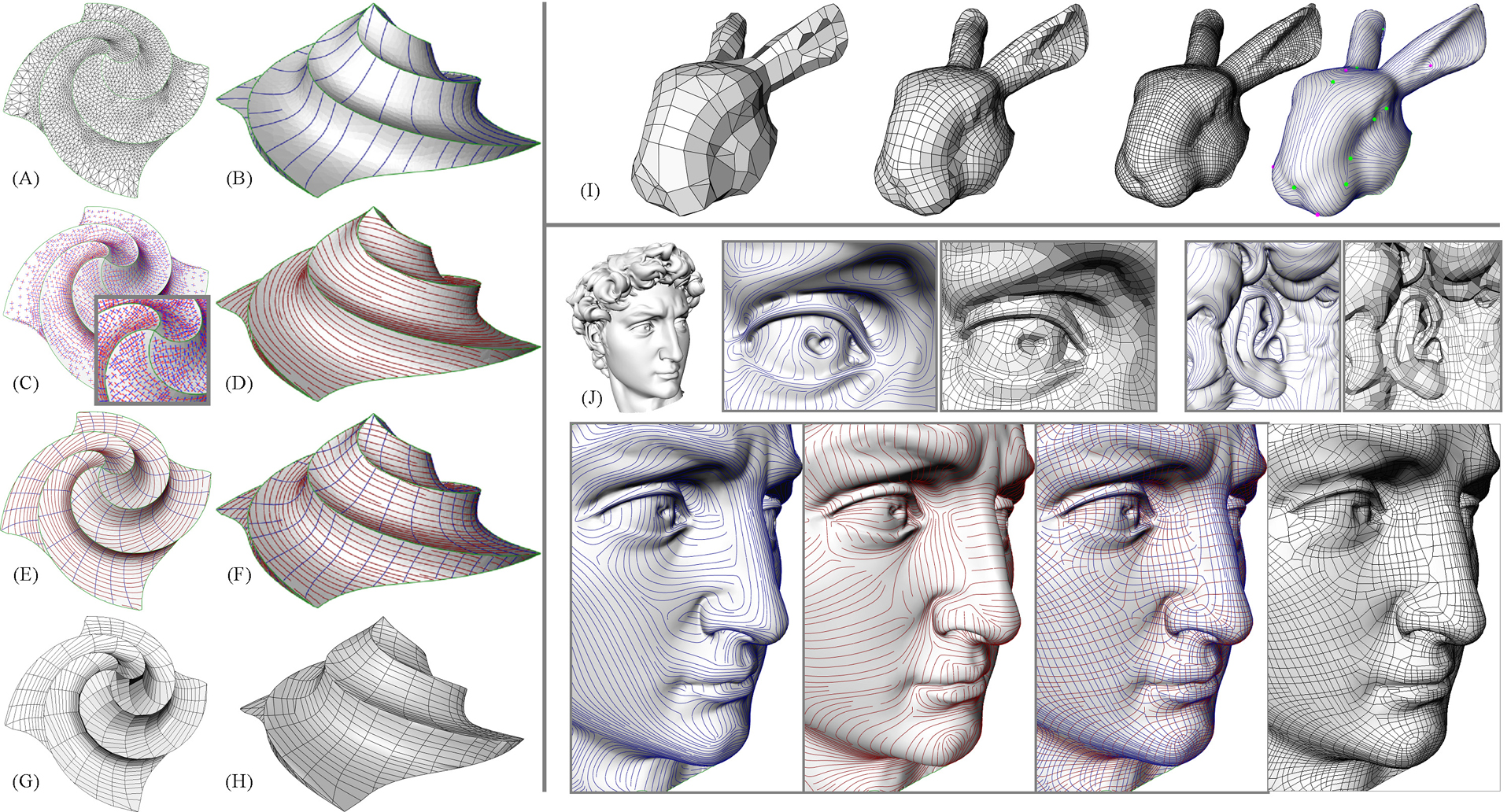
In this paper, we propose a novel polygonal remeshing technique that exploits a key aspect of surfaces: the intrinsic anisotropy of natural or man-made geometry. In particular, we use curvature directions to drive the remeshing process, mimicking the lines that artists themselves would use when creating 3D models from scratch. After extracting and smoothing the curvature tensor field of an input genus-0 surface patch, lines of minimum and maximum curvatures are used to determine appropriate edges for the remeshed version in anisotropic regions, while spherical regions are simply point sampled since there is no natural direction of symmetry locally. As a result our technique generates polygon meshes mainly composed of quads in anisotropic regions, and of triangles in spherical regions. Our approach provides the flexibility to produce meshes ranging from isotropic to anisotropic, from coarse to dense, and from uniform to curvature adapted.

1. ALLIEZ, P., MEYER, M., AND DESBRUN, M. 2002. Interactive Geometry Remeshing. ACM Transactions on Graphics 21 (3), 347–354. ACM SIGGRAPH conference proceedings.]] Google ScholarDigital Library
2. ALLIEZ, P., COLIN DE VERDIÈRE, É., DEVILLERS, O., AND ISENBURG, M. 2003. Isotropic Surface Remeshing. In Shape Modeling International Conference Proceedings. To appear.]] Google Scholar
3. BOROUCHAKI, H., AND FREY, P. 1998. Adaptive Triangular-Quadrilateral Mesh Generation. Intl. J. Numer. Methods Eng. 41, 915–934.]]Google ScholarCross Ref
4. BOROUCHAKI, H. 1998. Geometric Surface Mesh. In Int. Conf. on Integrated and Manufacturing in Mechanical Engineering, 343–350.]]Google Scholar
5. BOSSEN, F., AND HECKBERT, P. 1996. A Pliant Method for Anisotropic Mesh Generation. In 5th Intl. Meshing Roundtable, 63–76.]]Google Scholar
6. BOTSCH, M., AND KOBBELT, L. 2001. Resampling Feature and Blend Regions in Polygonal Meshes for Surface Anti-Aliasing. In Eurographics proceedings, 402–410.]]Google Scholar
7. BRADY, M., PONCE, J., YUILLE, A., AND ASADA, H. 1985. Describing Surfaces. Journal of Computer Vision, Graphics, and Image Processing 32, 1–28.]]Google ScholarCross Ref
8. COHEN-STEINER, D., AND MORVAN, J.-M. 2003. Restricted delaunay triangulations and normal cycle. In Proc. 19th Annu. ACM Sympos. Comput. Geom.]] Google Scholar
9. D’AZEVEDO, E. F. 2000. Are Bilinear Quadrilaterals Better Than Linear Triangles? SIAM Journal on Scientific Computing 22(1), 198–217.]] Google ScholarDigital Library
10. DELMARCELLE, T., AND HESSELINK, L. 1994. The Topology of Symmetric, Second-Order Tensor Fields. In IEEE Visualization Proceedings, 140–145.]] Google Scholar
11. DESBRUN, M., MEYER, M., AND ALLIEZ, P. 2002. Intrinsic Parameterizations of Surface Meshes. In Proceedings of Eurographics, 209–218.]]Google Scholar
12. ECK, M., DEROSE, T., DUCHAMP, T., HOPPE, H., LOUNSBERY, M., AND STUETZLE, W. 1995. Multiresolution Analysis of Arbitrary Meshes. In ACM SIGGRAPH Conference Proceedings, 173–182.]] Google Scholar
13. FABRI, A., GIEZEMAN, G.-J., KETTNER, L., SCHIRRA, S., AND SCHÖNHERR, S. 2000. On the Design of CGAL, a Computational Geometry Algorithms Library. Softw. – Pract. Exp. 30, 11, 1167–1202. www.cgal.org.]] Google ScholarDigital Library
14. GARLAND, M., AND HECKBERT, P. 1998. Simplifying Surfaces with Color and Texture using Quadric Error Metrics. In IEEE Visualization Conf. Proc., 263–269.]] Google Scholar
15. GIRSHICK, A., INTERRANTE, V., HAKER, S., AND LEMOINE, T. 2000. Line Direction Matters: an Argument for the use of Principal Directions in 3D Line Drawings. In International Symposium on Non Photorealistic Animation and Rendering.]] Google ScholarDigital Library
16. GRAY, A., Ed. 1998. Modern Differential Geometry of Curves and Surfaces. Second edition. CRC Press.]] Google Scholar
17. GREENE, D. H. 1983. The Decomposition of Polygons into Convex Parts. In Computational Geometry, F. P. Preparata, Ed., vol. 1 of Adv. Comput. Res. JAI Press, Greenwich, Conn., 235–259.]]Google Scholar
18. GU, X., GORTLER, S., AND HOPPE, H. 2002. Geometry Images. In ACM SIGGRAPH Conference Proceedings, 355–361.]] Google Scholar
19. GUSKOV, I. 2002. An Anisotropic Mesh Parameterization Scheme. In Proceedings of 11th International Meshing Roundtable, 325–332.]]Google Scholar
20. HECKBERT, P., AND GARLAND, M. 1999. Optimal Triangulation and Quadric-Based Surface Simplification. Journal of Computational Geometry: Theory and Applications 14(1–3) (nov), 49–65.]] Google Scholar
21. HERTZMANN, A., AND ZORIN, D. 2000. Illustrating Smooth Surfaces. In ACM SIGGRAPH Conference Proceedings, 517–526.]] Google Scholar
22. HOPPE, H., DEROSE, T., DUCHAMP, T., MCDONALD, J., AND STUETZLE, W. 1993. Mesh Optimization. In ACM SIGGRAPH Conference Proceedings, 19–26.]] Google Scholar
23. HOPPE, H. 1996. Progressive Meshes. In ACM SIGGRAPH Conference Proceedings, 99–108.]] Google Scholar
24. INTERRANTE, V., FUCHS, H., AND PIZER, S. 1996. Illustrating Transparent Surfaces with Curvature-directed Strokes. In IEEE Visualization.]] Google Scholar
25. INTERRANTE, V. 1997. Illustrating Surface Shape in Volume Data via Principal Direction-Driven 3D Line Integral Convolution. In ACM SIGGRAPH Conference Proceedings, 109–116.]] Google Scholar
26. JOBARD, B., AND LEFER, W. 1997. Creating Evenly-Spaced Streamlines of Arbitrary Density. In Proceedings of the Eurographics Workshop on Visualization in Scientific Computing, 45–55.]]Google Scholar
27. KOBBELT, L., VORSATZ, J., LABSIK, U., AND SEIDEL, H.-P. 1999. A Shrink Wrapping Approach to Remeshing Polygonal Surfaces. Computer Graphics Forum, Eurographics ’99 issue 18, 119–130.]]Google Scholar
28. LEE, A. W. F., SWELDENS, W., SCHRÖDER, P., COWSAR, L., AND DOBKIN, D. 1998. MAPS: Multiresolution Adaptive Parameterization of Surfaces. In ACM SIGGRAPH Conference Proceedings, 95–104.]] Google Scholar
29. LEVIN, A. 2003. Polynomial generation and quasi-interpolation in stationary nonuniform subdivision. Computer Aided Geometric Design 20(1), 41–60.]] Google ScholarDigital Library
30. LÉVY, B., PETITJEAN, S., RAY, N., AND MAILLOT, J. 2002. Least Squares Conformal Maps for Automatic Texture Atlas Generation. In ACM SIGGRAPH Conference Proceedings, 362–371.]] Google Scholar
31. MEYER, M., DESBRUN, M., SCHRÖDER, P., AND BARR, A. H., 2002. Discrete Differential-Geometry Operators for Triangulated 2-Manifolds. Proceedings of VisMath.]]Google Scholar
32. PRESS, W., FLANNERY, B., TEUKOLSKY, S., AND VETTERLING, W. 1994. Numerical recipes in C — The art of scientific programming, 2nd ed. Cambridge University Press, UK.]] Google Scholar
33. ROSSL, C., AND KOBBELT, L. 2000. Line-art Rendering of 3D Models. In Proceedings of Pacific Graphics.]] Google ScholarCross Ref
34. SANDER, P., GORTLER, S., SNYDER, J., AND HOPPE, H. 2002. Signal-specialized parametrization. In Eurographics Workshop on Rendering 2002.]] Google ScholarDigital Library
35. SHIMADA, K., AND LIAO, J. 1998. Quadrilateral Meshing with Directionality Control through the Packing of Square Cells. In 7th Intl. Meshing Roundtable, 61–76.]]Google Scholar
36. SHIMADA, K. 1996. Anisotropic Triangular Meshing of Parametric Surfaces via Close Packing of Ellipsoidal Bubbles. In 6th Intl. Meshing Roundtable, 63–74.]]Google Scholar
37. SIMPSON, R. B. 1994. Anisotropic Mesh Transformations and Optimal Error Control. Appl. Num. Math. 14(1–3), 183–198.]] Google Scholar
38. STAM, J., AND LOOP, C., 2002. Quad/triangle subdivision. Preprint.]]Google Scholar
39. TAUBIN, G. 1995. Estimating the Tensor of Curvature of a Surface from a Polyhedral Approximation. In Proceedings of Fifth International Conference on Computer Vision, 902–907.]] Google Scholar
40. TRICOCHE, X. 2002. Vector and Tensor Field Topology Simplification, Tracking, and Visualization. PhD thesis, Universität Kaiserslautern.]]Google Scholar
41. TURK, G., AND BANKS, D. 1996. Image-Guided Streamline Placement. In ACM SIGGRAPH Conference Proceedings, 453–460.]] Google Scholar
42. TURK, G. 1992. Re-Tiling Polygonal Surfaces. In ACM SIGGRAPH Conference Proceedings, 55–64.]] Google Scholar
43. VERMA, V., KAO, D. T., AND PANG, A. 2000. A Flow-guided Streamline Seeding Strategy. In IEEE Visualization, 163–170.]] Google Scholar