“All-hex meshing using closed-form induced polycube”
Conference:
Type(s):
Title:
- All-hex meshing using closed-form induced polycube
Session/Category Title: MESHES
Presenter(s)/Author(s):
Moderator(s):
Abstract:
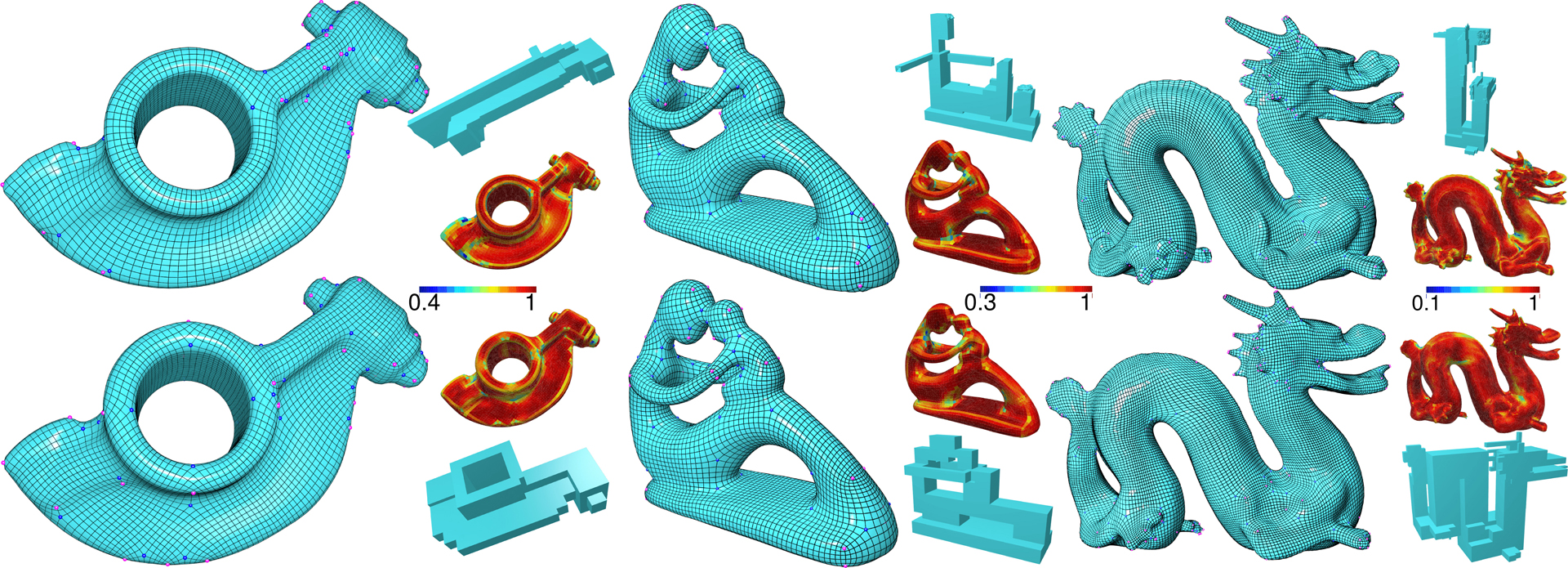
The polycube-based hexahedralization methods are robust to generate all-hex meshes without internal singularities. They avoid the difficulty to control the global singularity structure for a valid hexahedralization in frame-field based methods. To thoroughly utilize this advantage, we propose to use a frame field without internal singularities to guide the polycube construction. Theoretically, our method extends the vector fields associated with the polycube from exact forms to closed forms, which are curl free everywhere but may be not globally integrable. The closed forms give additional degrees of freedom to deal with the topological structure of high-genus models, and also provide better initial axis alignment for subsequent polycube generation. We demonstrate the advantages of our method on various models, ranging from genus-zero models to high-genus ones, and from single-boundary models to multiple-boundary ones.
References:
1. Aspert, N., Cruz, D. S., and Ebrahimi, T. 2002. MESH: measuring errors between surfaces using the hausdorff distance. In Proceedings of the 2002 IEEE International Conference on Multimedia and Expo, 705–708.Google Scholar
2. Bochkanov, S. n.d. Alglib (www.alglib.net).Google Scholar
3. Bommes, D., Zimmer, H., and Kobbelt, L. 2009. Mixed-integer quadrangulation. ACM Transactions on Graphics 28, 3 (July), 77:1–77:10. Google ScholarDigital Library
4. Carbonera, C., Shepherd, J., and Shepherd, J. 2006. A constructive approach to constrained hexahedral mesh generation. In Proceedings of the 15th International Meshing Roundtable. 435–452.Google Scholar
5. Dey, T. K., and Guha, S. 1998. Computing homology groups 3 of simplicial complexes in R3. J. ACM 45, 2 (Mar.), 266–287. Google ScholarDigital Library
6. Dey, T. K., Fan, F., and Wang, Y. 2013. An efficient computation of handle and tunnel loops via reeb graphs. ACM Transactions on Graphics 32, 4 (July), 32:1–32:10. Google ScholarDigital Library
7. Gao, X., Deng, Z., and Chen, G. 2015. Hexahedral mesh reparameterization from aligned base-complex. ACM Transactions on Graphics 34, 4 (July), 142:1–142:10. Google ScholarDigital Library
8. García, I., Xia, J., He, Y., Xin, S., and Patow, G. 2013. Interactive applications for sketch-based editable polycube map. IEEE Transactions on Visualization and Computer Graphics 19, 7, 1158–1171. Google ScholarDigital Library
9. Gregson, J., Sheffer, A., and Zhang, E. 2011. All-hex mesh generation via volumetric polycube deformation. Computer Graphics Forum 30, 5, 1407–1416.Google ScholarCross Ref
10. Huang, J., Tong, Y., Wei, H., and Bao, H. 2011. Boundary aligned smooth 3d cross-frame field. ACM Transactions on Graphics 30, 6 (Dec), 143:1–143:8. Google ScholarDigital Library
11. Huang, J., Jiang, T., Shi, Z., Tong, Y., Bao, H., and Desbrun, M. 2014. l1-based construction of polycube maps from complex shapes. ACM Transactions on Graphics 33, 3 (June), 25:1–25:11. Google ScholarDigital Library
12. Jiang, T., Huang, J., Wang, Y., Tong, Y., and Bao, H. 2014. Frame field singularity correction for automatic hexahedralization. IEEE Transactions on Visualization and Computer Graphics 20, 8, 1189–1199. Google ScholarDigital Library
13. Jiang, T., Fang, X., Huang, J., Bao, H., Tong, Y., and Desbrun, M. 2015. Frame field generation through metric customization. ACM Transactions on Graphics 34, 4 (July), 40:1–40:11. Google ScholarDigital Library
14. Kowalski, N., Ledoux, F., and Frey, P. 2014. Block-structured hexahedral meshes for cad models using 3d frame fields. Procedia Engineering 82, 59–71.Google ScholarCross Ref
15. Li, Y., Liu, Y., Xu, W., Wang, W., and Guo, B. 2012. All-hex meshing using singularity-restricted field. ACM Transactions on Graphics 31, 6 (Nov.), 177:1–177:11. Google ScholarDigital Library
16. Lin, J., Jin, X., Fan, Z., and Wang, C. C. L. 2008. Automatic polycube-maps. In Proceedings of the 5th International Conference on Advances in Geometric Modeling and Processing, 3–16. Google ScholarDigital Library
17. Livesu, M., Vining, N., Sheffer, A., Gregson, J., and Scateni, R. 2013. Polycut: Monotone graph-cuts for polycube base-complex construction. ACM Transactions on Graphics 32, 6 (Nov.), 171:1–171:12. Google ScholarDigital Library
18. Livesu, M., Sheffer, A., Vining, N., and Tarini, M. 2015. Practical hex-mesh optimization via edge-cone rectification. ACM Transactions on Graphics 34, 4 (July), 141:1–141:11. Google ScholarDigital Library
19. Nieser, M., Reitebuch, U., and Polthier, K. 2011. Cube-cover – parameterization of 3d volumes. Computer Graphics Forum 30, 5, 1397–1406.Google ScholarCross Ref
20. Panozzo, D., Puppo, E., Tarini, M., and Sorkine-Hornung, O. 2014. Frame fields: Anisotropic and nonorthogonal cross fields. ACM Transactions on Graphics 33, 4 (July), 134:1–134:11. Google ScholarDigital Library
21. Sheffer, A., Etzion, M., Rappoport, A., and Bercovier, M. 1999. Hexahedral mesh generation using the embedded voronoi graph. Engineering with Computers 15, 3, 248–262.Google ScholarCross Ref
22. Shepherd, J. F., and Johnson, C. R. 2008. Hexahedral mesh generation constraints. Engineering With Computers 24, 3, 195–213.Google ScholarDigital Library
23. Shepherd, J. F., Mitchell, S. A., Knupp, P. M., and White, D. R. 2000. Methods for multisweep automation. In Proceedings of the 9th International Meshing Roundtable, 77–87.Google Scholar
24. Shimada, K. 2006. Current trends and issues in automatic mesh generation. Computer-Aided Design & Applications 3, 741–750.Google ScholarCross Ref
25. Staten, M., Owen, S., and Blacker, T. 2005. Unconstrained paving and plastering: A new idea for all hexahedral mesh generation. In Proceedings of the 14th International Meshing Roundtable. 399–416.Google Scholar
26. Tarini, M., Hormann, K., Cignoni, P., and Montani, C. 2004. Polycube-maps. ACM Transactions on Graphics 23, 3 (Aug.), 853–860. Google ScholarDigital Library
27. Wächter, A., and Biegler, T. L. 2005. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Mathematical Programming 106, 1, 25–57.Google ScholarCross Ref