“2-D shape blending: an intrinsic solution to the vertex path problem” by Sederberg, Gao, Wang and Mu
Conference:
Type(s):
Title:
- 2-D shape blending: an intrinsic solution to the vertex path problem
Presenter(s)/Author(s):
Abstract:
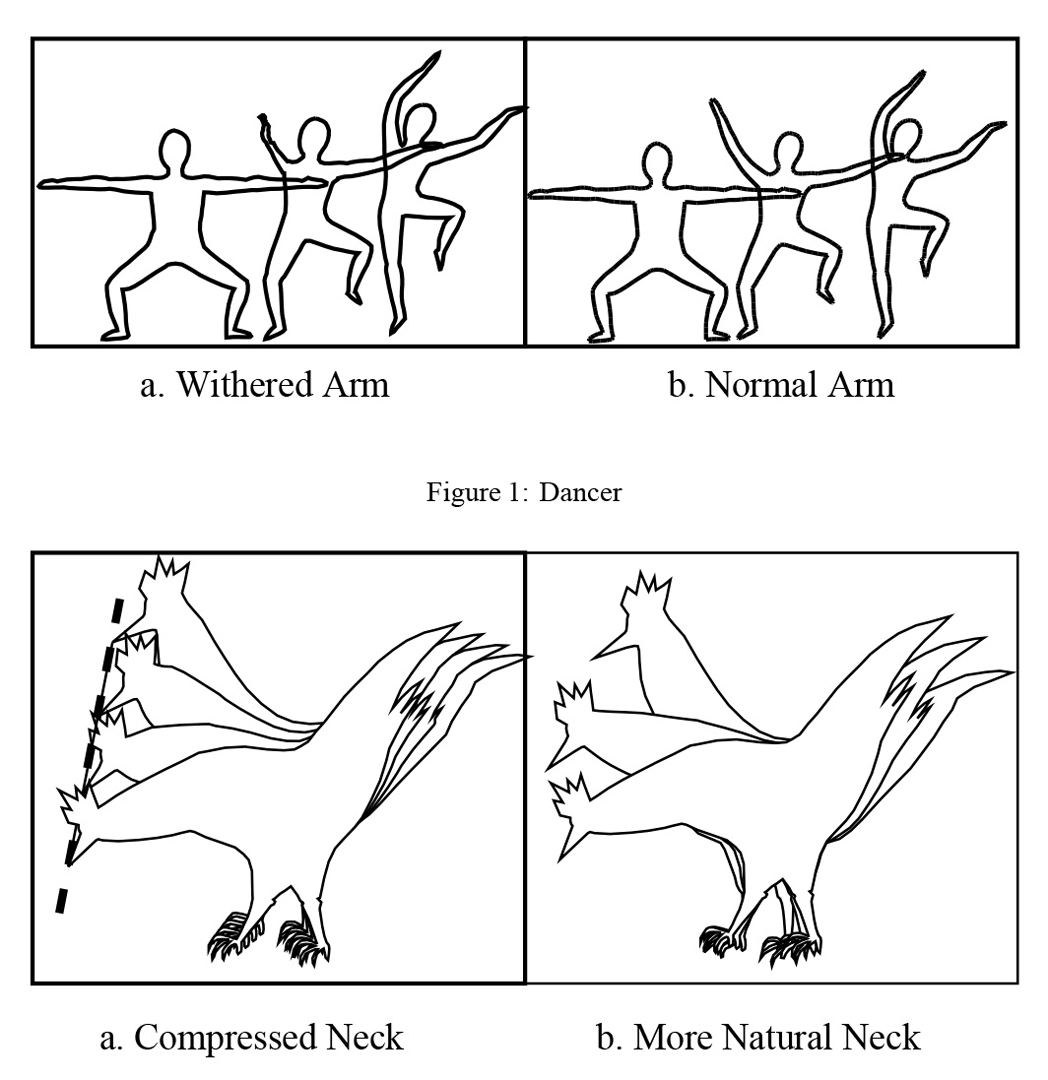
This paper presents an algorithmfor determiningthe paths along which
corresponding vertices travel in a 2–D shape blending. Rather than
considering the vertex paths explicitly, the algorithm defines the intermediate shapes by interpolating the intrinsic definitions of the initial
and final shapes. The algorithm produces shape blends which generally are more satisfactory than those produced using linear or cubic
curve paths. Particularly, the algorithm can avoid the shrinkage that
normally occurs when rotating rigid bodies are linearly blended, and
avoids kinks in the blend when there were none in the key polygons.
References:
1. J. Alan Adams. The intrinsic method for curve definition. Computer-Aided Design, 7(4):243-249,1975.
2. Harold J. Bailey, Kathleen M. Brautigam, and Trudy H. Doran. Apple Logo. Brady Communications Company, Inc., Bowie, MD, 1984.
3. Shenchang Eric Chen and Richard Parent. Shape averaging and its applications to industrial design. IEEE CG&A, 9(1):47-54,1989.
4. Peisheng Gao. 2-d shape blending: an intrinsic solution to the vertex path problem. Master’s thesis, Brigham Young University, Department of Civil Engineering, 1993.
5. Andrew Glassner. Metamorphosis. preprint, 1991.
6. John F. Hughes. Scheduled fourier volume morphing. Computer Graphics (P1vc. SIGGRAPH), 26(2):43-46,1992.
7. Anil Kaul and Jarek Rossignac. Solid-interpolating deformations: Construction and animation of PIPs. In F.H. Post and W. Barth, editors, P~vc. Eurographics ’91, pages 4931505. Elsevier Science Publishers B.V, 1991.
8. James R. Kent, Wayne E. Carlson, and Richard E. Parent. Shape transformation for polyhedral objects. Computer Graphics (P1vc. SIGGRAPH), 26(2):47-54, 1992.
9. S. C. Malik. MathematicaIAnalysis. John Wiley & Sons, Inc., New York, 1984.
10. Eadweard Muybridge. Animals in Motion. Dover Publications, Inc., New York, 1957.
11. Thomas W. Sederberg and Eugene Greenwood. Shape blending of 2-d piecewise curves. Submitted.
12. Thomas W. Sederberg and Eugene Greenwood. A physically based approach to 2-d shape blending. Computer Graphics (P1vc. SIGGRAPH), 26(2):25-34, 1992.
13. Yoshihisa Shinagawa and Tosiyasu L. Kunii. The differential model: A model for animating transformation of objects using differntial information. In Tosiyasu L. Kunii, editor, Modeling in Computer Graphics, pages 5-15, Tokyo, 1991. Springer-Verlag.
14. Geoffrey Slinker. Inbetweening using a physically based model and nonlinear path interpolation. Master’s thesis, Brigham Young University, Department of Computer Science, 1992.