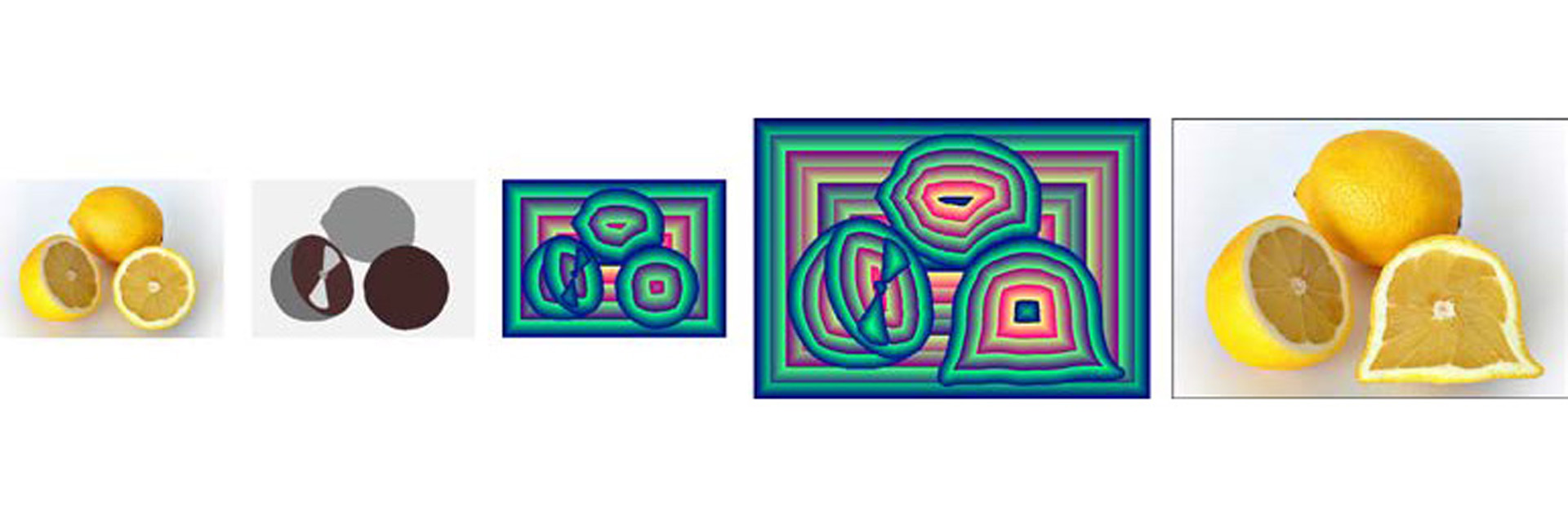
“Yet Another Vector Representation for Images Using Eikonal Surfaces” by Zieliński, Tsai and Ouhyoung
Conference:
Type(s):
Entry Number: 110
Title:
- Yet Another Vector Representation for Images Using Eikonal Surfaces
Presenter(s)/Author(s):
Abstract:
Scaling and deformation of raster images almost always causes the decrease of image quality. On the other hand vector graphics offers easy image manipulation without any quality loss. Many algorithms have been presented in the recent years to convert raster images into vector ones. However, all the solutions assume that the image discontinuities need to be decomposed into a set of multiple piecewise smooth surfaces. This may cause data losses or extremely high complexity of the underlying vector structure, in the areas with high variance (noise, patterns etc.). Our method does not rely on gradients generated from a triangular decomposition of the image plane and piecewise smooth loop subdivision surfaces [Liao et al. 2012], nor extracted diffusion curves defining the gradient propagation [Orzan et al. 2008]. Instead it uses separately sampled pixel values. It gives a user the freedom to manipulate easily the elements of the raster image as it is in case of vector graphics. At the same time it keeps the underlying image representation simple, even in the areas of high variance. Sharpness of details is achieved by proper segmentation and edge selection. In the worst case the quality gets reduced to the correspondent interpolated raster quality.
References:
- Liao, Z., Hoppe, H., Forsyth, D., and Yu, Y. 2012. A subdivision-based representation for vector image editing. IEEE Transactions on Visualization and Computer Graphics 18, 1858–1867.
- Orzan, A., Bousseau, A., Winnemöller, H., Barla, P., Thollot, J., and Salesin, D. 2008. Diffusion curves: A vector representation for smooth-shaded images. In ACM Transactions on Graphics (Proceedings of ACM SIGGRAPH 2008), ACM, SIGGRAPH ’08, 92:1–92:8.
Acknowledgements:
This work is partially funded by NSC 101-2221-E-002-204-MY2 and 102-2622-E-002-013-CC2 (Taiwan).