“Voxel cores: efficient, robust, and provably good approximation of 3D medial axes” by Yan, Letscher and Ju
Conference:
Type(s):
Entry Number: 44
Title:
- Voxel cores: efficient, robust, and provably good approximation of 3D medial axes
Session/Category Title: An Immersion in Computational Geometry
Presenter(s)/Author(s):
Moderator(s):
Abstract:
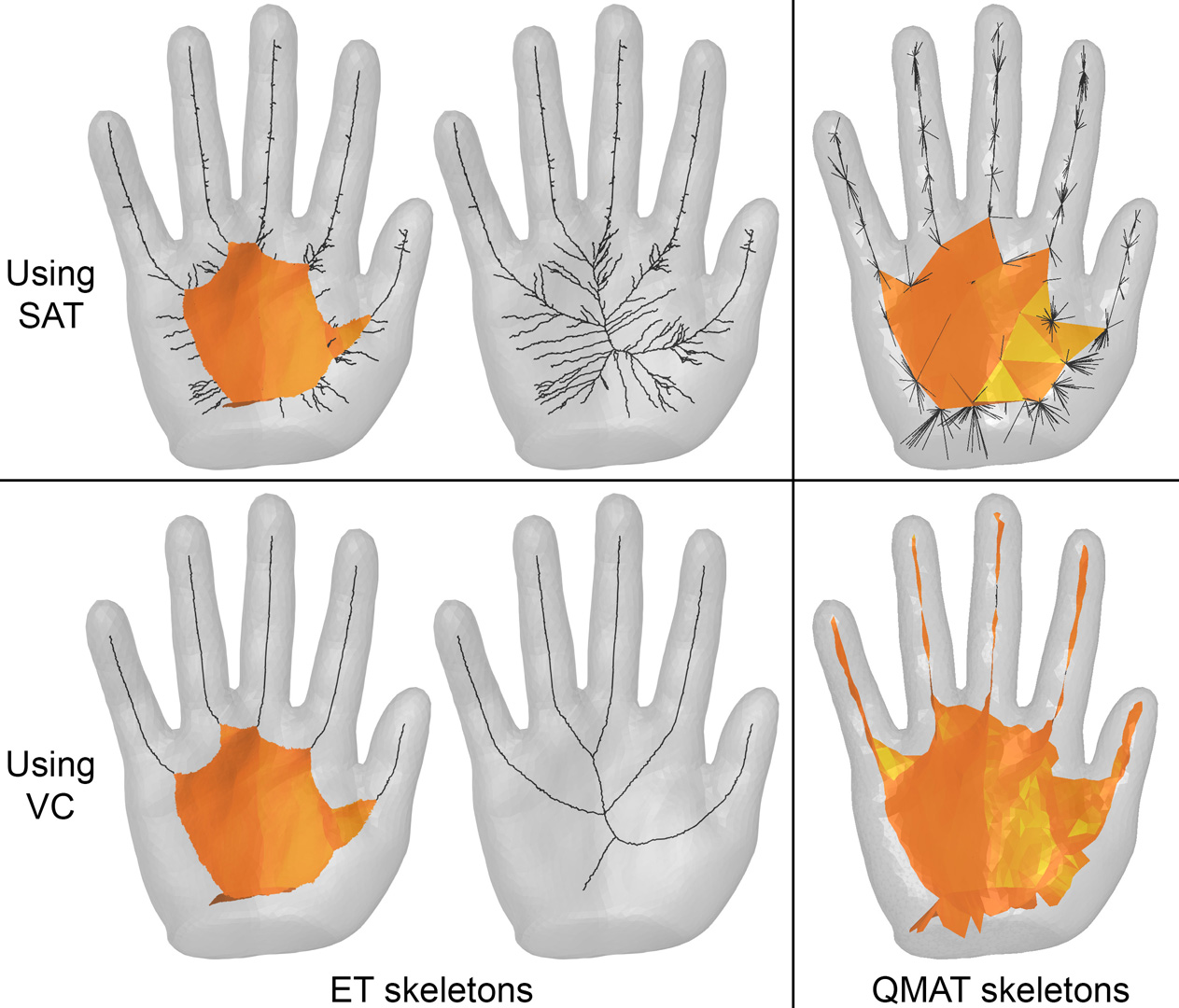
We present a novel algorithm for computing the medial axes of 3D shapes. We make the observation that the medial axis of a voxel shape can be simply yet faithfully approximated by the interior Voronoi diagram of the boundary vertices, which we call the voxel core. We further show that voxel cores can approximate the medial axes of any smooth shape with homotopy equivalence and geometric convergence. These insights motivate an algorithm that is simple, efficient, numerically stable, and equipped with theoretical guarantees. Compared with existing voxel-based methods, our method inherits their simplicity but is more scalable and can process significantly larger inputs. Compared with sampling-based methods that offer similar theoretical guarantees, our method produces visually comparable results but more robustly captures the topology of the input shape.
References:
1. Nina Amenta, Sunghee Choi, and Ravi Krishna Kolluri. 2001. The power crust, unions of balls, and the medial axis transform. Computational Geometry 19, 2-3 (2001), 127–153. Google ScholarDigital Library
2. Nina Amenta and Ravi Krishna Kolluri. 2001. The medial axis of a union of balls. Comput. Geom. 20, 1-2 (2001), 25–37. Google ScholarDigital Library
3. Carlo Arcelli and Gabriella Sanniti di Baja. 1993. Euclidean skeleton via centre-of-maximal-disc extraction. Image and Vision Computing 11, 3 (1993), 163–173.Google ScholarCross Ref
4. Carlo Arcelli, Gabriella Sanniti di Baja, and Luca Serino. 2011. Distance-driven skeletonization in voxel images. IEEE Transactions on Pattern Analysis and Machine Intelligence 33, 4 (2011), 709–720. Google ScholarDigital Library
5. Dominique Attali and Jean-Daniel Boissonnat. 2004. A linear bound on the complexity of the Delaunay triangulation of points on polyhedral surfaces. Discrete & Computational Geometry 31, 3 (2004), 369–384. Google ScholarDigital Library
6. Dominique Attali and Annick Montanvert. 1996. Modeling noise for a better simplification of skeletons. In Proceedings 1996 International Conference on Image Processing, Lausanne, Switzerland, September 16-19, 1996. 13–16.Google ScholarCross Ref
7. Gilles Bertrand and Grégoire Malandain. 1994. A new characterization of three-dimensional simple points. Pattern Recognition Letters 15, 2 (1994), 169–175. Google ScholarDigital Library
8. Anders Björner, Bernhard Korte, and László Lovász. 1985. Homotopy properties of greedoids. Advances in Applied Mathematics 6, 4 (1985), 447–494. Google ScholarDigital Library
9. H. Blum. 1967. A transformation for extracting new descriptors of form. Models for the Perception of Speech and Visual Form (1967), 362–80.Google Scholar
10. J. Brandt and V. Algazi. 1992. Continuous skeleton computation by Voronoi diagram. CVGIP: Image Understanding 55, 3 (1992), 329 — 338. Google ScholarDigital Library
11. Frederic Cazals, Aditya Parameswaran, and Sylvain Pion. 2008. Robust construction of the three-dimensional flow complex. In Proceedings of the twenty-fourth annual symposium on Computational geometry. ACM, 182–191. Google ScholarDigital Library
12. Frédéric Chazal and André Lieutier. 2005. The “λ-medial axis”. Graphical Models 67, 4 (2005), 304–331. Google ScholarDigital Library
13. Frédéric Chazal and André Lieutier. 2008. Smooth manifold reconstruction from noisy and non-uniform approximation with guarantees. Computational Geometry 40, 2 (2008), 156–170. Google ScholarDigital Library
14. Tim Culver, John Keyser, and Dinesh Manocha. 2004. Exact computation of the medial axis of a polyhedron. Computer Aided Geometric Design 21, 1 (2004), 65–98. Google ScholarDigital Library
15. Tamal K. Dey and Wulue Zhao. 2003. Approximating the Medial Axis from the Voronoi Diagram with a Convergence Guarantee. Algorithmica 38, 1 (2003), 179–200. Google ScholarDigital Library
16. Michal Etzion and Ari Rappoport. 2002. Computing Voronoi skeletons of a 3-D polyhedron by space subdivision. Computational Geometry 21, 3 (2002), 87–120. Google ScholarDigital Library
17. Mark Foskey, Ming C Lin, and Dinesh Manocha. 2003. Efficient computation of a simplified medial axis. In Proceedings of the eighth ACM symposium on Solid modeling and applications. ACM, 96–107. Google ScholarDigital Library
18. Yaorong Ge and J Michael Fitzpatrick. 1996. On the generation of skeletons from discrete Euclidean distance maps. IEEE Transactions on Pattern Analysis and Machine Intelligence 18, 11 (1996), 1055–1066. Google ScholarDigital Library
19. Joachim Giesen, Edgar A Ramos, and Bardia Sadri. 2006. Medial axis approximation and unstable flow complex. In Proceedings of the twenty-second annual symposium on Computational geometry. ACM, 327–336. Google ScholarDigital Library
20. Wim H Hesselink and Jos BTM Roerdink. 2008. Euclidean skeletons of digital image and volume data in linear time by the integer medial axis transform. IEEE Transactions on Pattern Analysis and Machine Intelligence 30, 12 (2008), 2204–2217. Google ScholarDigital Library
21. Christoph M Hoffmann. 1990. How to construct the skeleton of CSG objects. (1990).Google Scholar
22. Andrei C Jalba, Jacek Kustra, and Alexandru C Telea. 2013. Surface and curve skeletonization of large 3D models on the GPU. IEEE transactions on pattern analysis and machine intelligence 35, 6 (2013), 1495–1508. Google ScholarDigital Library
23. Andrei C Jalba, Andre Sobiecki, and Alexandru C Telea. 2016. An unified multiscale framework for planar, surface, and curve skeletonization. IEEE transactions on pattern analysis and machine intelligence 38, 1 (2016), 30–45. Google ScholarDigital Library
24. Tao Ju. 2004. Robust repair of polygonal models. ACM Transactions on Graphics (TOG) 23, 3 (2004), 888–895. Google ScholarDigital Library
25. Reinhard Klette and Azriel Rosenfeld. 2004. Digital geometry: Geometric methods for digital picture analysis. Elsevier. Google ScholarDigital Library
26. Jacques-Olivier Lachaud and Boris Thibert. 2016. Properties of gauss digitized shapes and digital surface integration. Journal of Mathematical Imaging and Vision 54, 2 (2016), 162–180. Google ScholarDigital Library
27. Yong-Gu Lee and Kunwoo Lee. 1997. Computing the medial surface of a 3-D boundary representation model. Advances in Engineering Software 28, 9 (1997), 593–605. Google ScholarDigital Library
28. Pan Li, Bin Wang, Feng Sun, Xiaohu Guo, Caiming Zhang, and Wenping Wang. 2015. Q-MAT: Computing Medial Axis Transform By Quadratic Error Minimization. ACM Trans. Graph. 35, 1 (Dec. 2015), 8:1–8:16. Google ScholarDigital Library
29. André Lieutier. 2003. Any Open Bounded Subset of Rn Has the Same Homotopy Type Than Its Medial Axis. In Proceedings of the Eighth ACM Symposium on Solid Modeling and Applications (SM ’03). 65–75. Google ScholarDigital Library
30. L. Liu, Erin W. Chambers, David Letscher, and T. Ju. 2010. A simple and robust thinning algorithm on cell complexes. Comput. Graph. Forum 29, 7 (2010), 2253–2260.Google ScholarCross Ref
31. Jaehwan Ma, Sang Won Bae, and Sunghee Choi. 2012. 3D medial axis point approximation using nearest neighbors and the normal field. The Visual Computer 28, 1 (2012), 7–19. Google ScholarDigital Library
32. Balint Miklos, Joachim Giesen, and Mark Pauly. 2010. Discrete Scale Axis Representations for 3D Geometry. ACM Trans. Graph. 29, 4 (July 2010), 101:1–101:10. Google ScholarDigital Library
33. Victor Milenkovic. 1993. Robust Construction of the Voronoi Diagram of a Polyhedron.. In CCCG, Vol. 93. 473–478.Google Scholar
34. Suraj Musuvathy, Elaine Cohen, and James Damon. 2011. Computing medial axes of generic 3D regions bounded by B-spline surfaces. Computer-Aided Design 43, 11 (2011), 1485–1495. Google ScholarDigital Library
35. Kálmán Palágyi and Attila Kuba. 1999. A parallel 3D 12-subiteration thinning algorithm. Graphical Models and Image Processing 61, 4 (1999), 199–221. Google ScholarDigital Library
36. Chris Pudney. 1998. Distance-ordered homotopic thinning: a skeletonization algorithm for 3D digital images. Computer Vision and Image Understanding 72, 3 (1998), 404–413. Google ScholarDigital Library
37. M Ramanathan and B Gurumoorthy. 2010. Interior Medial Axis Transform computation of 3D objects bound by free-form surfaces. Computer-Aided Design 42, 12 (2010), 1217–1231. Google ScholarDigital Library
38. Dennie Reniers, Jarke van Wijk, and Alexandru Telea. 2008. Computing Multiscale Curve and Surface Skeletons of Genus 0 Shapes Using a Global Importance Measure. IEEE Transactions on Visualization and Computer Graphics 14, 2 (2008), 355–368. Google ScholarDigital Library
39. Martin Rumpf and Alexandru Telea. 2002. A continuous skeletonization method based on level sets. In Proceedings of the symposium on Data Visualisation 2002. Eurographics Association, 151–ff. Google ScholarDigital Library
40. Punam K Saha, Gunilla Borgefors, and Gabriella Sanniti di Baja. 2016. A survey on skeletonization algorithms and their applications. Pattern Recognition Letters 76 (2016), 3–12. Google ScholarDigital Library
41. Punam K. Saha and Bidyut Baran Chaudhuri. 1994. Detection of 3-D simple points for topology preserving transformations with application to thinning. IEEE transactions on pattern analysis and machine intelligence 16, 10 (1994), 1028–1032. Google ScholarDigital Library
42. Evan C. Sherbrooke, Nicholas M. Patrikalakis, and Erik Brisson. 1996. An Algorithm for the Medial Axis Transform of 3D Polyhedral Solids. IEEE Transactions on Visualization and Computer Graphics 2, 1 (1996), 44–61. Google ScholarDigital Library
43. Hang Si. 2015. TetGen, a Delaunay-based quality tetrahedral mesh generator. ACM Transactions on Mathematical Software (TOMS) 41, 2 (2015), 11. Google ScholarDigital Library
44. Kaleem Siddiqi, Sylvain Bouix, Allen Tannenbaum, and Steven W. Zucker. 2002. Hamilton-Jacobi Skeletons. International Journal of Computer Vision 48, 3 (July 2002), 215–231. Google ScholarDigital Library
45. Kaleem Siddiqi and Stephen M. Pizer. 2008. Medial Representations. Springer.Google Scholar
46. André Sobiecki, Andrei Jalba, and Alexandru Telea. 2014. Comparison of curve and surface skeletonization methods for voxel shapes. Pattern Recognition Letters 47 (2014), 147–156. Google ScholarDigital Library
47. Peer Stelldinger, Longin Jan Latecki, and Marcelo Siqueira. 2007. Topological equivalence between a 3D object and the reconstruction of its digital image. IEEE transactions on pattern analysis and machine intelligence 29, 1 (2007). Google ScholarDigital Library
48. Svetlana Stolpner and Kaleem Siddiqi. 2006. Revealing significant medial structure in polyhedral meshes. In 3D Data Processing, Visualization, and Transmission, Third International Symposium on. IEEE, 365–372. Google ScholarDigital Library
49. Avneesh Sud, Liangjun Zhang, and Dinesh Manocha. 2006. Homotopy Preserving Approximate Voronoi Diagram of 3D Polyhedron. Technical Report. Technical report.Google Scholar
50. Andrea Tagliasacchi, T. Delame, M. Spagnuolo, N. Amenta, and A. Telea. 2016. 3D Skeletons: A State-of-the-Art Report. In Eurographics. Google ScholarDigital Library
51. Roger C. Tam and Wolfgang Heidrich. 2003. Shape Simplification Based on the Medial Axis Transform. In 14th IEEE Visualization 2003 Conference (VIS 2003), 19-24 October 2003, Seattle, WA, USA. 481–488. Google ScholarDigital Library
52. YF Tsao and King Sun Fu. 1981. A parallel thinning algorithm for 3-D pictures. Computer graphics and image processing 17, 4 (1981), 315–331.Google Scholar
53. Yajie Yan, Kyle Sykes, Erin Chambers, David Letscher, and Tao Ju. 2016. Erosion thickness on medial axes of 3D shapes. ACM Transactions on Graphics (TOG) 35, 4 (2016), 38. Google ScholarDigital Library