“Volumetric shape description of range data using “Blobby Model”” by Muraki

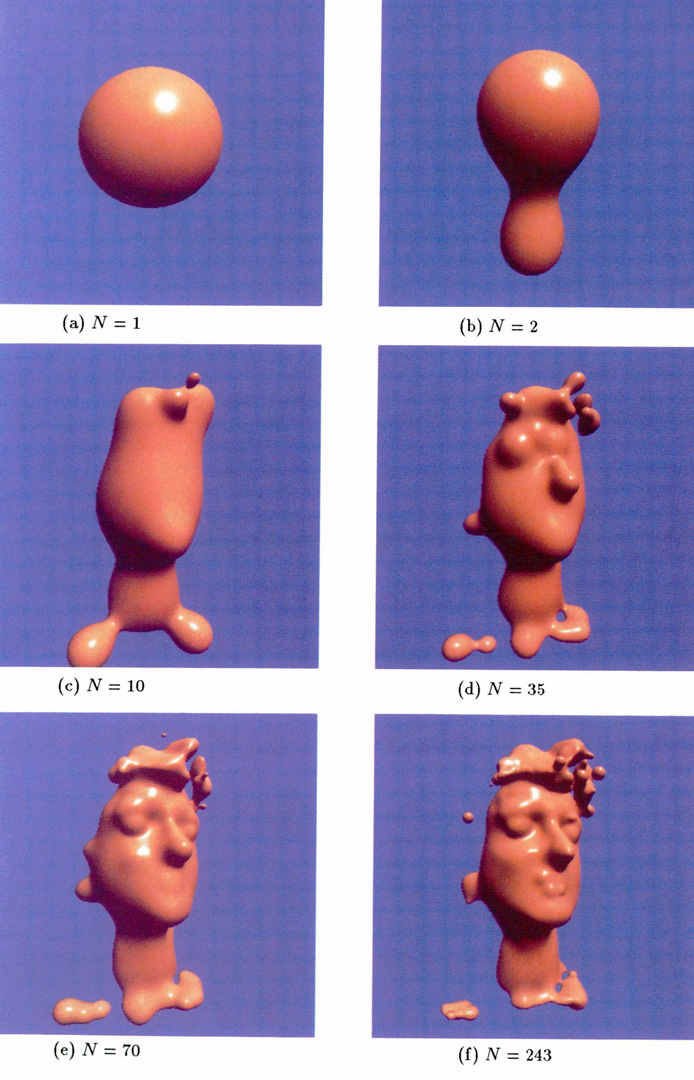
Recently in the field of computer vision, there have been many attempts to obtain a symbolic shape description of an object by fitting simple primitives to the range data of the object. In this paper, we introduce the “Blobby Model” for automatically generating a shape description from range data. This model can express a 3D surface as an isosurface of a scalar field which is produced by a number of field generating primitives. The fields from many primitives are blended with each other and can form a very complicated shape. To determine the number and distribution of primitives required to adequately represent a complex 3D surface, an energy function is minimized which measures the shape difference between the range data and the “Blobby Model”. We start with a single primitive and introduce more primitives by splitting each primitive into two further primitives so as to reduce the energy value. In this manner, the shape of the 3D object is slowly recovered as the isosurface produced by many primitives. We have successfully applied this method to human face range data and typical results are shown. The method herein does not require any prior range segmentation.

1. Marr, D.: “Vision”, Freeman, San Francisco, 1982.
2. Barr, A.H.: “S up erquadrics and Angle-Preserving Transformations”, IEEE Computer Graphics and Applications, Vol.1, No.l, pp.ll-23, 1981.
3. Kaneta, M., Yokoya, N. and Yamamoto, K.: “Recovery of Superquadric Primitives from Range images by Simulated Annealing”,SIG Notes of the Information Processing Society o} Japan, SIGCV 65-6, 1990. (in Japanese).
4. Pentland, A.P.: “Recognition by Parts”, SRI International Technical Note, No.406, 1986.
5. Boult, T.E. and Gross, A.D.: “Recovery of Superquadrics from Depth Information”, Proc. of Workshop on Spatial Reasoning and Multi.Sensor Fusion, pp.128-137, 1987.
6. Horikosi, T. and Kasahara, H.: “A 3D Indexing Method for an Image Database”, Technical Report of the Institute of Electronics, ln}ormation and Communication Engineers of Japan, IE88-111, pp. 33-40, 1988. (in Japanese).
7. Solina, F. and Bajcsy, R.’ “Recovery of Parametric Models from Range Images: The Case for Superquadrics with Global Deformations”, IEEE Trans. PAMI, Vol. 12, No.2, pp.131-147, 1990.
8. Ferrie, F.P., Lagarde,J. and Whaite, P.: “Recovery of Volumetric Object Descriptions From Laser Rangefinder Images”, Proc. of ECCV 90, pp.387- 396, 1990.
9. Blinn, J.F.: “A Generalization of Algebraic Surface Drawing”, A CM Trans. on Graphics, Vol.1, No.3, pp.235-256, 1982.
10. Nishimura, H., Hirai, M., Kawai, T., Kawata, T., Shirakawa, I. and Omura, K.”Object Modeling by Distribution Function and a Method of Image Generation”, Trans. IEICE Japan, VoI.J68-D, No.4, pp.718-725, 1985. (in Japanese).
11. Wyvill, G., McPheeters, C. and Wyvill, B.:”Data Structure for Soft Objects”, The Visual Computer, Vol.2, pp.227-234, 1986.
12. Rioux, M. and Cournoyer, L.: “The NRCC Threedimensional Image Data Files”, Thec. Report, CNR C 29077, National Research Council Canada, Ottawa, Canada, 1988.
13. Press, W.H., Flannery, B.P., Teukolsky, S.A. and Vetterling, W.T.: “Numerical Recipes in C”, Cambridge, 1988.
14. Kalra, D. and Barr, A.H.: “Guaranteed Ray Intersections with Implicit Surfaces”, Computer Graphics (SIGGRA PH ’89 Proceedings), Vol.23, No.3, pp. 297-306, 1989.