“Visibility preprocessing for interactive walkthroughs” by Teller and Séquin

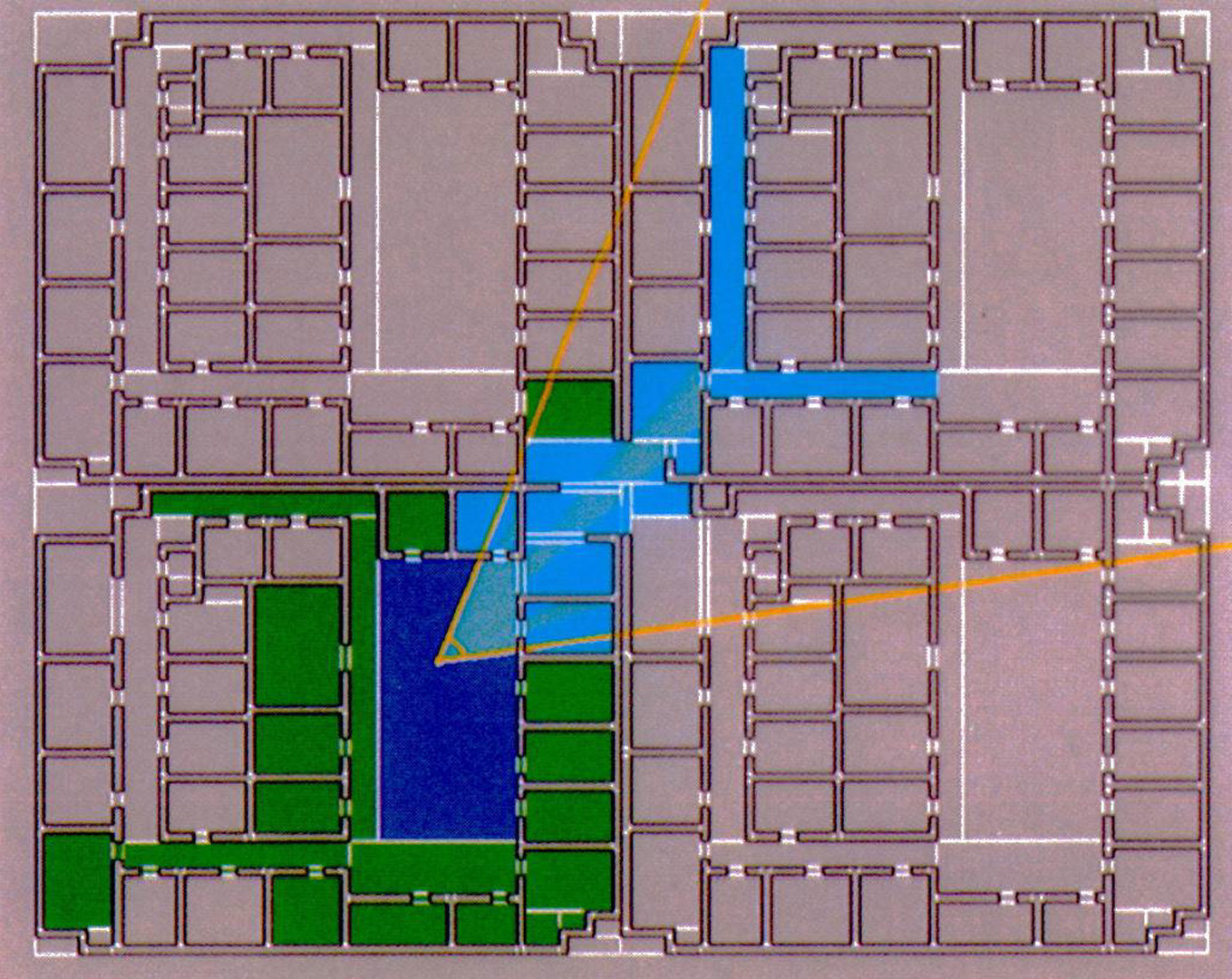
The number of polygons comprising interesting architectural models is many more than can be rendered at interactive frame rates. However, due to occlusion by opaque surfaces (e.g., walls), only a small fraction of a typical model is visible from most viewpoints.We describe a method of visibility preprocessing that is efficient and effective for axis-aligned or axial architectural models. A model is subdivided into rectangular cells whose boundaries coincide with major opaque surfaces. Non-opaque portals are identified on cell boundaries, and used to form an adjacency graph connecting the cells of the subdivision. Next, the cell-to-cell visibility is computed for each cell of the subdivision, by linking pairs of cells between which unobstructed sightlines exist.During an interactive walkthrough phase, an observer with a known position and view cone moves through the model. At each frame, the cell containing the observer is identified, and the contents of potentially visible cells are retrieved from storage. The set of potentially visible cells is further reduced by culling it against the observer’s view cone, producing the eye-to-cell visibility. The contents of the remaining visible cells are then sent to a graphics pipeline for hidden-surface removal and rendering.Tests on moderately complex 2-D and 3-D axial models reveal substantially reduced rendering loads.

1. John M. Airey. Ire’teasing Update Rates in the Building Walkthrough System ~’ith Automatic ModeI-Sl~a~’e Subdivision and Potentially Visible Set Cah’ulations. PhD thesis, UNC Chapel Hill, 1990,
2. John M. Airey, John H. Rohlf, and Frederick P. Brooks Jr. Towards image realism with interactive update rates in complex virtual building environments. ACM SIGGRAPH Special Issue on 1990 Symposium on Interacti~’e 3D Graphics, 24(2):41-50, 1990.
3. Kurl Akeley. The Silicon Graphics 4D/240GTX superworkstation. IEEE Computer Graphi~’s and Appli~’ations, 9(4 ):239- 246, 1989,
4. J.L. Bentley. Multidimensional binary search trees used for associative searching. Communications qfthe ACM, 18:509- 517, 1975.
5. B. Chazelle and L.J. Guibas. Visibility and intersection problems in plane geometry, In Pro~’. !’~ ACM Symposium on Comtmtational Geometry, pages 135-1,46, 1985.
6. Frank C. Crow. Shadow algorithms for computer graphics. Conqmter Graphi~’s (Pro~’. SIGGRAPtt “77), 11(2):242-248, 1977.
7. David R Dobkin and Diane L. Souvaine. Detecting the intersection of convex objects in the plane. Technical Report No. 89-9, DIMACS, 1989.
8. H. Fuchs, Z. Kedem, and B. Naylor, On visible surface generalion by a priori tree structures. Computer Graphics (Pro~’. SIG- GRAPH ’80), 14(3):124-133, July 1980.
9. Akira Fujimolo and Kansei lwata. Accelerated ray tracing. In Computer Graphi~’s: Visual Te~’hnohJ.~y and Art (Pro~. Computer Graphi~’s Tokyo ‘,~~5 ), pages 41-65, 1985.
10. Benjamin Garlick, Daniel R. Baum, and James M. Winger, Interactive viewing of large geometric databases using multiprocessor graphics workstations. In SIGGRAPtt ’90 Cours(‘ Notes (Parallel Algorithms and Ar~’hite~tures }?~r 3D Image Generation ), August 1990.
11. Andrew S. Glassner. Space subdivision for fast ray tracing. IEEE Computer Graphi~.s ctttd Appli~’ations, 4( 10):15-22, October 1984.
12. John E. Hershberger. Effu’ient AIgorithrn.~ for Shortest Path and Visibility Problems. PhD thesis, Stanford University. June 1987.
13. Michael E. Hohmeyer and Seth J, Teller. Slabbing isothetic rectangles and boxes in O(~ Ig ~) time (in preparation).
14. David Kirk and Douglas Voorhies. The rendering architecture of the DNI(X)()OVS. Computer Graphi~s ~Ptw~’. SIGGRAPH ’90), 24(4):299-307, August 1990.
15. N. Megiddo. Linear-time algorithms for linear programming in R~ and related problems, SIAM Journal (_’rmtputing, 12:759- 776. 1983.
16. Joseph O’ Rourke. Art Gallery Theorems and Algorithms. Oxford University Press, 1987.
17. Michael S. Paterson and F. Frances Yao. Efficient binary space partitions for hidden-surface removal and solid modeling. Dis- ~rete and Computational Geometry, 5(5 ):485-503, 199(t.
18. W. H. Plantinga and C. R. Dyer. An algorithm for constructing the aspect graph, In Piw~’. IEEE Syrup. Foundations of Computer Scienc’e, pages 123-131, ! 986.
19. Raimund Seidel. Linear programming and convex hulls made easy. in Pro~’. 6~J’ ACM Symposium on Computational Geometry, pages 211-215, 1990.
20. Michael lan Shamos and Franco P. Preparata. Computational Geometry: an lntrodu~tion. Springer-Verlag, 1985.
21. Seth J. Teller and Michael E. Hohmeyer. Stabbing oriented convex polygons in randomized O(~2) time ~in preparation).
22. Gert Vegter. The visibility diagram: a data structure for visibility problems and motion planning. In Pro~. 2”’t S~andinavian ~wkshop tm Algorithm Theory, pages 97-11(), 1990.