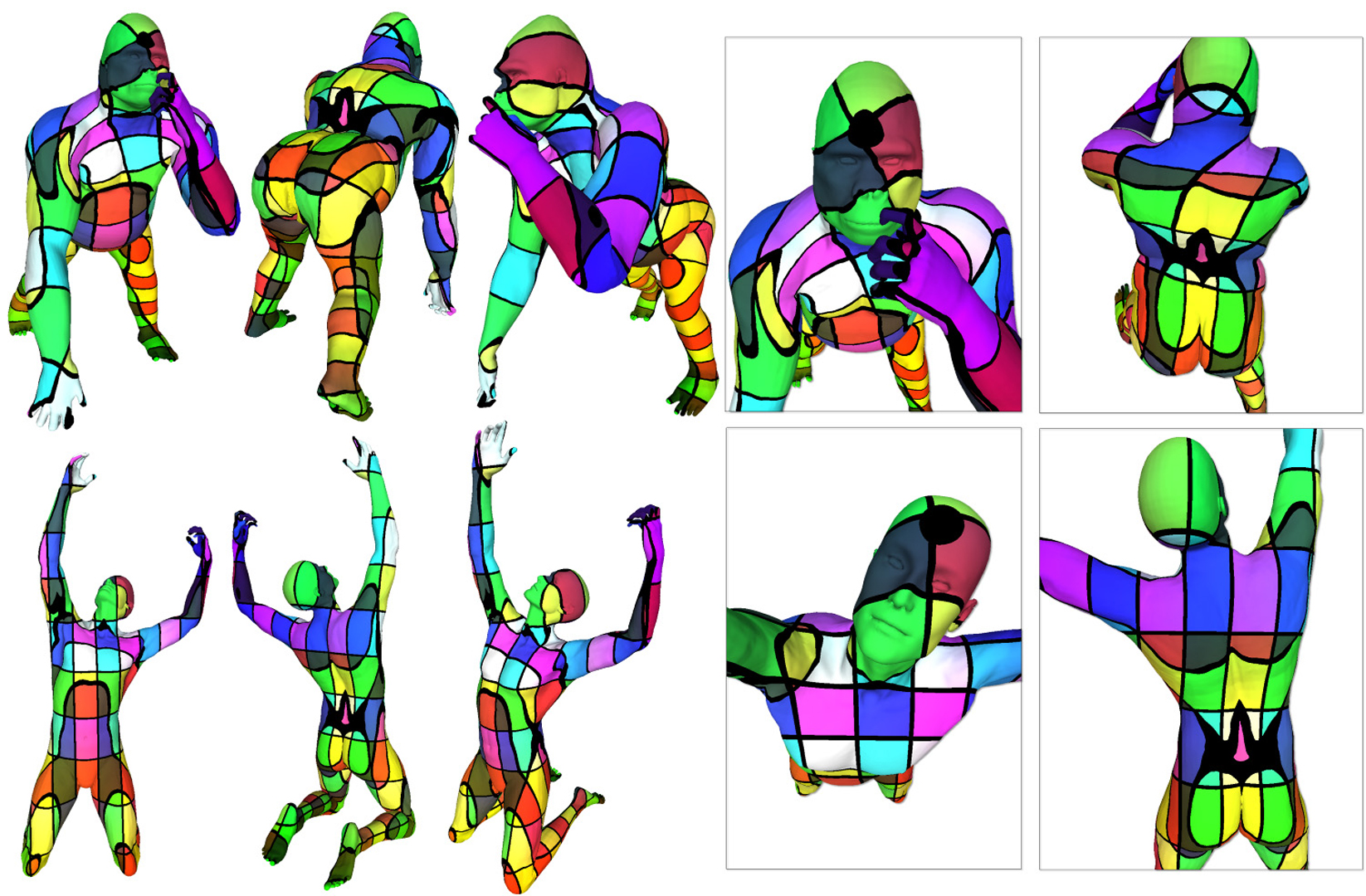
“Variance-minimizing transport plans for inter-surface mapping” by Mandad, Cohen-Steiner, Kobbelt, Alliez and Desbrun
Conference:
Type(s):
Title:
- Variance-minimizing transport plans for inter-surface mapping
Session/Category Title: Mappings and Deformations
Presenter(s)/Author(s):
Moderator(s):
Abstract:
We introduce an efficient computational method for generating dense and low distortion maps between two arbitrary surfaces of same genus. Instead of relying on semantic correspondences or surface parameterization, we directly optimize a variance-minimizing transport plan between two input surfaces that defines an as-conformal-as-possible inter-surface map satisfying a user-prescribed bound on area distortion. The transport plan is computed via two alternating convex optimizations, and is shown to minimize a generalized Dirichlet energy of both the map and its inverse. Computational efficiency is achieved through a coarse-to-fine approach in diffusion geometry, with Sinkhorn iterations modified to enforce bounded area distortion. The resulting inter-surface mapping algorithm applies to arbitrary shapes robustly, with little to no user interaction.
References:
1. Yonathan Aflalo, Ron Kimmel, and Michael Zibulevsky. 2013. Conformal Mapping with as Uniform as Possible Conformal Factor. SIAM J. Imaging Sciences 6, 1 (2013), 78–101. Google ScholarCross Ref
2. Noam Aigerman and Yaron Lipman. 2015. Orbifold Tutte embeddings. ACM Trans. Graph. 34, 6 (2015), Art. 190. Google ScholarDigital Library
3. Noam Aigerman, Roi Poranne, and Yaron Lipman. 2014. Lifted bijections for low distortion surface mappings. ACM Trans. Graph 33, 4 (2014), Art. 69. Google ScholarDigital Library
4. Noam Aigerman, Roi Poranne, and Yaron Lipman. 2015. Seamless surface mappings. ACM Trans. Graph. 34, 4 (2015), Art. 72. Google ScholarDigital Library
5. Dragomir Anguelov, Praveen Srinivasan, Hoi-Cheung Pang, Daphne Koller, Sebastian Thrun, and James Davis. 2004. The Correlated Correspondence Algorithm for Unsupervised Registration of Nonrigid Surfaces. In Proc. of Neural Information Processing Systems (NIPS). 33–40.Google Scholar
6. Arul Asirvatham, Emil Praun, and Hugues Hoppe. 2005. Consistent Spherical Parameterization. In Int. Conf. Computational Science. Springer, 265–272. Google ScholarDigital Library
7. Heinz H. Bauschke and Adrian S. Lewis. 1998. Dykstra’s algorithm with Bregman projections: a convergence proof. Optimization 48 (1998), 409–427. Google ScholarCross Ref
8. Jean-David Benamou, Guillaume Carlier, Marco Cuturi, Luca Nenna, and Gabriel Peyré. 2015. Iterative Bregman Projections for Regularized Transportation Problems. SIAM J. Scient. Comp. 37, 2 (2015). Google ScholarCross Ref
9. Davide Boscaini, Jonathan Masci, Emanuele Rodolà, and Michael M. Bronstein. 2016. Learning Shape Correspondence with Anisotropic Convolutional Neural Networks. In Proceedings of Neural Information Processing Systems (NIPS).Google Scholar
10. Alexander Bronstein, Michael Bronstein, and Ron Kimmel. 2008. Numerical Geometry of Non-Rigid Shapes (1 ed.). Springer.Google Scholar
11. Alexander M. Bronstein, Michael M. Bronstein, and Ron Kimmel. 2006. Generalized multidimensional scaling: A framework for isometry-invariant partial surface matching. Proceedings of the National Academy of Sciences 103, 5 (2006), 1168–1172. Google ScholarCross Ref
12. CGAL Project. 2016. CGAL User and Reference Manual (4.8 ed.). CGAL Editorial Board. http://doc.cgal.org/4.8/Manual/packages.htmlGoogle Scholar
13. Qifeng Chen and Vladlen Koltun. 2015. Robust Nonrigid Registration by Convex Optimization. In Proceedings of ICCV. 2039–2047. Google ScholarDigital Library
14. Lenaic Chizat, Gabriel Peyré, Bernhard Schmitzer, and François-Xavier Vialard. 2015. Unbalanced Optimal Transport: Geometry and Kantorovich Formulation. (2015). http://arxiv.org/abs/1508.05216Google Scholar
15. Lenaic Chizat, Gabriel Peyré, Bernhard Schmitzer, and François-Xavier Vialard. 2016. Scaling Algorithms for Unbalanced Transport Problems. (2016). https://arxiv.org/abs/1607.05816Google Scholar
16. Ronald R. Coifman, Stéphane Lafon, Ann B. Lee, Mauro Maggioni, F Frederick J. Warner, and Steven W. Zucker. 2005. Geometric diffusions as a tool for harmonic analysis and structure definition of data: Diffusion maps. In National Academy of Sciences, Vol. 102(21). 7426–7431.Google ScholarCross Ref
17. Etienne Corman, Maks Ovsjanikov, and Antonin Chambolle. 2015. Continuous Matching via Vector Field Flow. Comput. Graph. Forum 34, 5 (2015), 129–139.Google ScholarCross Ref
18. Marco Cuturi. 2013. Sinkhorn Distances: Lightspeed Computation of Optimal Transport. Adv. Neural Inf. Process. Syst. 26 (2013), 2292–2300.Google Scholar
19. Charlie Frogner, Chiyuan Zhang, Hossein Mobahi, Mauricio Araya-Polo, and Tomaso Poggio. 2015. Learning with a Wasserstein Loss. In Proceedings of Neural Information Processing Systems (NIPS). 2053–2061.Google Scholar
20. S. Gallot, G. Besson, and P. Bérard. 1994. Embedding Riemannian Manifolds by Their Heat Kernel. Geom. Funct. Anal. 4, 4 (1994), 373–398. Google ScholarCross Ref
21. Daniela Giorgi, Silvia Biasotti, and Laura Paraboschi. 2007. Shape retrieval contest 2007: Watertight models track. SHREC competition 8 (2007).Google Scholar
22. Vladimir G. Kim, Yaron Lipman, and Thomas A. Funkhouser. 2011. Blended intrinsic maps. ACM Trans. Graph 30, 4 (2011), Art. 79. Google ScholarDigital Library
23. Vladislav Kraevoy and Alla Sheffer. 2004. Cross-parameterization and Compatible Remeshing of 3D Models. In Proceedings of ACM SIGGRAPH, Vol. 23(3). 861–869. Google ScholarDigital Library
24. Yaron Lipman. 2012. Bounded distortion mapping spaces for triangular meshes. ACM Trans. Graph. 31, 4 (2012), Art. 108. Google ScholarDigital Library
25. Facundo Mémoli. 2011. Gromov-Wasserstein Distances and the Metric Approach to Object Matching. Foundations of Computational Mathematics 11, 4 (2011), 417–487. Google ScholarDigital Library
26. Ashish Myles and Denis Zorin. 2013. Controlled-distortion constrained global parametrization. ACM Trans. Graph. 32, 4 (2013), 105:1–105:14.Google ScholarDigital Library
27. Boaz Nadler, Stephane Lafon, Ioannis Kevrekidis, and Ronald R. Coifman. 2005. Diffusion Maps, Spectral Clustering and Eigenfunctions of Fokker-Planck Operators. Appl. Comput. Harmon. Anal. 21, 1 (2005), 113 — 127. Google ScholarCross Ref
28. Maks Ovsjanikov, Mirela Ben-Chen, Justin Solomon, Adrian Butscher, and Leonidas J. Guibas. 2012. Functional maps: a flexible representation of maps between shapes. ACM Trans. Graph. 31, 4 (2012), Art. 30. Google ScholarDigital Library
29. Yixuan Qiu, Gael Guennebaud, and Jitse Niesen. 2016. Spectra: A header-only C++ library for large scale eigenvalue problems. (2016). http://yixuan.cos.name/spectra/Google Scholar
30. Anand Rangarajan, Alan L. Yuille, and Eric Mjolsness. 1999. Convergence Properties of the Softassign Quadratic Assignment Algorithm. Neural Computation 11, 6 (1999), 1455–1474. Google ScholarDigital Library
31. Emanuele Rodolà, Michael Moeller, and Daniel Cremers. 2015. Point-wise Map Recovery and Refinement from Functional Correspondence. In Proceedings of VMV. 25–32.Google Scholar
32. Bernhard Schmitzer. 2016. Scaling Algorithms for Unbalanced Transport Problems. (2016). https://arxiv.org/abs/1610.06519Google Scholar
33. John Schreiner, Arul Asirvatham, Emil Praun, and Hugues Hoppe. 2004. Inter-surface Mapping. In Proceedings of ACM SIGGRAPH. 870–877. Google ScholarDigital Library
34. Alon Shtern and Ron Kimmel. 2015. Spectral gradient fields embedding for nonrigid shape matching. Computer Vision and Image Understanding 140 (2015), 21–29. Google ScholarDigital Library
35. Richard Sinkhorn. 1964. A Relationship Between Arbitrary Positive Matrices and Doubly Stochastic Matrices. Annals Math. Statist. 35 (1964). Google ScholarCross Ref
36. Justin Solomon, Fernando de Goes, Gabriel Peyré, Marco Cuturi, Adrian Butscher, Andy Nguyen, Tao Du, and Leonidas Guibas. 2015. Convolutional Wasserstein Distances: Efficient Optimal Transportation on Geometric Domains. ACM Trans. Graph. 34, 4 (2015). Google ScholarDigital Library
37. Justin Solomon, Leonidas J. Guibas, and Adrian Butscher. 2013. Dirichlet Energy for Analysis and Synthesis of Soft Maps. Comp. Graph. Forum 32, 5 (2013), 197–206.Google ScholarDigital Library
38. Justin Solomon, Andy Nguyen, Adrian Butscher, Mirela Ben-Chen, and Leonidas J. Guibas. 2012. Soft Maps Between Surfaces. Comp. Graph. Forum 31, 5 (2012), 1617–1626.Google ScholarDigital Library
39. Justin Solomon, Gabriel Peyré, Vladimir G. Kim, and Suvrit Sra. 2016. Entropic Metric Alignment for Correspondence Problems. ACM Trans. Graph. 35, 4 (2016), Art. 72. Google ScholarDigital Library
40. Jian Sun, Maks Ovsjanikov, and Leonidas Guibas. 2009. A Concise and Provably Informative Multi-scale Signature Based on Heat Diffusion. In Symposium on Geometry Processing. 1383–1392. Google ScholarCross Ref
41. Oliver van Kaick, Hao Zhang, Ghassan Hamarneh, and Daniel Cohen-Or. 2011. A Survey on Shape Correspondence. Comp. Graph. Forum 30, 6 (2011), 1681–1707.Google ScholarCross Ref
42. Matthias Vestner, Roee Litman, Emanuele Rodolà, Alex Bronstein, and Daniel Cremers. 2017. Product Manifold Filter: Non-rigid shape correspondence via kernel density estimation in the product space. In Proceedings of CVPR.Google ScholarCross Ref