“True2Form: 3D curve networks from 2D sketches via selective regularization” by Xu, Chang, Sheffer, Singh, Bousseau, et al. …
Conference:
Type(s):
Title:
- True2Form: 3D curve networks from 2D sketches via selective regularization
Session/Category Title: Interactive Modeling
Presenter(s)/Author(s):
Moderator(s):
Abstract:
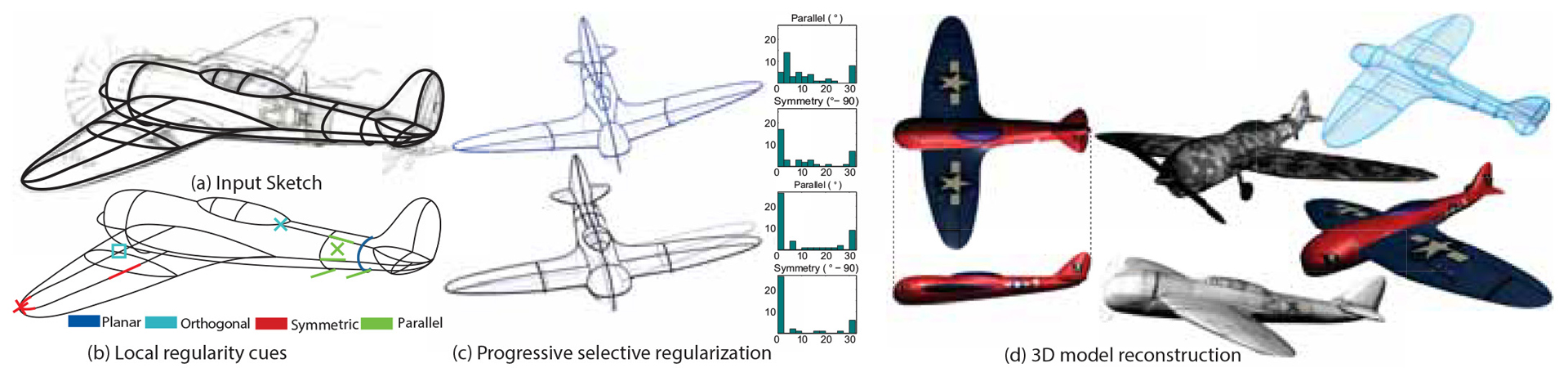
True2Form is a sketch-based modeling system that reconstructs 3D curves from typical design sketches. Our approach to infer 3D form from 2D drawings is a novel mathematical framework of insights derived from perception and design literature. We note that designers favor viewpoints that maximally reveal 3D shape information, and strategically sketch descriptive curves that convey intrinsic shape properties, such as curvature, symmetry, or parallelism. Studies indicate that viewers apply these properties selectively to envision a globally consistent 3D shape. We mimic this selective regularization algorithmically, by progressively detecting and enforcing applicable properties, accounting for their global impact on an evolving 3D curve network. Balancing regularity enforcement against sketch fidelity at each step allows us to correct for inaccuracy inherent in free-hand sketching. We perceptually validate our approach by showing agreement between our algorithm and viewers in selecting applicable regularities. We further evaluate our solution by: reconstructing a range of 3D models from diversely sourced sketches; comparisons to prior art; and visual comparison to both ground-truth and 3D reconstructions by designers.
References:
1. Andre, A., and Saito, S. 2011. Single-view sketch based modeling. In Proc. Sketch-Based Interfaces and Modeling. Google ScholarDigital Library
2. Bae, S., Balakrishnan, R., and Singh, K. 2008. ILoveSketch: as-natural-as-possible sketching system for creating 3d curve models. In Proc. User Interface Software and Technology. Google ScholarDigital Library
3. Bessmeltsev, M., Wang, C., Sheffer, A., and Singh, K. 2012. Design-driven quadrangulation of closed 3d curves. ACM Trans. Graph. 31, 5. Google ScholarDigital Library
4. Bommes, D., Zimmer, H., and Kobbelt, L. 2009. Mixed-integer quadrangulation. ACM Transactions on Graphics (Proc. SIGGRAPH) 28, 3, 77:1–77:10. Google ScholarDigital Library
5. Bordegoni, M., and Rizzi, C. 2011. Innovation in Product Design: From CAD to Virtual Prototyping. Springer.Google Scholar
6. Chen, T., Zhu, Z., Shamir, A., Hu, S.-M., and Cohen-Or, D. 2013. 3-sweep: Extracting editable objects from a single photo. ACM Trans. Graphics 32, 6. Google ScholarDigital Library
7. Cooper, M. 2008. Line Drawing Interpretation. Springer. Google ScholarDigital Library
8. Eissen, K., and Steur, R. 2011. Sketching: The Basics. Bis Publishers.Google Scholar
9. Gingold, Y., Igarashi, T., and Zorin, D. 2009. Structured annotations for 2D-to-3D modeling. ACM Trans. Graph. 28, 5. Google ScholarDigital Library
10. Igarashi, T., Matsuoka, S., and Tanaka, H. 1999. Teddy: a sketching interface for 3D freeform design. Proc. SIGGRAPH. Google ScholarDigital Library
11. Kara, L. B., and Shimada, K. 2007. Sketch-based 3d-shape creation for industrial styling design. IEEE Comput. Graph. Appl. 27, 1, 60–71. Google ScholarDigital Library
12. Knill, D. C. 1992. Perception of surface contours and surface shape: from computation to psychophysics. Journal of Optical Society of America 9, 9, 1449–1464.Google ScholarCross Ref
13. Koffka, K. 1955. Principles of Gestalt Psychology. International library of psychology, philosophy, and scientific method. Routledge & K. Paul.Google Scholar
14. Lau, M., Saul, G., Mitani, J., and Igarashi, T. 2010. Modeling-in-context: user design of complementary objects with a single photo. In Proc. Sketch-Based Interfaces and Modeling, 17–24. Google ScholarDigital Library
15. Lee, S., Feng, D., and Gooch, B. 2008. Automatic construction of 3d models from architectural line drawings. In Proc. Interactive 3D graphics & games, 123–130. Google ScholarDigital Library
16. Li, Y., Wu, X., Chrysanthou, Y., Sharf, A., Cohen-Or, D., and Mitra, N. J. 2011. GlobFit: Consistently fitting primitives by discovering global relations. ACM Trans. Graph. 30, 4. Google ScholarDigital Library
17. Lipson, H., and Shpitalni, M. 1996. Optimization-based reconstruction of a 3d object from a single freehand line drawing. Computer-Aided Design 28, 651–663.Google ScholarCross Ref
18. Lowe, D. G. 1987. Three-dimensional object recognition from single two-dimensional images. Artif. Intell. 31, 3, 355–395. Google ScholarDigital Library
19. Malik, J. 1987. Interpreting line drawings of curved objects. International Journal of Computer Vision 1, 1, 73–103.Google ScholarDigital Library
20. Mamassian, P., and Landy, M. S. 1998. Observer biases in the 3D interpretation of line drawings. Vision research 38, 18, 2817–2832.Google Scholar
21. Mather, G. 2008. Foundations of sensation and perception. Taylor and Francis.Google Scholar
22. McCrae, J., Singh, K., and Mitra, N. 2011. Slices: a shape-proxy based on planar sections. ACM Trans. Graph. 30, 6. Google ScholarDigital Library
23. Nakayama, K., and Shimojo, S. 1992. Experiencing and Perceiving Visual Surfaces. Science 257, 1357–1363.Google ScholarCross Ref
24. Nealen, A., Igarashi, T., Sorkine, O., and Alexa, M. 2007. Fibermesh: designing freeform surfaces with 3d curves. ACM Trans. Graph. 26. Google ScholarDigital Library
25. Olsen, L., Samavati, F., Sousa, M., and Jorge, J. 2009. Sketch-based modeling: A survey. Computers & Graphics 33. Google ScholarDigital Library
26. Olsen, L., Samavati, F., and Jorge, J. A. 2011. Naturasketch: Modeling from images and natural sketches. IEEE Computer Graphics and Applications 31, 6, 24–34. Google ScholarDigital Library
27. Orbay, G., and Kara, L. B. 2012. Sketch-based surface design using malleable curve networks. Computers & Graphics 36, 8, 916–929. Google ScholarDigital Library
28. Perkins, D. 1971. Cubic corners, oblique views of pictures, the perception of line drawings of simple space forms. geometry and the perception of pictures: Three studies. Tech. rep., Harvard Univ., Cambridge, MA. Graduate School of Education.Google Scholar
29. Pipes, A. 2007. Drawing for Designers. Laurence King.Google Scholar
30. Pizlo, Z., and Stevenson, A. 1999. Shape constancy from novel views. Perception & Psychophysics 61, 7, 1299–1307.Google ScholarCross Ref
31. Schmidt, R., Khan, A., Kurtenbach, G., and Singh, K. 2009. On expert performance in 3D curve-drawing tasks. In Proc. Sketch-Based Interfaces and Modeling. Google ScholarDigital Library
32. Schmidt, R., Khan, A., Singh, K., and Kurtenbach, G. 2009. Analytic drawing of 3d scaffolds. ACM Trans. Graph. 28, 5. Google ScholarDigital Library
33. Shao, C., Bousseau, A., Sheffer, A., and Singh, K. 2012. Crossshade: Shading concept sketches using cross-section curves. ACM Trans. Graphics 31, 4. Google ScholarDigital Library
34. Sharf, A., Alcantara, D. A., Lewiner, T., Greif, C., Sheffer, A., Amenta, N., and Cohen-Or, D. 2008. Space-time surface reconstruction using incompressible flow. ACM Trans. Graph. 27, 5, 110:1–110:10. Google ScholarDigital Library
35. Shtof, A., Agathos, A., Gingold, Y., Shamir, A., and Cohen-Or, D. 2013. Geosemantic snapping for sketch-based modeling. Computer Graphics Forum 32, 2, 245–253.Google ScholarCross Ref
36. Stevens, K. A. 1981. The visual interpretation of surface contours. Artificial Intelligence 17.Google Scholar
37. Sýkora, D., Kavan, L., Čadík, M., Jamriška, O., Jacobson, A., Whited, B., Simmons, M., and Sorkine-Hornung, O. 2014. Ink-and-ray: Bas-relief meshes for adding global illumination effects to hand-drawn characters. ACM Trans. Graphics 33. Google ScholarDigital Library
38. Tian, C., Masry, M., and Lipson, H. 2009. Physical sketching: Reconstruction and analysis of 3D objects from freehand sketches. Computer Aided Design 41, 3, 147–158. Google ScholarDigital Library
39. Wang, Y., Chen, Y., Liu, J., and Tang, X. 2009. 3D reconstruction of curved objects from single 2D line drawings. IEEE Computer Vision and Pattern Recognition 0, 1834–1841.Google Scholar
40. Zhuang, Y., Zou, M., Carr, N., and Ju, T. 2013. A general and efficient method for finding cycles in 3d curve networks. ACM Trans. Graph. 32, 6. Google ScholarDigital Library