“The haloed line effect for hidden line elimination.” by Appel, Rohlf and Stein

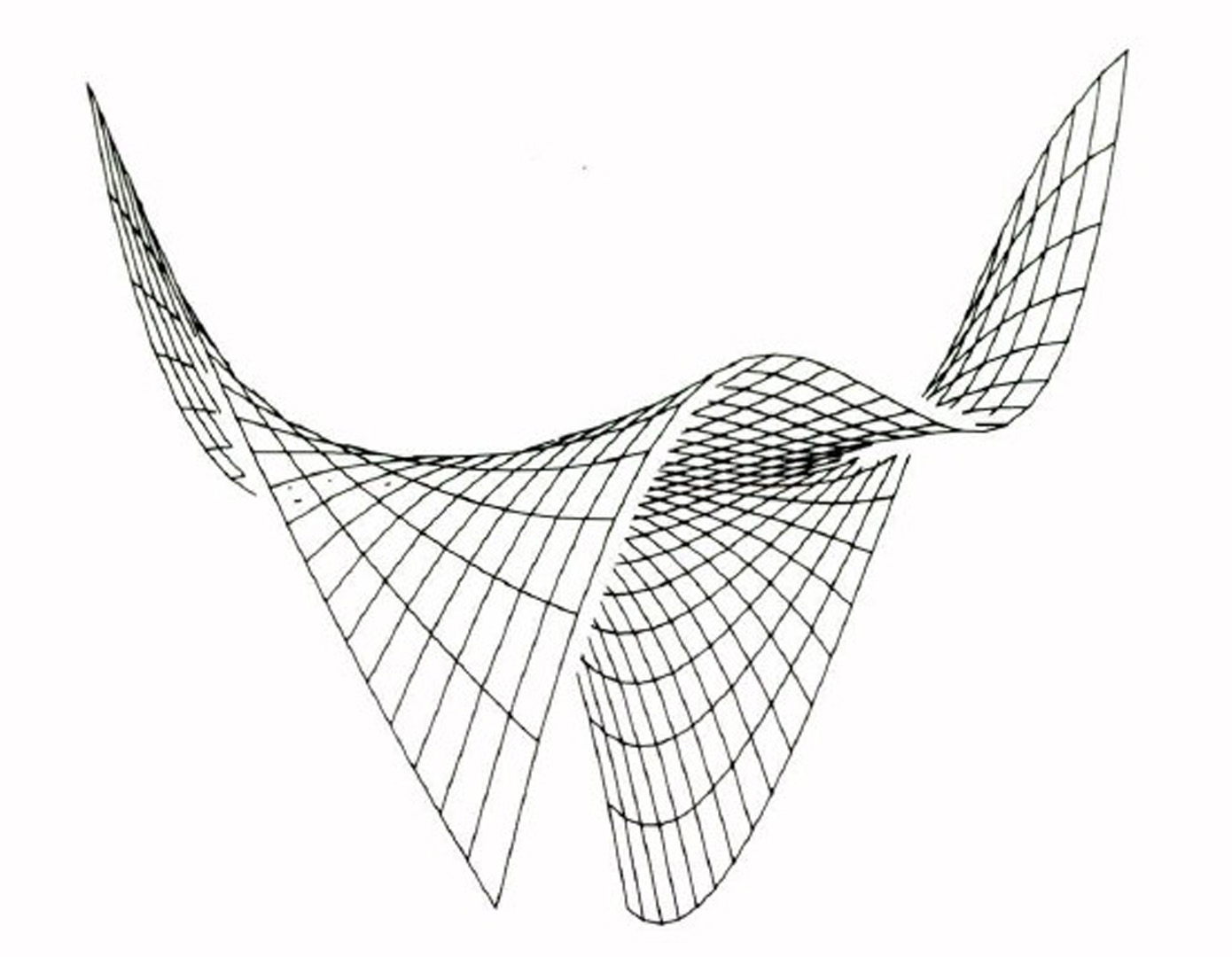
The haloed line effect is a technique where when a line in three-dimensional space passes in front of another line, a gap is produced in the projection of the more distant line. The gap is produced as if an opaque halo surrounded the closer line. This method for approximate hidden-line-elimination is advantageous because explicit surface equations are not necessary. The relative depth of lines, axes, curves and lettering is easily perceived. This technique is especially suitable for the display of finite element grids, three-dimensional contour maps and ruled surfaces. When the lines or curves on a surface are closer than the gap size, the gaps produced close up to produce a complete hidden-line-elimination. A simple but efficient implementation is described which can be used in the rendering of a variety of three-dimensional situations.

1. J. Encarnacao, “Survey of and New Solutions for the Hidden-Line Problem”, PROCEEDING OF SYMPOSIUM ON COMPUTER GRAPHICS, Delft, Netherlands, October 1970, pp. 26-28.
2. I. E. Sutherland, R. F. Sproull and R. A. Schumacker, “A Characterization of Ten Hidden-Surface Algorithms”, COMPUTING SURVEYS, Vol. 6, No. 1, March 1974, pp. 1-55.
3. Various techniques are discussed in Chapter 5 of Wolfgang K. Giloi, INTERACTIVE COMPUTER GRAPHICS, Prentice-Hall Inc, Englewood Cliffs, N. J., 1978.
4. Various techniques are discussed in Chapter 14 of William M. Newman and Robert F. Sproull, PRINCIPLES OF INTERACTIVE COMPUTER GRAPHICS, McGraw-Hill Book Company, New York, 1973.
5. J. G. Griffiths, “Bibliography of Hidden-Line and Hidden Surface Algorithms”, COMPUTER-AIDED DESIGN, Vol. 10, No. 3, May 1978, pp. 203-206.
6. C. Wylie, G. W. Romney, D. C. Evans, and A. Erdahl, “Halftone Perspective Drawings by Computer”, PROC. AFIPS FJCC 1976, Vol. 31, 49.
7. A. Appel, “Hidden Line Elimination for Complex Surfaces”, IBM TECHNICAL DISCLOSURE BULLETIN, Vol. 18, No. 11, April 1976, pp. 3873-3876.
8. Bruce G. Baumgart, “A Polyhedron Representation for Computer Vision”, PROCEEDINGS AFIPS NATIONAL COMPUTER CONFERENCE 1975, Vol. 44, pp. 589-596.
9. L. I. Lieberman, M. A. Wesley, M. A. Lavin, “A GEOMETRIC MODELLING SYSTEM FOR AUTOMATED MECHANICAL ASSEMBLY,” IBM Research Report RC 7089, April 25, 1978.
10. Ruth A. Weiss, “BE VISION: a package of IBM 7090 Fortran programs to draw orthographic views of combinations of plane and quadratic surfaces”, JOURNAL OF THE ACM, Vol. 13, No. 2, April 1966, pp. 194-204.
11. Peter Woon and Herbert Freeman, “A Procedure for Generating Visible Line Projections of Solids Bounded by Quadric Surfaces”, PROCEEDINGS IFIP CONGRESS INFORMATION PROCESSING, North Holland, 1971, pp. 1120-1125.
12. Thomas J. Wright, “A Two-Spaced Solution to the Hidden Line Problem for Plotting Functions of Two Variables”, IEEE TRANS. ON COMPUTERS, Vol. c-22, No. 1, January 1973, pp. 28-33.
13. A. Appel, S. W. Handelman and A. J. Stein, “Hidden Line Elimination for Semi-Convex Slices”, IBM TECHNICAL DISCLOSURE BULLETIN, Vol. 20, No. 7, December 1977, pp. 2917-2920.
14. Wm. Randolph Franklin and Harry R. Lewis, “3-D Graphic Display of Discrete Spatial Data by Prism Maps”, Computer Graphics, Vol. 12, No. 3, August 1978, Quarterly Report of SIGGRAPH-ACM. pp. 70-75.
15. Thomas Wright, “Visible Surface Plotting Program”, COMMUNICATIONS OF THE ACM, Vol. 17, No. 3, March 1974, pp. 152-155.
16. A. Appel and A. J. Stein, “Cellular Automata for Hidden-Line Elimination”, IBM TECHNICAL DISCLOSURE BULLETIN, Vol. 17, No. 2, July 1974, pp. 586-589.
17. I.E. Sutherland and R. F. Sproull, “A Clipping Divider,” Proc. AFIPS FJCC 1968 Conference, Vol. 33, Part I, pp. 765-776.
18. James F. Blinn and Martin E. Newell, “Clipping using Homogeneous Coordinates”, Computer Graphics, Quarterly Report of SIGGRAPH-ACM, Vol. 12, No. 3, August 1978, pp. 245-251.
19. A. Appel, “The Notion of Quantitative Invisibility and the Machine Rendering of Solids”, Proc. ACM National Conference 1967, pp. 387-393.