“Terrain generation using procedural models based on hydrology” by Génevaux, Galin, Guerin, Peytavie and Benes
Conference:
Type(s):
Title:
- Terrain generation using procedural models based on hydrology
Session/Category Title: Laplacians, Light Field & Layouts
Presenter(s)/Author(s):
Moderator(s):
Abstract:
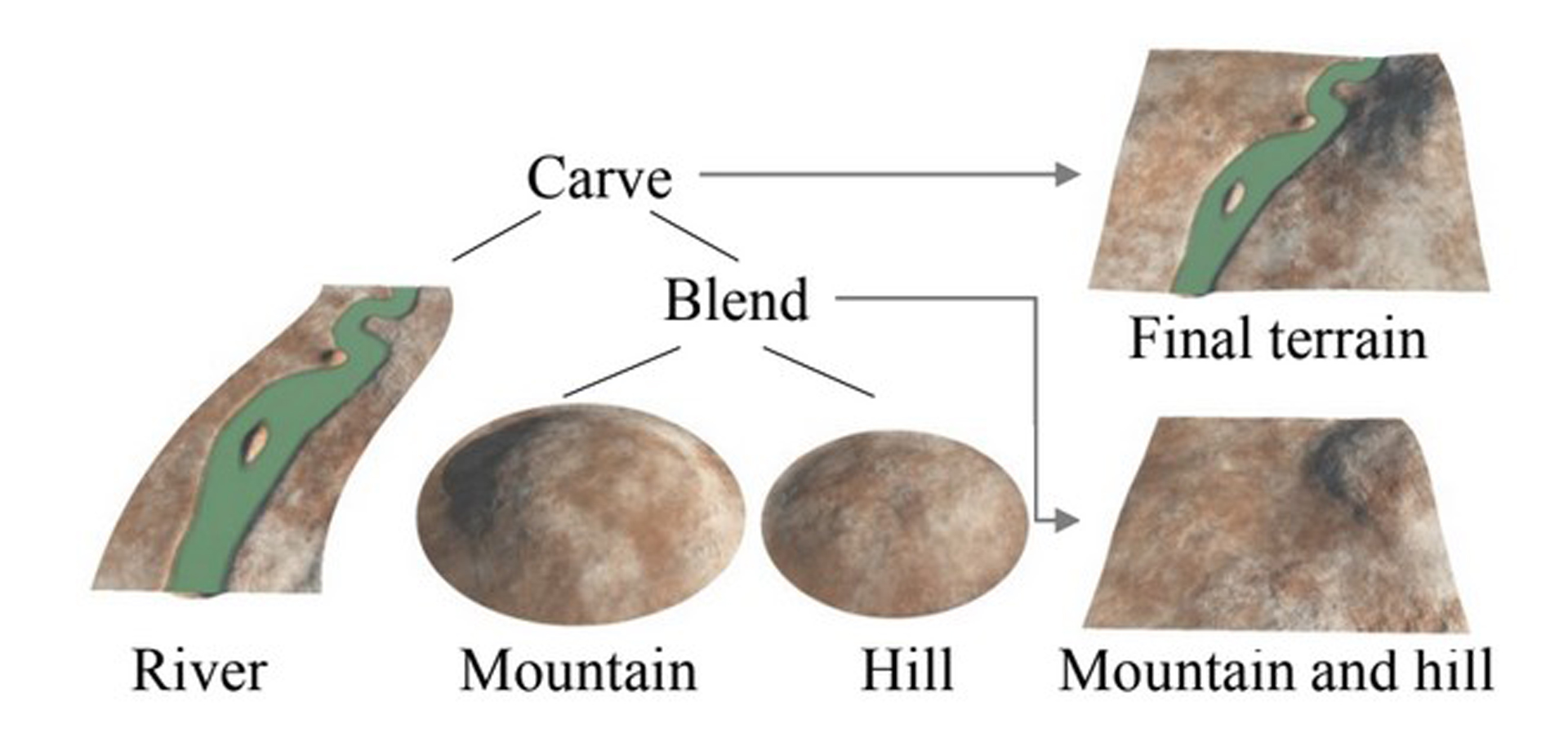
We present a framework that allows quick and intuitive modeling of terrains using concepts inspired by hydrology. The terrain is generated from a simple initial sketch, and its generation is controlled by a few parameters. Our terrain representation is both analytic and continuous and can be rendered by using varying levels of detail. The terrain data are stored in a novel data structure: a construction tree whose internal nodes define a combination of operations, and whose leaves represent terrain features. The framework uses rivers as modeling elements, and it first creates a hierarchical drainage network that is represented as a geometric graph over a given input domain. The network is then analyzed to construct watersheds and to characterize the different types and trajectories of rivers. The terrain is finally generated by combining procedural terrain and river patches with blending and carving operators.
References:
1. Belhadj, F., and Audibert, P. 2005. Modeling landscapes with ridges and rivers: bottom up approach. In GRAPHITE, 447–450. Google ScholarDigital Library
2. Beneš, B., and Forsbach, R. 2001. Layered data representation for visual simulation of terrain erosion. In Proc. of the Spring Conf. on Comp. Graphics, 80–85. Google ScholarDigital Library
3. Beneš, B., and Forsbach, R. 2002. Visual simulation of hydraulic erosion. In Journal of WSCG, vol. 10, 79–86.Google Scholar
4. Beneš, B., Těšínský, V., Hornyš, J., and Bhatia, S. 2006. Hydraulic erosion. Comp. Anim. Virt. Worlds 17, 2, 99–108. Google ScholarDigital Library
5. Chiba, N., Muraoka, K., and Fujita, K. 1998. An erosion model based on velocity fields for the visual simulation of mountain scenery. Journal of Vis. and Comp. Anim. 9, 4, 185–194.Google ScholarCross Ref
6. Derzapf, E., Ganster, B., Guthe, M., and Klein, R. 2011. River networks for instant procedural planets. Comput. Graph. Forum 30, 7, 2031–2040.Google ScholarCross Ref
7. Dodd, P., and Rothman, D. 2000. Scaling, universality, and geomorphology. Annual Review of Earth and Planetary Sciences 28, 571610.Google Scholar
8. Dunne, T., and Leopold, L. B. 1978. Water in Environmental Planning. W. H. Freeman.Google Scholar
9. Ebert, D., Musgrave, K., Peachey, D., Perlin, K., and Worley, S. 1998. Texturing and Modeling: A Procedural Approach. Academic Press Professional. Google ScholarDigital Library
10. Fournier, A., Fussell, D., and Carpenter, L. 1982. Comp. rendering of stochastic models. Comm. ACM 25, 6, 371–384. Google ScholarDigital Library
11. Gain, J., Marais, P., and Strasser, W. 2009. Terrain sketching. In Proc. of Interactive 3D graphics and games, 31–38. Google ScholarDigital Library
12. Hnaidi, H., Guérin, E., Akkouche, S., Peytavie, A., and Galin, E. 2010. Feature based terrain generation using diffusion equation. Comp. Grap. Forum 29, 7, 2179–2186.Google ScholarCross Ref
13. Horton, R. E. 1945. Erosional development of streams and their drainage basins: hydro-physical approach to quantitative morphology. Geological Society of America Bulletin 56, 3, 275370.Google ScholarCross Ref
14. Kelley, A., Malin, M., and Nielson, G. 1988. Terrain simulation using a model of stream erosion. In Computer Graphics 22, 4, 263–268. Google ScholarDigital Library
15. Krištof, P., Beneš, B., Křivánek, J., and Štava, O. 2009. Hydraulic erosion using smoothed particle hydrodynamics. Comp. Grap. Forum 28, 2, 219–228.Google ScholarCross Ref
16. Lagae, A., and Dutré, P. 2005. A procedural object distribution function. ACM Trans. Graph. 24, 4 (Oct.), 1442–1461. Google ScholarDigital Library
17. Mei, X., Decaudin, P., and Hu, B. 2007. Fast hydraulic erosion simulation and visualization on GPU. In Pacific Graphics, 47–56. Google ScholarDigital Library
18. Musgrave, F. K., Kolb, C. E., and Mace, R. S. 1989. The synthesis and rendering of eroded fractal terrains. In Computer Graphics 23, 3, 41–50. Google ScholarDigital Library
19. Nagashima, K. 1998. Computer generation of eroded valley and mountain terrains. The Visual Computer 13, 9–10, 456–464.Google ScholarCross Ref
20. Perlin, K. 1985. An image synthesizer. In Computer Graphics 19, 3, 287–296. Google ScholarDigital Library
21. Peytavie, A., Galin, E., Merillou, S., and Grosjean, J. 2009. Arches: a Framework for Modeling Complex Terrains. Comp. Grap. Forum 28, 2, 457–467.Google ScholarCross Ref
22. Prusinkiewicz, P., and Hammel, M. 1993. A fractal model of mountains with rivers. In Graphics Interface, 174–180.Google Scholar
23. Rodriguez-Iturbe, I., and Rinaldo, A. 1997. Fractal River Basins: Chance and Self-Organization. Cambridge Univ. Press.Google Scholar
24. Rosgen, D. L. 1994. A classification of natural rivers. Catena 22, 169–199.Google ScholarCross Ref
25. Rusnell, B., Mould, D., and Eramian, M. G. 2009. Feature-rich distance-based terrain synthesis. The Visual Computer 25, 5–7, 573–579. Google ScholarDigital Library
26. Teoh, S. T. 2009. Riverland: An efficient procedural modeling system for creating realistic-looking terrains. In Proc. of the Int. Symp. on Advances in Visual Computing: Part I, 468–479. Google ScholarDigital Library
27. Vanek, J., Beneš, B., Herout, A., and Štava, O. 2011. Large-scale physics-based terrain editing using adaptive tiles on the GPU. Comp. Graphics and App., IEEE 31, 6, 35–44. Google ScholarDigital Library
28. Štava, O., Beneš, B., Brisbin, M., and Křivá nek, J. 2008. Interactive terrain modeling using hydraulic erosion. In Symposium on Computer Animation, 201–210. Google ScholarDigital Library
29. Wojtan, C., Carlson, M., Mucha, P., and Turk, G. 2007. Animating corrosion and erosion. In Proc. of the Eurographics Workshop on Natural Phenomena, 15–22. Google ScholarDigital Library
30. Wyvill, B., Guy, A., and Galin, E. 1999. Extending the csg tree – warping, blending and boolean operations in an implicit surface modeling system. Comp. Grap. Forum 18, 2, 149–158.Google ScholarCross Ref
31. Zhou, H., Sun, J., Turk, G., and Rehg, J. M. 2007. Terrain synthesis from digital elevation models. IEEE Transactions on Visualization and Computer Graphics 13, 4, 834–848. Google ScholarDigital Library