“Synthesizing physically realistic human motion in low-dimensional, behavior-specific spaces” by Safonova, Hodgins and Pollard

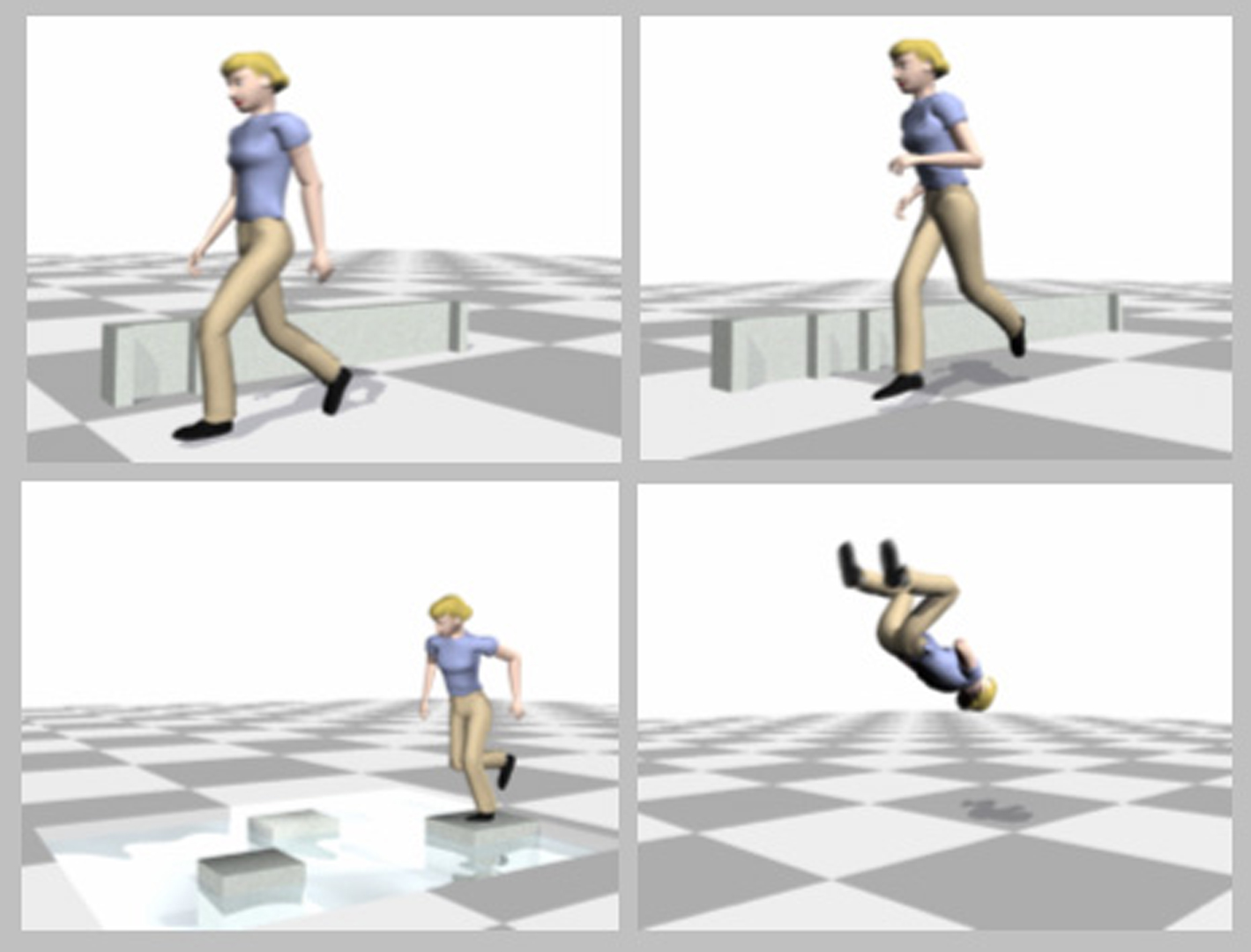
Optimization is an appealing way to compute the motion of an animated character because it allows the user to specify the desired motion in a sparse, intuitive way. The difficulty of solving this problem for complex characters such as humans is due in part to the high dimensionality of the search space. The dimensionality is an artifact of the problem representation because most dynamic human behaviors are intrinsically low dimensional with, for example, legs and arms operating in a coordinated way. We describe a method that exploits this observation to create an optimization problem that is easier to solve. Our method utilizes an existing motion capture database to find a low-dimensional space that captures the properties of the desired behavior. We show that when the optimization problem is solved within this low-dimensional subspace, a sparse sketch can be used as an initial guess and full physics constraints can be enabled. We demonstrate the power of our approach with examples of forward, vertical, and turning jumps; with running and walking; and with several acrobatic flips.

1. ALBRO, J. V., SOHL, G. A., AND BOBROW, J. E. 2000. On the computation of optimal high-dives. In Proc. IEEE Intl. Conference on Robotics and Automation, 3958–3963.Google ScholarCross Ref
2. ANDERSON, F. C., AND PANDY, M. G. 1999. A dynamic optimization solution for vertical jumping in three dimensions. Computer Methods in Biomechanics and Biomedical Engineering, 2, 201–231.Google ScholarCross Ref
3. BRAND, M., AND HERTZMANN, A. 2000. Style machines. In Proc. of SIGGRAPH 2000, 183–192. Google ScholarDigital Library
4. CRAWFORD, L. S., AND SASTRY, S. S. 1995. Biological motor control approaches for a planar diver. In Proc. IEEE Conference on Decision and Control, 3881–3886.Google ScholarCross Ref
5. DASGUPTA, A., AND NAKAMURA, Y. 1999. Making feasible walking motion of humanoid robots from human motion capture data. In Proc. IEEE Intl. Conference on Robotics and Automation, 1044–1049.Google ScholarCross Ref
6. DE LA TORRE, F., AND BLACK, M. J. 2003. A framework for robust subspace learning. In Intl. Journal of Computer Vision, vol. 54, 117–142. Google ScholarDigital Library
7. FANG, A. C., AND POLLARD, N. S. 2003. Efficient synthesis of physically valid human motion. ACM Trans. on Graphics 22, 3, 417–426. Google ScholarDigital Library
8. FOURER, R., GAY, D., AND KERNIGHAN, B., 1989. AMPL: A mathematical programming language.Google Scholar
9. FUKUNAGA, K. 1989. Statistical pattern recognition – 2nd edition. John Hopkins University Press, Baltimore. Google ScholarDigital Library
10. GILL, P. E., MURRAY, W., AND SAUNDERS, M. A. 1997. SNOPT: An SQP algorithm for large-scale constrained optimization. Tech. Rep. NA–97–2, San Diego, CA.Google Scholar
11. GLEICHER, M. 1997. Motion editing with spacetime constraints. In Proc. of the 1997 Symposium on Interactive 3D Graphics, 139–148. Google ScholarDigital Library
12. GRZESZCZUK, R., TERZOPOULOS, D., AND HINTON, G. 1998. Neuroanimator: Fast neural network emulation and control of physics-based models. In Proc. of SIGGRAPH 98, 9–20. Google ScholarDigital Library
13. HARDT, M. 1999. Multibody Dynamical Algorithms, Numerical Optimal Control, with Detailed Studies in the Control of Jet Engine Compressors and Biped Walking. PhD thesis, University of California San Diego. Google ScholarDigital Library
14. HUANG, G., LO, J., AND METAXAS, D. 2000. Human motion planning based on recurive dynamics and optimal control techniques. In Proc. of Computer Graphics International 2000, 19–28. Google ScholarDigital Library
15. JAMES, D. L., AND FATAHALIAN, K. 2003. Precomputing interactive dynamic deformable scenes. ACM Trans. on Graphics, 879–887. Google ScholarDigital Library
16. JENKINS, O. C., AND MATARIC, M. J. 2002. Deriving action and behavior primitives from human motion data. In IEEE/RSJ Intl. Conference on Intelligent Robots and Systems (IROS), 2551–2556.Google ScholarCross Ref
17. JOLLIFFE, I. 1986. Principal component analysis. Springer Verlag.Google Scholar
18. KO, H., AND BADLER, N. I. 1996. Animating human locomotion with inverse dynamics. In IEEE Computer Graphics and Applications, 50–59. Google ScholarDigital Library
19. KOREIN, J., AND BADLER, N. 1982. Techniques for generating the goal-directed motion of articulated structures. 71–81.Google Scholar
20. LALL, S. P., KRYSL, P., AND MARSDEN, J. E. 2003. Structure-preserving model reduction for mechanical systems. In Physica D 184, 304–318.Google ScholarCross Ref
21. LEE, J., AND SHIN, S. Y. 1999. A hierarchical approach to interactive motion editing for human-like figures. In Proc. of SIGGRAPH 99, 39–48. Google ScholarDigital Library
22. LI, Y., WANG, T., AND SHUM, H.-Y. 2002. Motion texture: a two-level statistical model for character motion synthesis. ACM Trans. on Graphics, 465–472. Google ScholarDigital Library
23. LIU, Z., AND COHEN, M. 1994. Decomposition of linked figure motion: Diving. In 5th Eurographics Workshop on Animation and Simulation.Google Scholar
24. LIU, Z., AND COHEN, M. F. 1995. Keyframe motion optimization by relaxing speed and timing. In 6th Eurographics Workshop on Animation and Simulation, 144–153.Google ScholarCross Ref
25. LIU, C. K., AND POPOVIĆ, Z. 2002. Synthesis of complex dynamic character motion from simple animations. ACM Trans. on Graphics 21, 3, 408–416. Google ScholarDigital Library
26. PANDY, M. G., AND ANDERSON, F. C. 2000. Dynamic simulation of human movement using large-scale models of the body. In Proc. IEEE Intl. Conference on Robotics and Automation, 676–681.Google ScholarCross Ref
27. PENTLAND, A., AND WILLIAMS, J. 1989. Good vibrations: Modal dynamics for graphics and animation. In Computer Graphics (Proc. of SIGGRAPH 89), vol. 23, 215–222. Google ScholarDigital Library
28. POLLARD, N. S., AND REITSMA, P. S. A. 2001. Animation of humanlike characters: Dynamic motion filtering with a physically plausible contact model. In Yale Workshop on Adaptive and Learning Systems.Google Scholar
29. POPOVIĆ, Z., AND WITKIN, A. P. 1999. Physically based motion transformation. In Proc. of SIGGRAPH 99, 11–20. Google ScholarDigital Library
30. POPOVIĆ, J., SEITZ, S. M., ERDMANN, M., POPOVIĆ, Z., AND WITKIN, A. P. 2000. Interactive manipulation of rigid body simulations. In Proc. of SIGGRAPH 00, 209–218. Google ScholarDigital Library
31. RAVINDRAN, S. 2000. Reduced-order adaptive controllers for fluid flows using POD. In Journal of Scientific Computing, vol. 15, 457–478. Google ScholarDigital Library
32. ROSE, C. F., GUENTER, B., BODENHEIMER, B., AND COHEN, M. F. 1996. Efficient generation of motion transitions using spacetime constraints. In Proc. of SIGGRAPH 96, 147–154. Google ScholarDigital Library
33. SANTELLO, M., FLANDERS, M., AND SOECHTING, J. F. 2002. Patterns of hand motion during grasping and the influence of sensory guidance. In Journal of Neuroscience, vol. 22, 1426–1435.Google ScholarCross Ref
34. SULEJMANPAŠIĆ, A. 2004. Adaptation of Performed Ballistic Motion. Master’s thesis, MIT Dept of EECS.Google Scholar
35. TOLANI, D., GOSWAMI, A., AND BADLER, N. 2000. Real-time inverse kinematics techniques for anthropomorphic limbs. In Graphical Models 62 (5), 353–388. Google ScholarDigital Library
36. WITKIN, A., AND KASS, M. 1988. Spacetime constraints. In Computer Graphics (Proc. of SIGGRAPH 88), vol. 22, 159–168. Google ScholarDigital Library
37. YAMANE, K., AND NAKAMURA, Y. 2000. Dynamics filter — concept and implementation of on-line motion generator for human figures. In Proc. IEEE Intl. Conference on Robotics and Automation, 688–695.Google Scholar