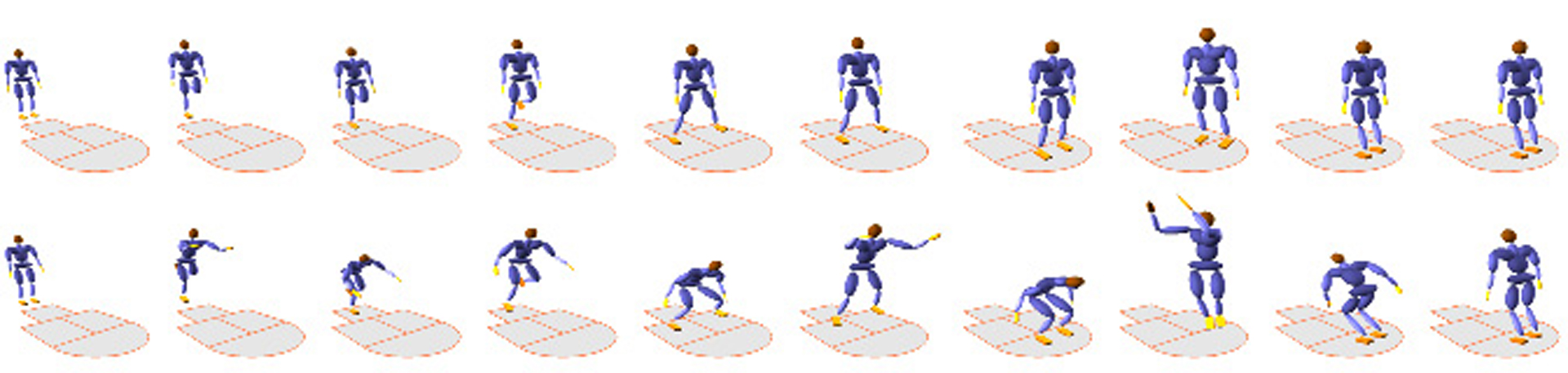
“Synthesis of complex dynamic character motion from simple animations”

In this paper we present a general method for rapid prototyping of realistic character motion. We solve for the natural motion from a simple animation provided by the animator. Our framework can be used to produce relatively complex realistic motion with little user effort.We describe a novel constraint detection method that automatically determines different constraints on the character by analyzing the input motion. We show that realistic motion can be achieved by enforcing a small set of linear and angular momentum constraints. This simplified approach helps us avoid the complexities of computing muscle forces. Simpler dynamic constraints also allow us to generate animations of models with greater complexity, performing more intricate motions. Finally, we show that by learning a small set of key parameters that describe a character pose we can help a non-skilled animator rapidly create realistic character motion.

1. ALEXANDER, R. M. 1980. Optimum walking techniques for quadrupeds and bipeds. J. Zool., London 192, 97-117.Google Scholar
2. ALEXANDER, R. M. 1989. Optimization and gaits in the locomotion of vertebrates. Physiol. Rev. 69, 1199-1227.Google Scholar
3. ALEXANDER, R. M. 1990. Optimum take-off techniques for high and long jumps. Phil. Trans. R. Soc. Lond. 329, 3-10.Google Scholar
4. ALEXANDER, R. M. 1991. Optimum timing of muscle activation for simple models of throwing. J. Theor. Biol. 150, 349-372.Google Scholar
5. BLICKHAN, R., AND FULL, R. J. 1993. Similarity in multilegged locomotion: bouncing like a monopode. J Comp. Physiol. A. 173, 509-517.Google Scholar
6. BLICKHAN, A. S. A. F. V. W. R. 1999. Dynamics of the long jump. Jornal of Biomechanics 32, 1259-1267.Google Scholar
7. BRUDERLIN, A., AND CALVERT, T. W. 1989. Goal-directed, dynamic animation of human walking. Computer Graphics 23, 3 (July), 233-242. Google Scholar
8. BRUDERLIN, A., AND WILLIAMS, L. 1995. Motion signal processing. In Computer Graphics (SIGGRAPH 95 Proceedings), 97-104. Google Scholar
9. COHEN, M. F. 1992. Interactive spacetime control for animation. In Computer Graphics (SIGGRAPH 92 Proceedings), vol. 26, 293-302. Google Scholar
10. DE LEVA, P. 1996. Adjustments to Zatsiorsky-Seluyanov’s segment inertia parameters. J. of Biomechanics 29, 9, 1223-1230.Google Scholar
11. DISCREET. Character studio. http://www.discreet.com/products/cs/.Google Scholar
12. FALOUTSOS, P., VAN DE PANNE, M., AND TERZOPOULOS, D. 2001. Composable controllers for physics-based character animation. In Proceedings of SIGGRAPH 2001, ACM Press / ACM SIGGRAPH, Computer Graphics Proceedings, Annual Conference Series, 251-260. ISBN 1-58113-292-1. Google Scholar
13. GILL, P., SAUNDERS, M., AND MURRAY, W. 1996. SNOPT: An SQP algorithm for large-scale constrained optimization. Tech. Rep. NA 96-2, University of California, San Diego.Google Scholar
14. GLEICHER, M., AND LITWINOWICZ, P. 1998. Constraint-based motion adaptation. The Journal of Visualization and Computer Animation 9, 2, 65-94.Google Scholar
15. GLEICHER, M. 1997. Motion editing with spacetime constraints. In 1997 Symposium on Interactive 3D Graphics, M. Cohen and D. Zeltzer, Eds., ACM SIGGRAPH, 139-148. ISBN 0-89791-884-3. Google Scholar
16. GLEICHER, M. 1998. Retargeting motion to new characters. In Computer Graphics (SIGGRAPH 98 Proceedings), 33-42. Google Scholar
17. GLEICHER, M. 2001. Motion path editing. In 2001 ACM Symposium on Interactive 3D Graphics, 195-202. ISBN 1-58113-292-1. Google Scholar
18. HODGINS, J. K., AND POLLARD, N. S. August 1997. Adapting simulated behaviors for new characters. Proceedings of SIGGRAPH 97, 153-162. ISBN 0-89791-896-7. Held in Los Angeles, California. Google Scholar
19. HODGINS, J. K., WOOTEN, W. L., BROGAN, D. C., AND O’BRIEN, J. F. 1995. Animating human athletics. Proceedings of SIGGRAPH 95 (August), 71-78. ISBN 0-201-84776-0. Held in Los Angeles, California. Google Scholar
20. HODGINS, J. K. 1998. Animating human motion. Scientific American 278, 3 (Mar.), 64-69.Google Scholar
21. HULL, M. P. F. C. A. D. G. 1991. A parameter optimization approach for the optimal control of large-scale musculoskeletal systems. Journal of Biomechanical Engineering 114, 450-460.Google Scholar
22. IGARASHI, T., MATSUOKA, S., AND TANAKA, H. 1999. Teddy: A sketching interface for 3d freeform design. Proceedings of SIGGRAPH 99 (August), 409-416. ISBN 0-20148-560-5. Held in Los Angeles, California. Google Scholar
23. KING, D. 1999. Generating vertical velocity and angular momentum during skating jumps. 23rd Annual Meeting of the American Society of Biomechanics (Oct).Google Scholar
24. LASZLO, J., VAN DE PANNE, M., AND FIUME, E. L. 2000. Interactive control for physically-based animation. Proceedings of SIGGRAPH 2000 (July), 201-208. ISBN 1-58113-208-5. Google Scholar
25. LEE, J., AND SHIN, S. Y. 1999. A hierarchical approach to interactive motion editing for human-like figures. In Computer Graphics (SIGGRAPH 99 Proceedings). Google Scholar
26. LIU, Z., GORTLER, S. J., AND COHEN, M. F. 1994. Hierarchical spacetime control. In Computer Graphics (SIGGRAPH 94 Proceedings). Google Scholar
27. PANDY, M., AND ZAJAC, F. E. 1991. Optimum timing of muscle activation for simple models of throwing. J. Biomechanics 24, 1-10.Google Scholar
28. PANDY, M., ZAJAC, F. E., SIM, E., AND LEVINE, W. S. 1990. An optimal control model of maximum-height human jumping. J. Biomechanics 23, 1185-1198.Google Scholar
29. PANDY, M., ANDERSON, F. C., AND HULL, D. G. 1992. A parameter optimization approach for the optimal control of large-scale musculoskeletal systems. J. of Biomech. Eng. (Nov.), 450-460.Google Scholar
30. PEARSALL, D., REID, J., AND ROSS, R. 1994. Inertial properties of the human trunk of males determined from magnetic resonance imaging. Annals of Biomed. Eng. 22, 692-706.Google Scholar
31. POLLARD, N. S., AND BEHMARAM-MOSAVAT, F. 2000. Force-based motion editing for locomotion tasks. In Proceedings of the IEEE International Conference on Robotics and Automation.Google Scholar
32. POLLARD, N. S., AND REITSMA, P. S. A. 2001. Animation of humanlike characters: Dynamic motion filtering with a physically plausible contact model. In Yale Workshop on Adaptive and Learning Systems.Google Scholar
33. POLLARD, N. S. 1999. Simple machines for scaling human motion. In Computer Animation and Simulation ’99, Eurographics, Milano, Italy. ISBN 3-211-83392-7.Google Scholar
34. POPOVIĆ, Z., AND WITKIN, A. 1999. Physically based motion transformation. In Computer Graphics (SIGRAPH 99 Proceedings). Google Scholar
35. POPOVIĆ, J., SEITZ, S. M., ERDMANN, M., POPOVIĆ, Z., AND WITKIN, A. P. 2000. Interactive manipulation of rigid body simulations. Proceedings of SIGGRAPH 2000 (July), 209-218. ISBN 1-58113-208-5. Google Scholar
36. RAIBERT, M. H., AND HODGINS, J. K. 1991. Animation of dynamic legged locomotion. In Computer Graphics (SIGGRAPH 91 Proceedings), vol. 25, 349-358. Google Scholar
37. ROSE, C., GUENTER, B., BODENHEIMER, B., AND COHEN, M. 1996. Efficient generation of motion transitions using spacetime constraints. In Computer Graphics (SIGGRAPH 96 Proceedings), 147-154. Google Scholar
38. ROSE, C., COHEN, M. F., AND BODENHEIMER, B. 1998. Verbs and adverbs: Multidimensional motion interpolation. IEEE Computer Graphics & Applications 18, 5 (Sept. – Oct.). Google Scholar
39. SHIN, H. J., LEE, J., GLEICHER, M., AND SHIN, S. Y. 2001. Computer puppetry: An impotance-based approach. ACM Transactions on Graphics 20, 2 (April), 67-94. ISSN 0730-0301. Google Scholar
40. TAK, S., SONG, O.-Y., AND KO, H.-S. 2000. Motion balance filtering. In Proceedings of the 21th European Conference on Computer Graphics (Eurographics-00), Blackwell Publishers, Cambridge, S. Coquillart and J. Duke, David, Eds., vol. 19, 3 of Computer Graphics Forum, 437-446.Google Scholar
41. TORKOS, N., AND VAN DE PANNE, M. 1998. Footprint-based quadruped motion synthesis. In Graphics Interface ’98, 151-160. ISBN 0-9695338-6-1.Google Scholar
42. VAN DE PANNE, M., AND FIUME, E. 1993. Sensor-actuator networks. In Computer Graphics (SIGGRAPH 93 Proceedings), vol. 27, 335-342. Google Scholar
43. VAN DE PANNE, M., AND FIUME, E. 1994. Virtual wind-up toys. In Proceedings of Graphics Interface 94.Google Scholar
44. VAN DE PANNE, M., KIM, R., AND FIUME, E. 1994. Virtual wind-up toys for animation. Graphics Interface ’94 (May), 208-215. Held in Banff, Alberta, Canada.Google Scholar
45. VAN DE PANNE, M. 1997. From footprints to animation. Computer Graphics Forum 16, 4, 211-224.Google Scholar
46. WITKIN, A., AND KASS, M. 1988. Spacetime constraints. In Computer Graphics (SIGGRAPH 88 Proceedings), vol. 22, 159-168. Google Scholar
47. WITKIN, A., AND POPOVIĆ, Z. 1995. Motion warping. In Computer Graphics (SIGGRAPH 95 Proceedings). Google Scholar
48. WOOTEN, W. L. 1998. Simulation of leaping, tumbling, landing, and balancing humans. PhD thesis, Georgia Institute of Technology. Google Scholar
49. YEADON, M. R. 1990. The simulation of aerial momement – iii the determination of the angular momentum of the human body. Journal of Biomechanics 23, 75-83.Google Scholar
50. ZORDAN, V. B., AND HODGINS, J. K. 1999. Tracking and modifying upper-body human motion data with dynamic simulation. In Computer Animation and Simulation ’99, Eurographics, Milano, Italy. ISBN 3-211-83392-7. Google Scholar