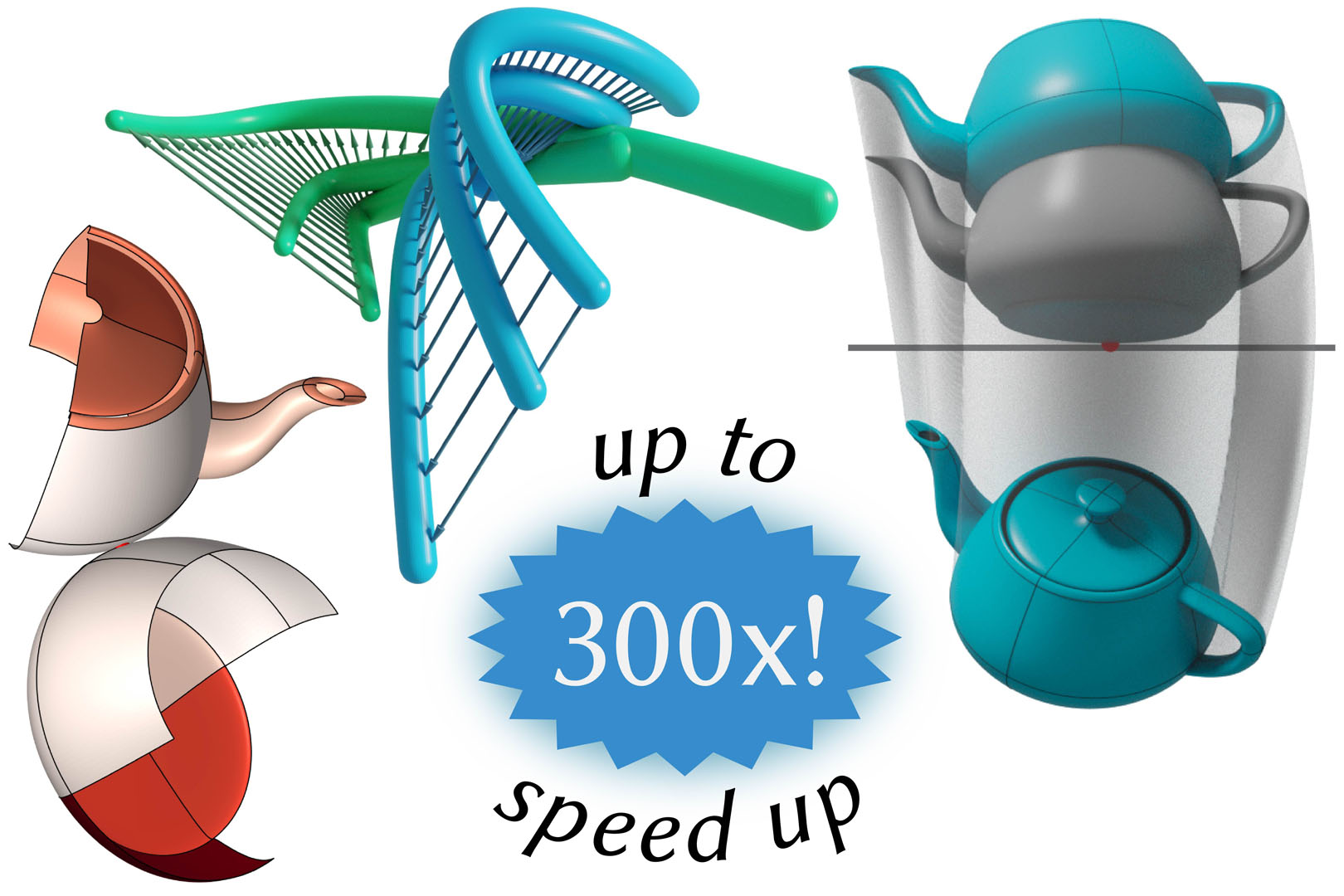
“Sum-of-Squares Collision Detection for Curved Shapes and Paths” by Zhang, Marschner, Solomon and Tamstorf
Conference:
Type(s):
Title:
- Sum-of-Squares Collision Detection for Curved Shapes and Paths
Session/Category Title: Making Contact: Simulating and Detecting Collisions
Presenter(s)/Author(s):
Moderator(s):
Abstract:
Sum-of-Squares Programming (SOSP) has recently been introduced to graphics as a unified way to address a large set of difficult problems involving higher order primitives. Unfortunately, a challenging aspect of this approach is the computational cost—especially for problems involving multiple geometries like collision detection. In this paper, we present techniques to reduce the cost of SOSP significantly. We use these improvements to speed up difficult problems like collision detection between Bézier triangles by as much as 300 ×. In addition, motivated by hair bundle simulation, we present SOSP based collision detection on the tapered cubic cylinder. We also present an algebraic formulation of rigid body motion enabling SOSP based collision detection for curved geometries and trajectories simultaneously. While these new formulations are complex, our speedups make them feasible. These advances improve the applicability of SOSP based collision detection and enable the continued progress of higher-order geometry processing.
References:
1. Amir Ahmadi, Georgina Hall, Ameesh Makadia, and Vikas Sindhwani. 2017. Geometry of 3D Environments and Sum of Squares Polynomials. In Robotics: Science and Systems XIII (Cambridge, Massachusetts), Nora Ayanian Nancy Amato, Siddhartha Srinivasa and Scott Kuindersma (Eds.). 9 pages. https://doi.org/10.15607/RSS.2017.XIII.071
2. Farid Alizadeh. 1995. Interior point methods in semidefinite programming with applications to combinatorial optimization. SIAM Journal on Optimization 5, 1 (1995), 13–51. https://doi.org/10.1137/0805002
3. Alexandre Amice, Hongkai Dai, Peter Werner, Annan Zhang, and Russ Tedrake. 2023. Finding and Optimizing Certified, Collision-Free Regions in Configuration Space for Robot Manipulators. In Algorithmic Foundations of Robotics XV. WAFR 2022(Springer Proceedings in Advanced Robotics, Vol. 25). Springer, Cham, 328–348. https://doi.org/10.1007/978-3-031-21090-7_20
4. Miklós Bergou, Basile Audoly, Etienne Vouga, Max Wardetzky, and Eitan Grinspun. 2010. Discrete Viscous Threads. ACM Transactions on Graphics 29, 4, Article 116 (jul 2010), 10 pages. https://doi.org/10.1145/1778765.1778853
5. Florence Bertails, Basile Audoly, Marie-Paule Cani, Bernard Querleux, Frédéric Leroy, and Jean-Luc Lévêque. 2006. Super-helices for predicting the dynamics of natural hair. ACM Transactions on Graphics (TOG) 25, 3 (2006), 1180–1187.
6. Grigoriy Blekherman, Pablo A. Parrilo, and Rekha R. Thomas. 2012. Semidefinite Optimization and Convex Algebraic Geometry. Society for Industrial and Applied Mathematics, Philadelphia, PA. https://doi.org/10.1137/1.9781611972290
7. Brent Burley, David Adler, Matt Jen-Yuan Chiang, Hank Driskill, Ralf Habel, Patrick Kelly, Peter Kutz, Yining Karl Li, and Daniel Teece. 2018. The Design and Evolution of Disney’s Hyperion Renderer. ACM Transactions on Graphics 37, 3, Article 33 (jul 2018), 22 pages. https://doi.org/10.1145/3182159
8. Konstantinos Daniilidis. 1999. Hand-Eye Calibration Using Dual Quaternions. The International Journal of Robotics Research 18, 3 (1999), 286–298. https://doi.org/10.1177/02783649922066213
9. Laura De Lorenzis, Peter Wriggers, and Thomas J.R. Hughes. 2014. Isogeometric contact: a review. GAMM-Mitteilungen 37, 1 (2014), 85–123. https://doi.org/10.1002/gamm.201410005
10. Zachary Ferguson, Pranav Jain, Denis Zorin, Teseo Schneider, and Daniele Panozzo. 2022. High-Order Incremental Potential Contact for Elastodynamic Simulation on Curved Meshes. arxiv:2205.13727 [cs.GR]
11. Zachary Ferguson, Minchen Li, Teseo Schneider, Francisca Gil-Ureta, Timothy Langlois, Chenfanfu Jiang, Denis Zorin, Danny M. Kaufman, and Daniele Panozzo. 2021. Intersection-Free Rigid Body Dynamics. ACM Transactions on Graphics 40, 4, Article 183 (jul 2021), 16 pages. https://doi.org/10.1145/3450626.3459802
12. Thomas J. R. Hughes, John Austin Cottrell, and Yuri Bazilevs. 2005. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Computer Methods in Applied Mechanics and Engineering 194, 39 (2005), 4135 – 4195. https://doi.org/10.1016/j.cma.2004.10.008
13. Yan-Bin Jia. 2013. Dual quaternions. Iowa State University: Ames, IA, USA. https://faculty.sites.iastate.edu/jia/files/inline-files/dual-quaternion.pdf
14. Ladislav Kavan, Steven Collins, Carol O’Sullivan, and Jiří Žára. 2006. Dual quaternions for rigid transformation blending. Technical Report TCD-CS-2006–46. Trinity College Dublin.
15. Ladislav Kavan, Steven Collins, Jiří Žára, and Carol O’Sullivan. 2008. Geometric Skinning with Approximate Dual Quaternion Blending. ACM Transactions on Graphics 27, 4, Article 105 (nov 2008), 23 pages. https://doi.org/10.1145/1409625.1409627
16. Christopher Kulla, Alejandro Conty, Clifford Stein, and Larry Gritz. 2018. Sony Pictures Imageworks Arnold. ACM Transactions on Graphics 37, 3, Article 29 (aug 2018), 18 pages. https://doi.org/10.1145/3180495
17. Monique Laurent. 2007. Semidefinite representations for finite varieties. Mathematical programming 109, 1 (2007), 1–26. https://doi.org/10.1007/s10107-004-0561-4
18. Johan Löfberg. 2004. YALMIP: A Toolbox for Modeling and Optimization in MATLAB. In IEEE International Symposium on Computer Aided Control System Design (CACSD) (Taipei, Taiwan). IEEE, Piscataway, NJ, 284–289. https://doi.org/10.1109/CACSD.2004.1393890
19. Jia Lu and Chao Zheng. 2014. Dynamic cloth simulation by isogeometric analysis. Computer Methods in Applied Mechanics and Engineering 268 (2014), 475–493. https://doi.org/10.1016/j.cma.2013.09.016
20. Zoë Marschner, David Palmer, Paul Zhang, and Justin Solomon. 2020. Hexahedral Mesh Repair via Sum-of-Squares Relaxation. Computer Graphics Forum 39, 5 (2020), 133–147. https://doi.org/10.1111/cgf.14074
21. Zoë Marschner, Paul Zhang, David Palmer, and Justin Solomon. 2021. Sum-of-Squares Geometry Processing. ACM Transactions on Graphics 40, 6, Article 253 (dec 2021), 13 pages. https://doi.org/10.1145/3478513.3480551
22. MOSEK ApS. 2020. The MOSEK optimization toolbox for MATLAB manual. Version 8.1.0.83. https://docs.mosek.com/8.1/toolbox.pdf
23. Koji Nakamaru and Yoshio Ohno. 2002. Ray tracing for curves primitive. Journal of WSCG 10, 1-2 (2002), 6 pages. http://wscg.zcu.cz/wscg2002/Papers_2002/A83.pdf
24. Yurii Nesterov and Arkadii Nemirovskii. 1994. Interior-Point Polynomial Algorithms in Convex Programming. Society for Industrial and Applied Mathematics, Philadelphia, PA. https://doi.org/10.1137/1.9781611970791
25. Jiawang Nie. 2014. Optimality conditions and finite convergence of Lasserre’s hierarchy. Mathematical programming 146, 1 (2014), 97–121. https://doi.org/10.1007/s10107-013-0680-x
26. Pablo A. Parrilo. 2000. Structured semidefinite programs and semialgebraic geometry methods in robustness and optimization. Ph. D. Dissertation. California Institute of Technology. https://doi.org/10.7907/2K6Y-CH43
27. Pablo A. Parrilo. 2019. Algebraic Techniques and Semidefinite Optimization. https://learning-modules.mit.edu/materials/index.html?uuid=/course/6/sp19/6.256#materials.
28. George Vikram Paul. 1997. Kinematics of Objects in Contact using Dual Vectors and its Applications. Ph. D. Dissertation. Carnegie Mellon University. https://www.ri.cmu.edu/pub_files/pub3/paul_george_1997_1/paul_george_1997_1.pdf
29. Xavier Provot. 1997. Collision and self-collision handling in cloth model dedicated to design garments. In Computer Animation and Simulation’97: Proceedings of the Eurographics Workshop in Budapest, Hungary, September 2–3, 1997. Springer, 177–189.
30. Mihai Putinar. 1993. Positive polynomials on compact semi-algebraic sets. Indiana University Mathematics Journal 42, 3 (1993), 969–984. https://www.jstor.org/stable/24897130
31. Stephane Redon, Abderrahmane Kheddar, and Sabine Coquillart. 2000. An algebraic solution to the problem of collision detection for rigid polyhedral objects. In Proceedings of the IEEE International Conference on Robotics and Automation, Vol. 4. IEEE, Piscataway, NJ, 3733–3738. https://doi.org/10.1109/ROBOT.2000.845313
32. Teseo Schneider, Yixin Hu, Xifeng Gao, Jérémie Dumas, Denis Zorin, and Daniele Panozzo. 2022. A Large-Scale Comparison of Tetrahedral and Hexahedral Elements for Solving Elliptic PDEs with the Finite Element Method. ACM Transactions on Graphics 41, 3, Article 23 (mar 2022), 14 pages. https://doi.org/10.1145/3508372
33. Jonathan Mark Selig. 2005. Geometric Fundamentals of Robotics (2nd ed.). Springer, New York, NY. https://doi.org/10.1007/b138859
34. John M. Snyder. 1992. Interval Analysis for Computer Graphics. In Proceedings of the 19th Annual Conference on Computer Graphics and Interactive Techniques(SIGGRAPH ’92). Association for Computing Machinery, New York, NY, USA, 121–130. https://doi.org/10.1145/142920.134024
35. John M. Snyder, Adam R. Woodbury, Kurt Fleischer, Bena Currin, and Alan H. Barr. 1993. Interval Methods for Multi-Point Collisions between Time-Dependent Curved Surfaces. In Proceedings of the 20th Annual Conference on Computer Graphics and Interactive Techniques(SIGGRAPH ’93). Association for Computing Machinery, New York, NY, USA, 321–334. https://doi.org/10.1145/166117.166158
36. Marc Thyng, Christopher Evart, Toby Jones, and Aleka McAdams. 2017. The Art and Technology of Hair Simulation in Disney’s Moana. In ACM SIGGRAPH 2017 Talks (Los Angeles, California) (SIGGRAPH ’17). Association for Computing Machinery, New York, NY, USA, Article 25, 2 pages. https://doi.org/10.1145/3084363.3085072
37. Ty Trusty, Honglin Chen, and David I. W. Levin. 2021. The Shape Matching Element Method: Direct Animation of Curved Surface Models. ACM Transactions on Graphics 40, 4, Article 69 (jul 2021), 14 pages. https://doi.org/10.1145/3450626.3459772
38. Charles W. Wampler and Andrew J. Sommese. 2011. Numerical algebraic geometry and algebraic kinematics. Acta Numerica 20 (2011), 469–567. https://doi.org/10.1017/S0962492911000067
39. Bolun Wang, Zachary Ferguson, Teseo Schneider, Xin Jiang, Marco Attene, and Daniele Panozzo. 2021. A Large-Scale Benchmark and an Inclusion-Based Algorithm for Continuous Collision Detection. ACM Transactions on Graphics 40, 5, Article 188 (sep 2021), 16 pages. https://doi.org/10.1145/3460775
40. Heng Yang, Ling Liang, Luca Carlone, and Kim-Chuan Toh. 2022. An inexact projected gradient method with rounding and lifting by nonlinear programming for solving rank-one semidefinite relaxation of polynomial optimization. Mathematical Programming (2022), 1–64. https://doi.org/10.1007/s10107-022-01912-6
41. Chris Yu, Caleb Brakensiek, Henrik Schumacher, and Keenan Crane. 2021. Repulsive Surfaces. ACM Transactions on Graphics 40, 6, Article 268 (dec 2021), 19 pages. https://doi.org/10.1145/3478513.3480521