“Stress relief: improving structural strength of 3D printable objects” by Stava, Vanek, Benes, Carr and Mech

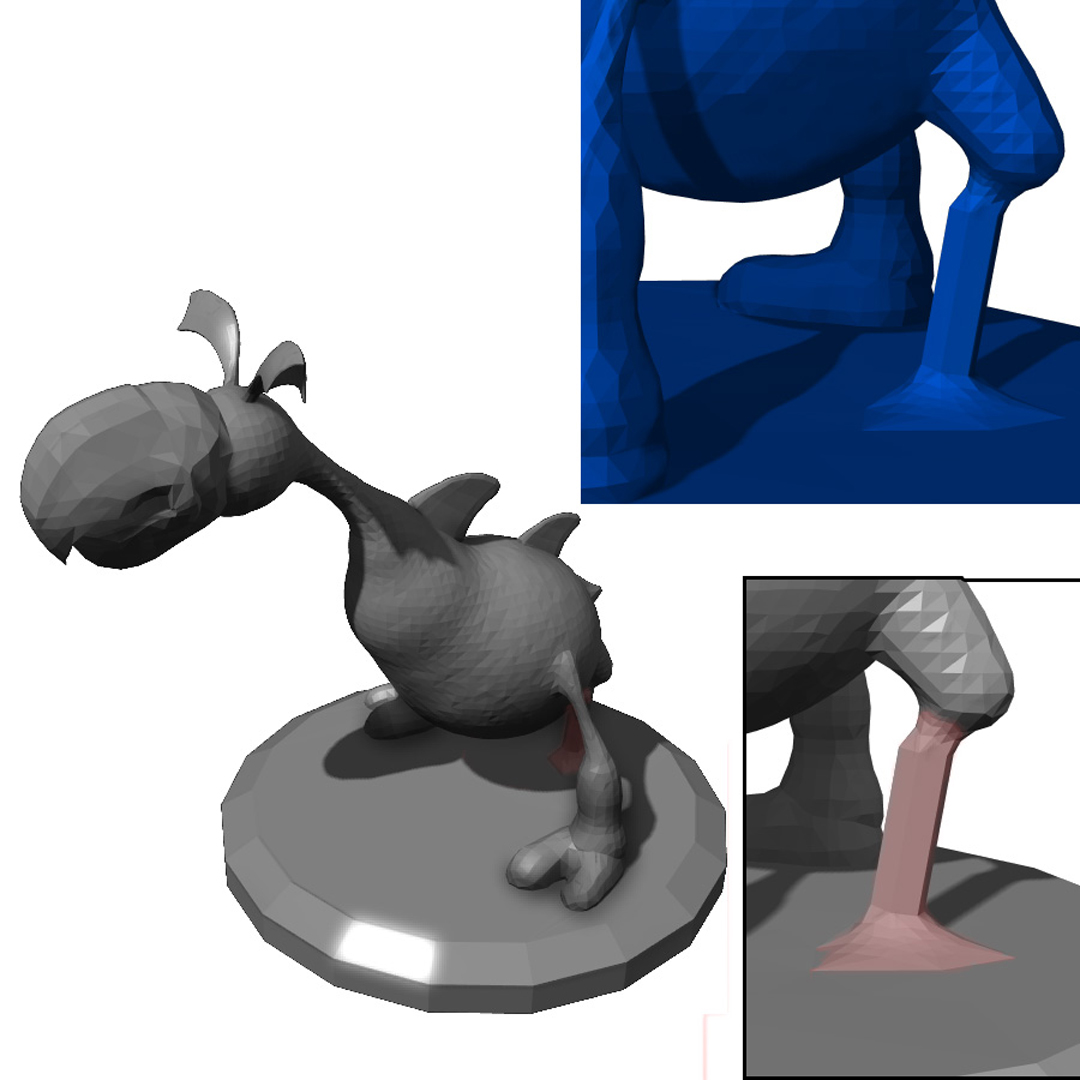
The use of 3D printing has rapidly expanded in the past couple of years. It is now possible to produce 3D-printed objects with exceptionally high fidelity and precision. However, although the quality of 3D printing has improved, both the time to print and the material costs have remained high. Moreover, there is no guarantee that a printed model is structurally sound. The printed product often does not survive cleaning, transportation, or handling, or it may even collapse under its own weight. We present a system that addresses this issue by providing automatic detection and correction of the problematic cases. The structural problems are detected by combining a lightweight structural analysis solver with 3D medial axis approximations. After areas with high structural stress are found, the model is corrected by combining three approaches: hollowing, thickening, and strut insertion. Both detection and correction steps are repeated until the problems have been eliminated. Our process is designed to create a model that is visually similar to the original model but possessing greater structural integrity.

1. Allaire, G., and Jouve, F. 2008. Minimum stress optimal design with the level set method. Engineering Analysis with Boundary Elements 32, 11, 909–918.Google ScholarCross Ref
2. Allaire. 2002. A level-set method for shape optimization. Comptes Rendus Mathematique 334, 12, 1125–1130.Google ScholarCross Ref
3. Allaire, G. 2004. Structural optimization using sensitivity analysis and a level-set method. Journal of Computational Physics 194, 1, 363–393. Google ScholarDigital Library
4. Andrews, J., Joshi, P., and Carr, N. 2011. A linear variational system for modelling from curves. Comput. Graph. Forum.Google Scholar
5. Balasubramanian, R., Xu, L., Brook, P. D., Smith, J. R., and Matsuoka, Y. 2010. Human-guided grasp measures improve grasp robustness on physical robot. In ICRA, 2294–2301.Google Scholar
6. Butcher, J. C. 2008. Numerical Methods for Ordinary Differential Equations. John Wiley and Sons, Ltd.Google Scholar
7. Cohen, J., Varshney, A., Manocha, D., Turk, G., Weber, H., Agarwal, P., Brooks, F., and Wright, W. 1996. Simplification envelopes. In Proceedings of the 23rd annual conference on Computer graphics and interactive techniques, ACM, New York, NY, USA, SIGGRAPH ’96, 119–128. Google ScholarDigital Library
8. Dey, T. K., and Zhao, W. 2003. Approximating the medial axis from the voronoi diagram with a convergence guarantee. Algorithmica 38 (October), 179–200. Google ScholarDigital Library
9. Engineering Handbook, 2011. Rapid Prototyping — Processes. http://engineershandbook.com/RapidPrototyping/rpprocesses.htm.Google Scholar
10. Fu, H., Cohen-Or, D., Dror, G., and Sheffer, A. 2008. Upright orientation of man-made objects. ACM Trans. Graph. 27 (August), 42:1–42:7. Google ScholarDigital Library
11. Golub, G. H., and Welsch, J. H. 1967. Calculation of gauss quadrature rules. Tech. rep., Stanford, CA, USA. Google ScholarDigital Library
12. Hart, J. C., Baker, B., and Michaelraj, J. 2003. Structural simulation of tree growth and response. The Visual Computer 19, 2–3, 151–163.Google ScholarCross Ref
13. Haslinger, J., AND Mäkinen, R. A. E. 2003. Introduction to Shape Optimization: Theory, Approximation, and Computation. SIAM, Philadelphia. Google ScholarDigital Library
14. Hornung, A., and Kobbelt, L. 2006. Robust reconstruction of watertight 3d models from non-uniformly sampled point clouds without normal information. In Proc. of Symposium on Geometry Processing, Eurographics Association, 41–50. Google ScholarDigital Library
15. Hughes, T. J. R. 1987. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis. Prentice-Hall.Google Scholar
16. Jirasek, C., Prusinkiewicz, P., and Moulia, B. 2000. Integrating biomechanics into developmental plant models expressed using 1-systems. In Proc. Plant Biomechanics, 615–624.Google Scholar
17. Kinoshita, H., Bäckström, L., Flanagan, J. R., and Johansson, R. S. 1997. Tangential torque effects on the control of grip forces when holding objects with a precision grip. Journal of Neurophysiology 78, 3, 1619–1630.Google ScholarCross Ref
18. Liu, R., Burschka, D., and Hirzinger, G. 2007. On the way to water-tight mesh. In Proc. of ISPRS.Google Scholar
19. Liu, L., Chambers, E. W., Letscher, D., and Ju, T. 2010. A simple and robust thinning algorithm on cell complexes. Comput. Graph. Forum 29, 7, 2253–2260.Google ScholarCross Ref
20. Osher, S., and Sethian, J. A. 1988. Fronts propagating with curvature dependent speed. Journal of Computational Physics 79, 12–49. Google ScholarDigital Library
21. Peng, J., Kristjansson, D., and Zorin, D. 2004. Interactive modeling of topologically complex geometric detail. In ACM SIGGRAPH 2004 Papers, ACM, New York, NY, USA, SIGGRAPH ’04, 635–643. Google ScholarDigital Library
22. Schmidt, R., and Singh, K. 2010. meshmixer: an interface for rapid mesh composition. In ACM SIGGRAPH 2010 Talks, SIGGRAPH ’10, ACM, 6:1–6:1. Google ScholarDigital Library
23. Shapeways, 2011. 3D printing in 4 simple steps. http://www.shapeways.com/about/how_does_it_work.Google Scholar
24. Shapeways, 2011. Things to keep in mind when designing for 3D printing. http://www.shapeways.com/tutorials/things-to-keep-in-mind.Google Scholar
25. Shewchuk, J. R. 2001. Delaunay refinement algorithms for triangular mesh generation. Computational Geometry: Theory and Applications 22, 1–3. Google ScholarDigital Library
26. Si, H., 2011. Tetgen: A quality tetrahedral mesh generator and a 3D delaunay triangulator.Google Scholar
27. Telea, A., and Jalba, A. 2011. Voxel-based assessment of printability of 3d shapes. In Proc. of Mathematical morphology and its applications to image and signal processing, SpringerVerlag, Berlin, Heidelberg, ISMM, 393–404. Google ScholarDigital Library
28. von Mises, R. 1913. Mechanik der festen körper im plastisch-deformablen zustand. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse 1913, 582–592.Google Scholar
29. Whiting, E., Ochsendorf, J., and Durand, F. 2009. Procedural modeling of structurally-sound masonry buildings. ACM Trans. Graph. 28, 5, 112. Google ScholarDigital Library
30. Z Corporation, 2011. Architectural Design Guide – Printing 3D Architectural Models. http://crl.ap.buffalo.edu/digitalworkshop/zcorp/pdfs/archdesguide.pdf.Google Scholar