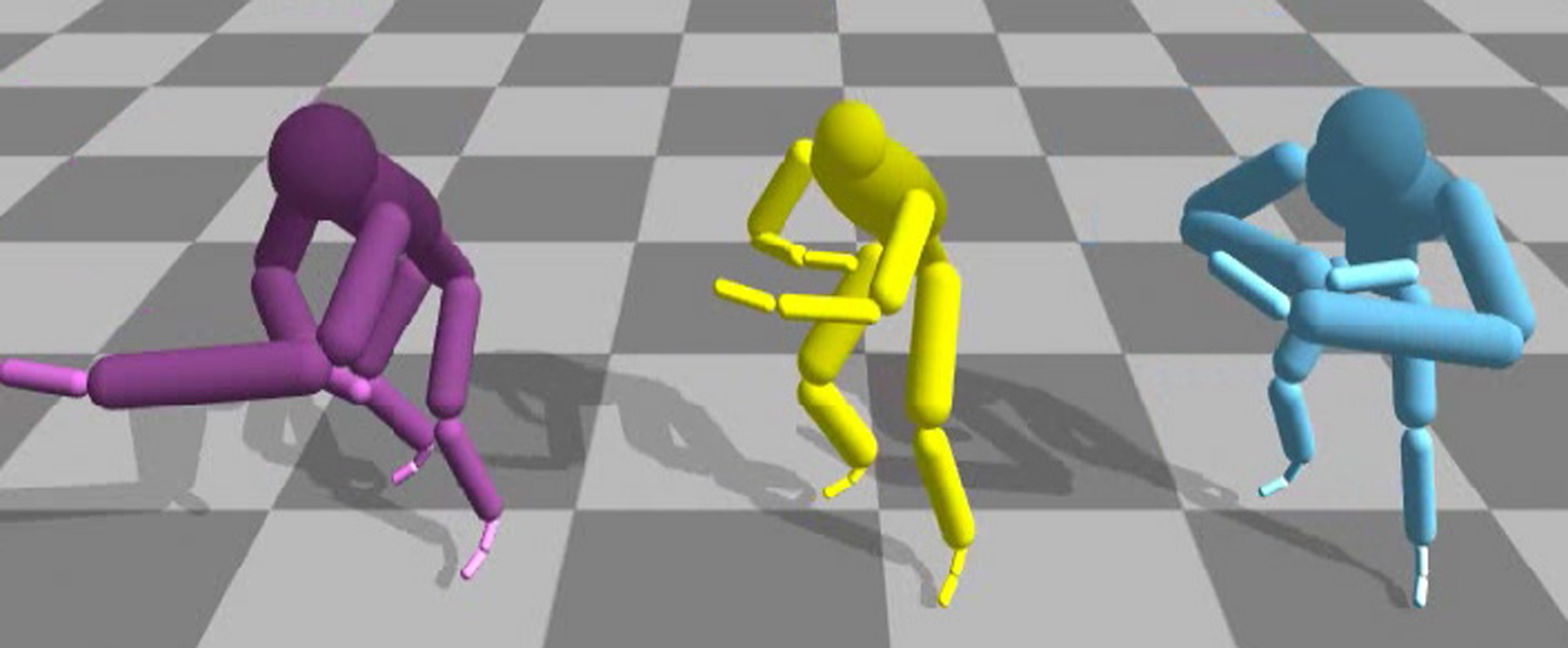
“Spatial relationship preserving character motion adaptation” by Ho, Komura and Tai
Conference:
Type(s):
Title:
- Spatial relationship preserving character motion adaptation
Presenter(s)/Author(s):
Abstract:
This paper presents a new method for editing and retargeting motions that involve close interactions between body parts of single or multiple articulated characters, such as dancing, wrestling, and sword fighting, or between characters and a restricted environment, such as getting into a car. In such motions, the implicit spatial relationships between body parts/objects are important for capturing the scene semantics. We introduce a simple structure called an interaction mesh to represent such spatial relationships. By minimizing the local deformation of the interaction meshes of animation frames, such relationships are preserved during motion editing while reducing the number of inappropriate interpenetrations. The interaction mesh representation is general and applicable to various kinds of close interactions. It also works well for interactions involving contacts and tangles as well as those without any contacts. The method is computationally efficient, allowing real-time character control. We demonstrate its effectiveness and versatility in synthesizing a wide variety of motions with close interactions.
References:
1. Alexa, M. 2003. Differential coordinates for local mesh morphing and deformation. The Visual Computer 19, 2–3, 105–114.Google ScholarCross Ref
2. Allen, B., Curless, B., and Popović, Z. 2003. The space of human body shapes: reconstruction and parameterization from range scans. ACM Transactions on Graphics 22, 3 (Jul.), 587–594. Google ScholarDigital Library
3. Badler, N. I., Palmer, M. S., and Bindiganavale, R. 1999. Animation control for real-time virtual humans. Communications of the ACM 42, 8, 64–73. Google ScholarDigital Library
4. Bodenheimer, B., Rose, C., Rosenthal, S., and Pella., J. 1997. The process of motion capture: Dealing with the data. In Computer Animation and Simulation 97, 318.Google Scholar
5. Bolz, J., Farmer, I., Grinspun, E., and Schröoder, P. 2003. Sparse matrix solvers on the gpu: conjugate gradients and multigrid. ACM Transactions on Graphics 22, 3 (Jul.), 917–924. Google ScholarDigital Library
6. Callennec, B. L., and Boulic, R. 2004. Interactive motion deformation with prioritized constraints. In Proceedings of ACM SIGGRAPH/Eurographics Symposium on Computer Animation, 163–171. Google ScholarDigital Library
7. Choi, K.-J., and Ko, H.-S. 2000. Online motion retargeting. Journal of Visualization and Computer and Animation 11, 5, 223–235.Google ScholarCross Ref
8. da Silva, M., Abe, Y., and Popović, J. 2008. Interactive simulation of stylized human locomotion. ACM Transactions on Graphics 27, 3 (Aug.), 82:1–10. Google ScholarDigital Library
9. Davis, T. A. 2004. Algorithm 832: Umfpack, an unsymmetric-pattern multifrontal method. ACM Transactions on Mathematical Software 30, 2 (Jun.), 196–199. Google ScholarDigital Library
10. Fang, A. C., and Pollard, N. S. 2003. Efficient synthesis of physically valid human motion. ACM Transactions on Graphics 22, 3 (Jul.), 417–426. Google ScholarDigital Library
11. Gleicher, M. 1997. Motion editing with spacetime constraints. In Proceedings of Symposium on Interactive 3D Graphics, 139–148. Google ScholarDigital Library
12. Gleicher, M. 1998. Retargetting motion to new characters. In Proceedings of SIGGRAPH 98, ACM Press/ACM SIGGRAPH, M. Cohen, Ed., Computer Graphics Proceedings, Annual Conference Series, ACM, 33–42. Google ScholarDigital Library
13. Goto, K., and Van De Geijn, R. 2008. High-performance implementation of the level-3 blas. ACM Transactions on Mathematical Software 35, 1 (Jul.), 1–14. Google ScholarDigital Library
14. Ho, E. S. L., and Komura, T. 2009. Character motion synthesis by topology coordinates. Computer Graphics Forum 28, 2, 299–308.Google ScholarCross Ref
15. Ho, E. S. L., and Komura, T. 2009. Indexing and retrieving motions of characters in close contact. IEEE Transactions on Visualization and Computer Graphics 15, 3 (May), 481–492. Google ScholarDigital Library
16. Komura, T., Shinagawa, Y., and Kunii, T. L. 2000. Creating and retargetting motion by the musculoskeletal human body model. The Visual Computer, 5, 254–270.Google ScholarCross Ref
17. Komura, T., Leung, H., and Kuffner, J. 2004. Animating reactive motions for biped locomotion. In Proceedings of ACM Virtual Reality Software and Technology, 32–40. Google ScholarDigital Library
18. Kwon, T., Lee, K. H., Lee, J., and Takahashi, S. 2008. Group motion editing. ACM Transactions on Graphics 27, 3 (Aug.), 80:1–8. Google ScholarDigital Library
19. LaValle, S., and Kuffner, J. 2001. Rapidly-exploring random trees: Progress and prospects. In Robotics: The Algorithmic Perspective. 4th Int’l Workshop on the Algorithmic Foundations of Robotics, 293–308.Google Scholar
20. Lee, J., and Shin, S. Y. 1999. A hierarchical approach to interactive motion editing for human-like figures. In Proceedings of SIGGRAPH 99, ACM Press/ACM SIGGRAPH, A. Rockwood, Ed., Computer Graphics Proceedings, Annual Conference Series, ACM, 39–48. Google ScholarDigital Library
21. Liu, C. K., and Popović’, Z. 2002. Synthesis of complex dynamic character motion from simple animations. ACM Transactions on Graphics 21, 3 (Jul.), 408–416. Google ScholarDigital Library
22. Liu, C. K., Hertzmann, A., and Popovic, Z. 2006. Composition of complex optimal multi-character motions. In Proceedings of ACM SIGGRAPH/Eurographics Symposium on Computer Animation, 215–222. Google ScholarDigital Library
23. Lyard, E., and Magnenat-Thalmann, N. 2008. Motion adaptation based on character shape. Computer Animation and Virtual Worlds 19, 3–4, 189–198. Google ScholarDigital Library
24. Macchietto, A., Zordan, V., and Shelton, C. R. 2009. Momentum control for balance. ACM Transactions on Graphics 28, 3 (Aug.), 80:1–8. Google ScholarDigital Library
25. Popović, Z., and Witkin, A. 1999. Physically based motion transformation. In Proceedings of SIGGRAPH 99, ACM Press/ACM SIGGRAPH, A. Rockwood, Ed., Computer Graphics Proceedings, Annual Conference Series, ACM, 11–20. Google ScholarDigital Library
26. Shapiro, A., Kallmann, M., and Faloutsos, P. 2007. Interactive motion correction and object manipulation. In Proceedings of ACM SIGGRAPH Symposium on Interactive 3D graphics and Games, 137–144. Google ScholarDigital Library
27. Shi, X., Zhou, K., Tong, Y., Desbrun, M., Bao, H., and Guo, B. 2007. Mesh puppetry: Cascading optimization of mesh deformation with inverse kinematics. ACM Transactions on Graphics 26, 3 (Jul.), 81:1–9 Google ScholarDigital Library
28. Shum, H. P. H., Komura, T., and Yadav, P. 2009. Angular momentum guided motion concatenation. Computer Animation and Virtual Worlds 20, 2–3, 385–394. Google ScholarDigital Library
29. Si, H., and Gaertner, K. 2005. Meshing piecewise linear complexes by constrained delaunay tetrahedralizations. In Proceedings of the 14th International Meshing Roundtable, 147–163.Google Scholar
30. Smith, R. 2005. Open dynamics engine. www.ode.org.Google Scholar
31. Sorkine, O., Lipman, Y., Cohen-Or, D., Alexa, M., Rössl, C., and Seidel, H.-P. 2004. Laplacian surface editing. In Proceedings of the Eurographics/ACM SIGGRAPH Symposium on Geometry Processing, 179–188. Google ScholarDigital Library
32. Sumner, R. W., and Popovic, J. 2004. Deformation transfer for triangle meshes. ACM Transactions on Graphics 23, 3 (Aug.), 397–403. Google ScholarDigital Library
33. Xu, W., Zhou, K., Yu, Y., Tan, Q., Peng, Q., and Guo, B. 2007. Gradient domain editing of deforming mesh sequences. ACM Transactions on Graphics, 26, 3 (Jul.), 84:1–10. Google ScholarDigital Library
34. Yamane, K., Kuffner, J., and Hodgins, J. 2004. Synthesizing animations of human manipulation tasks. ACM Transactions on Graphics 23, 3 (Aug.), 532–539. Google ScholarDigital Library
35. Zayer, R., Rössl, C., Karni, Z., and Seidel, H.-P. 2005. Harmonic guidance for surface deformation. Computer Graphics Forum 24, 3, 601–609.Google ScholarCross Ref
36. Zhou, K., Huang, J., Snyder, J., Liu, X., Bao, H., Guo, B., and Shum, H.-Y. 2005. Large mesh deformation using the volumetric graph laplacian. ACM Transactions on Graphics 24, 3 (Jul.), 496–503. Google ScholarDigital Library
37. Zhou, K., Xu, W., Tong, Y., and Desbrun, M. 2010. Deformation transfer to multi-component objects. Computer Graphics Forum 29, 2.Google ScholarCross Ref