“Skeleton extraction by mesh contraction” by Kin-Chung Au, Tai, Chu, Cohen-Or and Lee

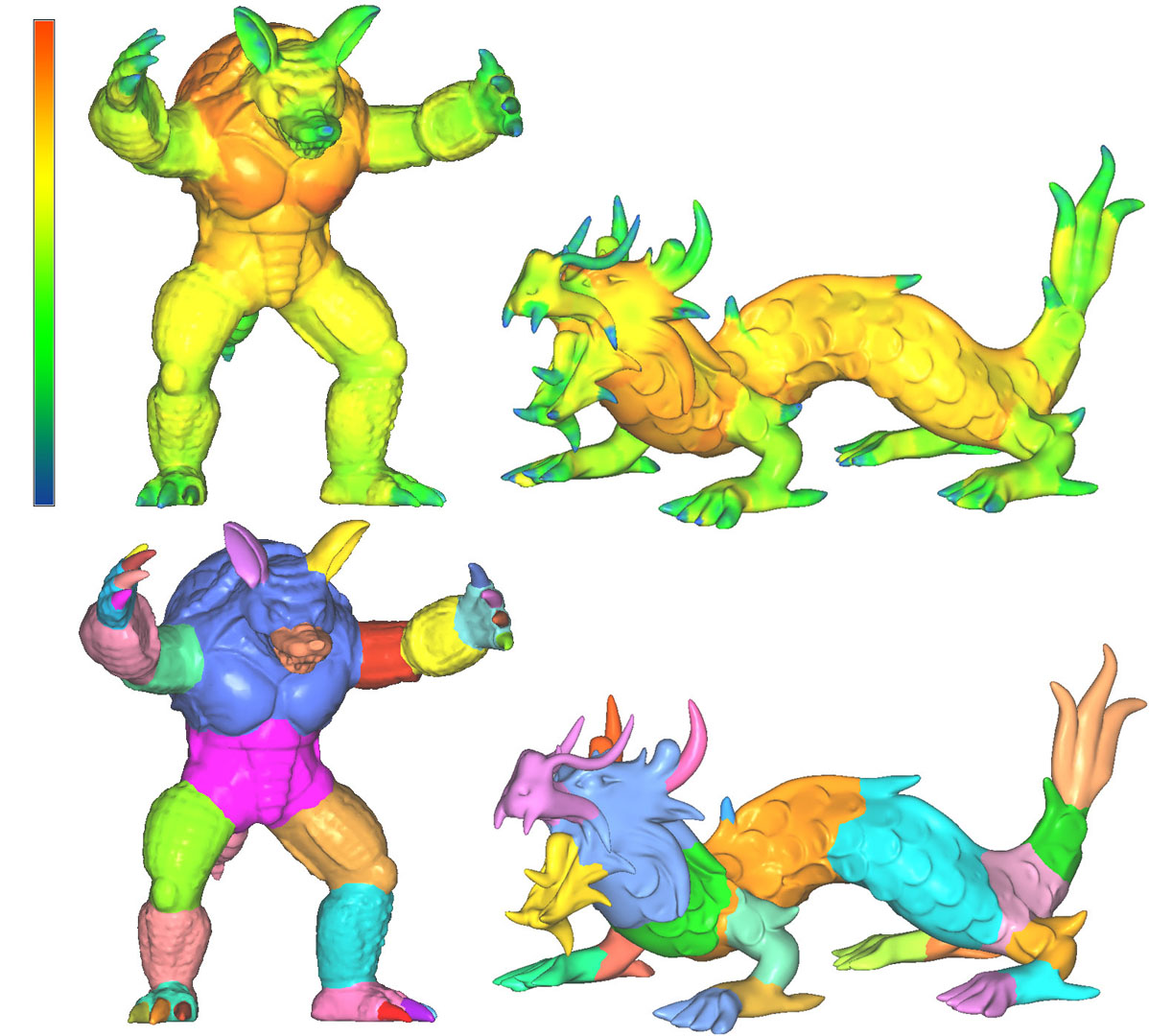
Extraction of curve-skeletons is a fundamental problem with many applications in computer graphics and visualization. In this paper, we present a simple and robust skeleton extraction method based on mesh contraction. The method works directly on the mesh domain, without pre-sampling the mesh model into a volumetric representation. The method first contracts the mesh geometry into zero-volume skeletal shape by applying implicit Laplacian smoothing with global positional constraints. The contraction does not alter the mesh connectivity and retains the key features of the original mesh. The contracted mesh is then converted into a 1D curve-skeleton through a connectivity surgery process to remove all the collapsed faces while preserving the shape of the contracted mesh and the original topology. The centeredness of the skeleton is refined by exploiting the induced skeleton-mesh mapping. In addition to producing a curve skeleton, the method generates other valuable information about the object’s geometry, in particular, the skeleton-vertex correspondence and the local thickness, which are useful for various applications. We demonstrate its effectiveness in mesh segmentation and skinning animation.

1. Amenta, N., Choi, S., and Kolluri, R. K. 2001. The power crust. In Symposium on Solid Modeling and Applications, 249–266. Google ScholarDigital Library
2. Aujay, G., Hétroy, F., Lazarus, F., and Depraz, C. 2007. Harmonic skeleton for realistic character animation. In Symposium on Computer Animation, 151–160. Google ScholarDigital Library
3. Baran, I., and Popović, J. 2007. Automatic rigging and animation of 3D characters. ACM Trans. Graph. 26, 3, Article 72. Google ScholarDigital Library
4. Bitter, I., Kaufman, A. E., and Sato, M. 2001. Penalized-distance volumetric skeleton algorithm. IEEE Transactions on Visualization and Computer Graphics 7, 3, 195–206. Google ScholarDigital Library
5. Chuang, J.-H., Tsai, C.-H., and Ko, M.-C. 2000. Skeletonization of three-dimensional object using generalized potential field. IEEE Trans. Pattern Anal. Mach. Intell. 22, 11, 1241–1251. Google ScholarDigital Library
6. Cornea, N. D., Silver, D., Yuan, X., and Balasubramanian, R. 2005. Computing hierarchical curve-skeletons of 3D objects. The Visual Computer 21, 11, 945–955.Google ScholarCross Ref
7. Cornea, N. D., Min, P., and Silver, D. 2007. Curve-skeleton properties, applications, and algorithms. IEEE Transactions on Visualization and Computer Graphics 13, 3, 530–548. Google ScholarDigital Library
8. Desbrun, M., Meyer, M., Schröder, P., and Barr, A. H. 1999. Implicit fairing of irregular meshes using diffusion and curvature flow. In Proceedings of ACM SIGGRAPH 99, 317–324. Google ScholarDigital Library
9. Dey, T. K., and Sun, J. 2006. Defining and computing curve-skeletons with medial geodesic function. In Symposium on Geometry Processing, 143–152. Google ScholarDigital Library
10. Garland, M., and Heckbert, P. S. 1997. Surface simplification using quadric error metrics. In Proceedings of ACM SIGGRAPH 97, 209–216. Google ScholarDigital Library
11. Hassouna, M. S., and Farag, A. A. 2005. Robust centerline extraction framework using level sets. In Proceedings on Computer Vision and Pattern Recognition – Volume 1, 458–465. Google ScholarDigital Library
12. Hilaga, M., Shinagawa, Y., Kohmura, T., and Kunii, T. L. 2001. Topology matching for fully automatic similarity estimation of 3D shapes. In ACM Trans. Graph., 203–212. Google ScholarDigital Library
13. Katz, S., and Tal, A. 2003. Hierarchical mesh decomposition using fuzzy clustering and cuts. In ACM Trans. Graph., 954–961. Google ScholarDigital Library
14. Katz, S., Leifman, G., and Tal, A. 2005. Mesh segmentation using feature point and core extraction. The Visual Computer 21, 8–10, 649–658.Google ScholarCross Ref
15. Li, X., Woon, T.-W., Tan, T.-S., and Huang, Z. 2001. Decomposing polygon meshes for interactive applications. In Symposium on Interactive 3D graphics, 35–42. Google ScholarDigital Library
16. Ma, C.-M., Wan, S.-Y., and Lee, J.-D. 2002. Three-dimensional topology preserving reduction on the 4-subfields. IEEE Trans. Pattern Anal. Mach. Intell. 24, 12, 1594–1605. Google ScholarDigital Library
17. Ma, W.-C., Wu, F.-C., and Ouhyoung, M. 2003. Skeleton extraction of 3D objects with radial basis functions. In Proceedings of the Shape Modeling International, 207–215. Google ScholarDigital Library
18. Nealen, A., Igarashi, T., Sorkine, O., and Alexa, M. 2006. Laplacian mesh optimization. In Proceedings of ACM GRAPHITE, 381–389. Google ScholarDigital Library
19. Ogniewicz, R., and Ilg, M. 1992. Voronoi skeletons: Theory and applications. In Proceedings on Computer Vision and Pattern Recognition, 63–69.Google Scholar
20. Palágyi, K., and Kuba, A. 1999. A parallel 3D 12-subiteration thinning algorithm. Graph. Models Image Process. 61, 4, 199–221. Google ScholarDigital Library
21. Pascucci, V., Scorzelli, G., Bremer, P.-T., and Mascarenhas, A. 2007. Robust on-line computation of Reeb graphs: simplicity and speed. ACM Trans. Graph. 26, 3, Article 58. Google ScholarDigital Library
22. Sharf, A., Lewiner, T., Shamir, A., and Kobbelt, L. 2007. On-the-fly curve-skeleton computation for 3D shapes. Computer Graphics Forum 26, 3, 323–328.Google ScholarCross Ref
23. Shi, X., Zhou, K., Tong, Y., Desbrun, M., Bao, H., and Guo, B. 2007. Mesh puppetry: cascading optimization of mesh deformation with inverse kinematics. ACM Trans. Graph. 26, 3, Article 81. Google ScholarDigital Library
24. Sorkine, O., and Cohen-Or, D. 2004. Least-squares meshes. In Proceedings of Shape Modeling International, 191–199. Google ScholarDigital Library
25. Wade, L. 2000. Automated generation of control skeletons for use in animation. PhD thesis. Adviser-Richard E. Parent. Google ScholarDigital Library
26. Wang, Y.-S., and Lee, T.-Y. 2008. Curve skeleton extraction using iterative least squares optimization. IEEE Transactions on Visualization and Computer Graphics. Google ScholarDigital Library
27. Wang, R. Y., Pulli, K., and Popović, J. 2007. Real-time enveloping with rotational regression. ACM Trans. Graph. 26, 3, Article 73. Google ScholarDigital Library
28. Weber, O., Sorkine, O., Lipman, Y., and Gotsman, C. Context-aware skeletal shape deformation. Computer Graphics Forum 26, 3, 265–274.Google Scholar
29. Yoshizawa, S., Belyaev, A., and Seidel, H.-P. 2007. Skeleton-based variational mesh deformations. Computer Graphics Forum 26, 3, 255–264.Google ScholarCross Ref
30. Zhou, Y., and Toga, A. W. 1999. Efficient skeletonization of volumetric objects. IEEE Transactions on Visualization and Computer Graphics 5, 3, 196–209. Google ScholarDigital Library