“Simulating facial surgery using finite element models” by Koch, Gross, Carls, von Büren, Fankhauser, et al. …

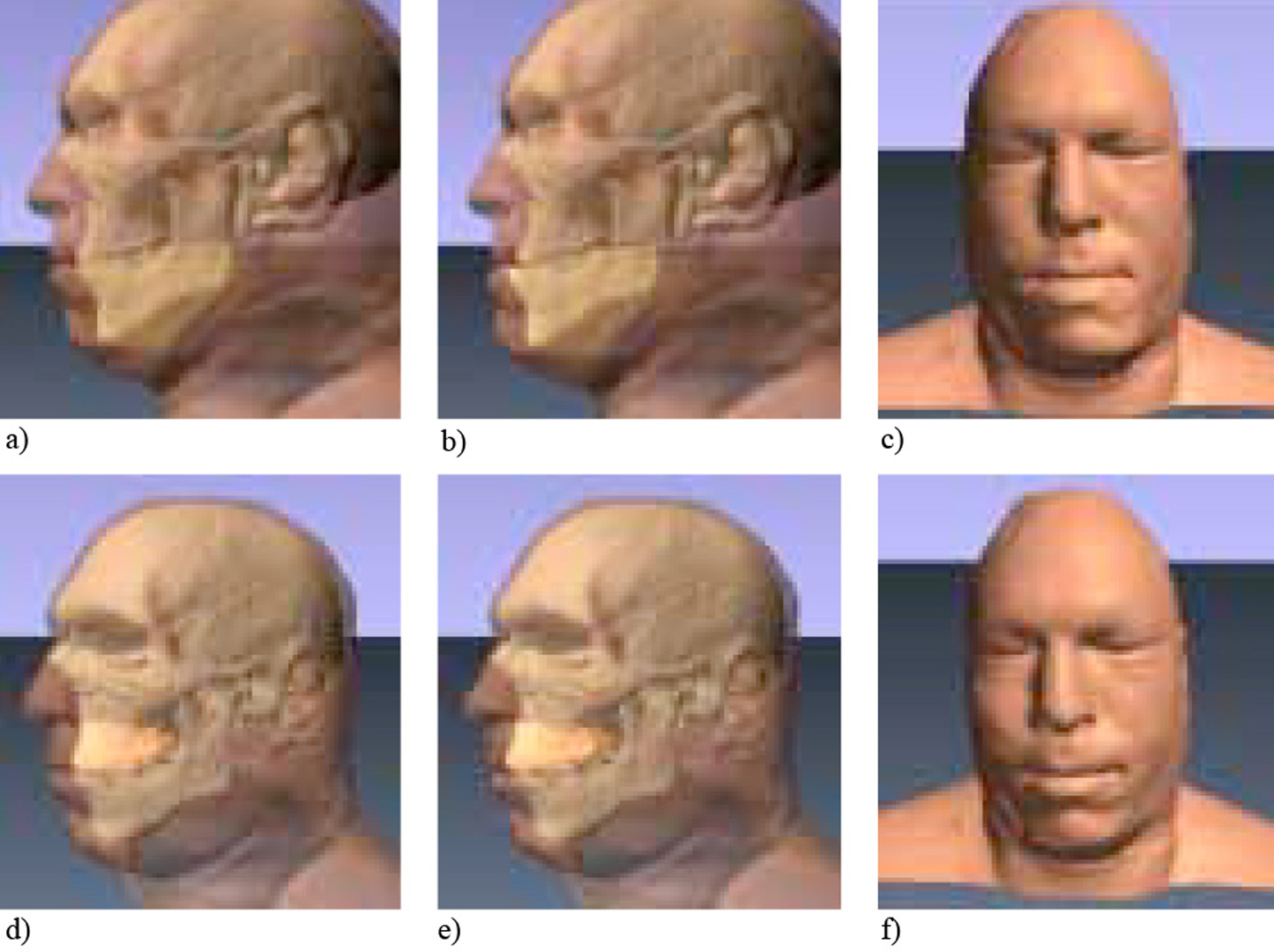
This paper describes a prototype system for surgical planning and prediction of human facial shape after craniofacial and maxillofacial surgery for patients with facial deformities. For this purpose it combines, unifies, and extends various methods from geometric modeling, finite element analysis, and image processing to render highly realistic 3D images of the post surgical situation. The basic concept of the system is to join advanced geometric modeling and animation systems such as Alias with a special purpose finite element model of the human face developed under AVS. In contrast to existing facial models we acquire facial surface and soft tissue data both from photogrammetric and CT scans of the individual. After initial data preprocessing, reconstruction, and registration, a finite element model of the facial surface and soft tissue is provided which is based on triangular finite elements. Stiffness parameters of the soft tissue are computed using segmentations of the underlying CT data. All interactive procedures such as bone and soft tissue repositioning are performed under the guidance of the modeling system which feeds the processed geometry into the FEM solver. The resulting shape is generated from minimizing the global energy of the surface under the presence of external forces. Photorealistic pictures are obtained from rendering the facial surface with the advanced animation system on which this prototype is built. Although we do not claim any of the presented algorithms themselves to be new, the synthesis of several methods offers a new facial model quality. Our concept is a significant extension to existing ones and, due to its versatility, can be employed in different applications such as facial animation, facial reconstruction, or the simulation of aging. We illustrate features of our system with some examples from the Visible Human Data Set.TM

1. CANNY, J. F. A computational approach to edge detection. IEEE Transactions on Pattern Analysis and Machine Intelligence 8, 6 (1986), pp. 679-697.
2. CELNIKER, G., AND GOSSARD, D. Deformable curve and surface finite elements for free-form shape design. In Compuwr Graphics (SIGGRAPH ’91 Proceedings) (July 1991), ACM SIGGRAPH, T. W. Sederberg, Ed., vol. 25, pp. 257- 266.
3. DREBIN, R. A., CARPENTER, L., AND HANRAHAN, P. Volume rendering. In Computer Graphics (SIGGRAPH ’88 Proceedings) (Aug. 1988), ACM SIGGRAPH, J. Dill, Ed., vol. 22, pp. 65-74.
4. FARKAS, L. G. Anth~vpometry of the Head and Face, second ed. Raven Press, 1994.
5. GROSS, M. U., GATTI, e., AND STAADT, O. Fast multiresolution surface meshing. In Proceedings oflEEE Visualization ’95 (1995), IEEE Computer Society Press, pp. 135-142.
6. GROSS, M. U., AND KOCH, e. Visualization of multidimensional shape and texture features in laser range data using complex-valued Gabor wavelets. IEEE Transactions on Visualization and Computer Graphics 1, 1 (Mar. 1995), pp. 44-59. ISSN 1077-2626.
7. HANRAHAN, P., AND KRUEGER, W. Reflection from layered surfaces due to subsurface scattering. In Computer Graphics (SIGGRAPH ’93 Proceedings) (Aug. 1993), ACM SIC- GRAPH, J. T. Kajiya, Ed., vol. 27, pp. 165-174.
8. HARALICK, R. M., AND SHAPIRO, L. G. Computer and Robot Vision, vol. 1-3. Addison-Wesley, 1992.
9. KUNDERT, K. S., AND SANGIOVANNI-VINCENTELLI, A. A Sparse Linear Equation Solver. Dept. of Electrical Engineering and Computer Sciences, University of California, Berkeley, 1988.
10. LEE, Y., TERZOPOULOS, D., AND WATERS, K. Realistic face modeling for animation. In Computer Graphics (SIC- GRAPH ’95 Proceedings) (Aug. 1995), ACM SIGGRAPH, R. Cook, Ed., vol. 29, pp. 55-62.
11. NATIONAL LIBRARY OF MEDICINE. The Visible Human P~vject. http://www.nlm.nih.gov/extramural_research.dir/visible_human.html, 1995.
12. PARKE, F. I. Parameterized models for facial animation. IEEE Computer Graphics and Applications 2 (Nov. 1982), pp. 61-68.
13. SCHROEDER, W. J., ZARGE, J. A., AND LORENSEN, W. E. Decimation of triangle meshes. In Computer Graphics (SIC- GRAPH ’92 Proceedings) (Aug.1992), ACM SIGGRAPH, E. E. Catmull, Ed., pp. 65-70.
14. VAN GELDER, A., AND WILHELMS, J. Topological considerations in isosurface generation. Tech. Rep. UCSC-CRL-94- 31, Baskin Center for Computer Engineering and Information Sciences, University of California, Santa Cruz, 1994.
15. VANNIER, M. W., PILGRAM, T., BHATIA, G., BRUNSDEN, B., AND COMMEAN, P. Facial surface scanner. IEEE Computer Graphics and Applications 11, 6 (Nov. 1991), pp. 72- 80.
16. WATERS, K. A muscle model for animating three-dimensional facial expression. In Computer Graphics (SIGGRAPH ’87 Proceedings) (July 1987), ACM SIGGRAPH, M. C. Stone, Ed., vol. 21, pp. 17-24.
17. ZIENKIEWICZ, O. C. The Finite Element Method, fourth ed., vol. 1-2. McGraw-Hill, 1994.