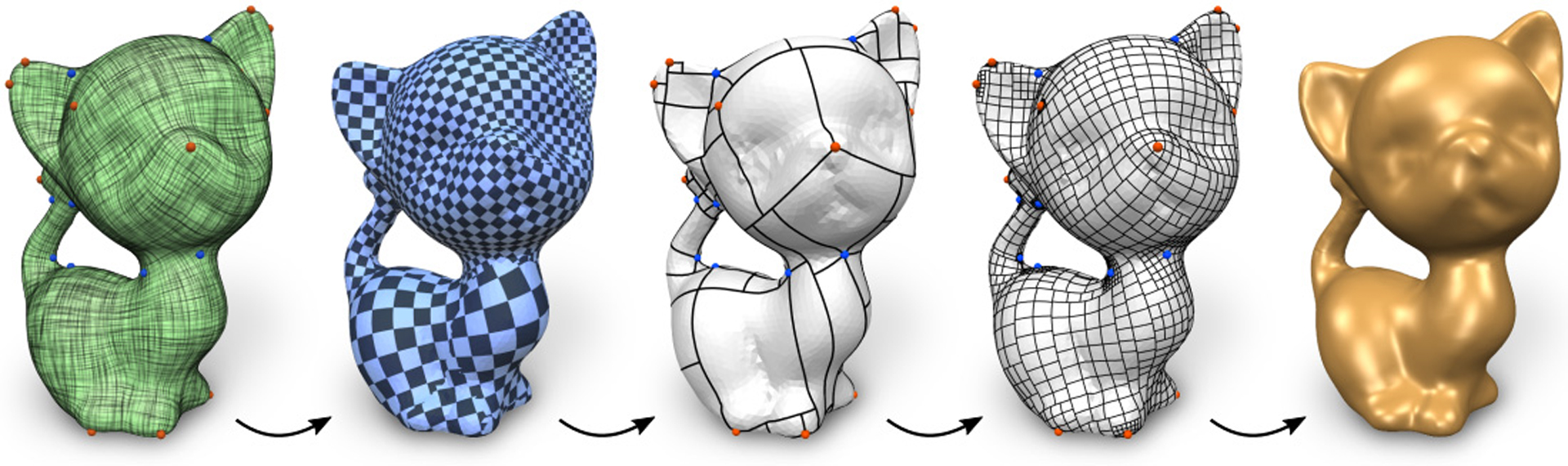
“Similarity maps and field-guided T-splines: a perfect couple” by Campen and Zorin
Conference:
Type(s):
Title:
- Similarity maps and field-guided T-splines: a perfect couple
Session/Category Title: Global Parameterization
Presenter(s)/Author(s):
Moderator(s):
Abstract:
A variety of techniques were proposed to model smooth surfaces based on tensor product splines (e.g. subdivision surfaces, free-form splines, T-splines). Conversion of an input surface into such a representation is commonly achieved by constructing a global seamless parametrization, possibly aligned to a guiding cross-field (e.g. of principal curvature directions), and using this parametrization as domain to construct the spline-based surface.One major fundamental difficulty in designing robust algorithms for this task is the fact that for common types, e.g. subdivision surfaces (requiring a conforming domain mesh) or T-spline surfaces (requiring a globally consistent knot interval assignment) reliably obtaining a suitable parametrization that has the same topological structure as the guiding field poses a major challenge. Even worse, not all fields do admit suitable parametrizations, and no concise conditions are known as to which fields do.We present a class of surface constructions (T-splines with halfedge knots) and a class of parametrizations (seamless similarity maps) that are, in a sense, a perfect match for the task: for any given guiding field structure, a compatible parametrization of this kind exists and a smooth piecewise rational surface with exactly the same structure as the input field can be constructed from it. As a byproduct, this enables full control over extraordinary points. The construction is backward compatible with classical NURBS. We present efficient algorithms for building discrete conformal similarity maps and associated T-meshes and T-spline surfaces.
References:
1. Ralph Abraham, Jerrold E Marsden, and Tudor Ratiu. 1988. Manifolds, Tensor Analysis, and Applications. Springer, New York, NY, USA.Google Scholar
2. Noam Aigerman and Yaron Lipman. 2015. Orbifold Tutte Embeddings. ACM Trans. Graph. 34, 6 (2015), 190:1–190:12.Google ScholarDigital Library
3. Pierre Alliez, David Cohen-Steiner, Olivier Devillers, Bruno Lévy, and Mathieu Desbrun. 2003. Anisotropic polygonal remeshing. ACM Trans. Graph. 22, 3 (2003). Google ScholarDigital Library
4. Thierry Aubin. 1998. Some Nonlinear Problems in Riemannian Geometry. Springer Berlin Heidelberg. Google ScholarCross Ref
5. Yuri Bazilevs, Victor M Calo, John A Cottrell, John A Evans, TJR Hughes, S Lipton, Michael A Scott, and Thomas W Sederberg. 2010. Isogeometric analysis using T-splines. Computer Methods in Applied Mechanics and Eng. 199, 5 (2010), 229–263. Google ScholarCross Ref
6. Mirela Ben-Chen, Craig Gotsman, and Guy Bunin. 2008. Conformal flattening by curvature prescription and metric scaling. In Comp. Graph. Forum, Vol. 27. 449–458. Google ScholarCross Ref
7. Martin Bertram, Mark A. Duchaineau, Bernd Hamann, and Kenneth I. Joy. 2004. Generalized B-Spline Subdivision-Surface Wavelets for Geometry Compression. IEEE TVCG 10, 3 (2004), 326–338. Google ScholarDigital Library
8. Ioana Boier-Martin, Holly Rushmeier, and Jingyi Jin. 2004. Parameterization of triangle meshes over quadrilateral domains. Symp. on Geometry Processing (2004), 193–203. Google ScholarDigital Library
9. David Bommes, Marcel Campen, Hans-Christian Ebke, Pierre Alliez, and Leif Kobbelt. 2013. Integer-grid maps for reliable quad meshing. ACM Trans. Graph. 32, 4 (2013). Google ScholarDigital Library
10. David Bommes, Henrik Zimmer, and Leif Kobbelt. 2009. Mixed-integer quadrangulation. ACM Trans. Graph. 28, 3 (2009), 77. Google ScholarDigital Library
11. Philip L. Bowers and Monica K. Hurdal. 2003. Planar Conformal Mappings of Piecewise Flat Surfaces. Springer Berlin Heidelberg, 3–34.Google Scholar
12. Guy Bunin. 2008. A continuum theory for unstructured mesh generation in two dimensions. Computer Aided Geometric Design 25, 1 (2008), 14–40. Google ScholarDigital Library
13. Marcel Campen, David Bommes, and Leif Kobbelt. 2015. Quantized global parametrization. ACM Trans. Graph. 34, 6 (2015), 192. Google ScholarDigital Library
14. Marcel Campen and Leif Kobbelt. 2014. Quad Layout Embedding via Aligned Parameterization. Comp. Graph. Forum 33, 8 (2014).Google Scholar
15. Marcel Campen and Denis Zorin. 2017. On Discrete Conformal Seamless Similarity Maps. (2017). arXiv:1705.02422Google Scholar
16. Nathan A. Carr, Jared Hoberock, Keenan Crane, and John C. Hart. 2006. Rectangular multi-chart geometry images. In Proc. SGP ’06. 181–190.Google Scholar
17. Thomas J. Cashman. 2012. Beyond Catmull-Clark? A Survey of Advances in Subdivision Surface Methods. Comp. Graph. Forum 31, 1 (2012), 42–61.Google ScholarDigital Library
18. Edward Chien, Zohar Levi, and Ofir Weber. 2016. Bounded Distortion Parametrization in the Space of Metrics. ACM Trans. Graph. 35, 6 (2016), 215:1–215:16.Google ScholarDigital Library
19. Bennett Chow and Feng Luo. 2003. Combinatorial Ricci Flows on Surfaces. J. Differential Geom. 63, 1 (2003), 97–129. Google ScholarCross Ref
20. Keenan Crane, Mathieu Desbrun, and Peter Schröder. 2010. Trivial Connections on Discrete Surfaces. Comp. Graph. Forum 29, 5 (2010), 1525–1533.Google ScholarCross Ref
21. Jiansong Deng, Falai Chen, Xin Li, Changqi Hu, Weihua Tong, Zhouwang Yang, and Yuyu Feng. 2008. Polynomial Splines over Hierarchical T-meshes. Graph. Models 70, 4 (2008), 76–86. Google ScholarDigital Library
22. Mathieu Desbrun, Eva Kanso, and Yiying Tong. 2008. Discrete Differential Forms for Computational Modeling. Birkhäuser Basel, 287–324.Google Scholar
23. Hans-Christian Ebke, Patrick Schmidt, Marcel Campen, and Leif Kobbelt. 2016. Interactively Controlled Quad Remeshing of High Resolution 3D Models. ACM Trans. Graph. 35, 6 (2016), 218:1–218:13.Google ScholarDigital Library
24. Matthias Eck and Hugues Hoppe. 1996. Automatic Reconstruction of B-spline Surfaces of Arbitrary Topological Type. In Proc. (SIGGRAPH ’96). 325–334.Google ScholarDigital Library
25. David Eppstein, Michael T. Goodrich, Ethan Kim, and Rasmus Tamstorf. 2008. Motorcycle Graphs: Canonical Quad Mesh Partitioning. Comp. Graph. Forum 27, 5 (2008), 1477–1486.Google ScholarCross Ref
26. Gerald Farin. 2002. Curves and Surfaces for CAGD: A Practical Guide (5th ed.). Morgan Kaufmann Publishers Inc., San Francisco, CA, USA.Google Scholar
27. Matthew Fisher, Boris Springborn, Peter Schröder, and Alexander I Bobenko. 2007. An algorithm for the construction of intrinsic Delaunay triangulations with applications to digital geometry processing. Computing 81, 2–3 (2007), 199–213.Google ScholarDigital Library
28. Gunther Greiner. 1994. Variational Design and Fairing of Spline Surfaces. Comp. Graph. Forum 13, 3 (1994).Google Scholar
29. Xianfeng Gu, Ying He, Miao Jin, Feng Luo, Hong Qin, and Shing-Tung Yau. 2008. Manifold splines with a single extraordinary point. Computer-Aided Design 40, 6 (2008), 676–690. Google ScholarDigital Library
30. Xianfeng Gu, Feng Luo, Jian Sun, and Tianqi Wu. 2013. A discrete uniformization theorem for polyhedral surfaces. arXiv:1309.4175 (2013).Google Scholar
31. Xianfeng Gu and Shing-Tung Yau. 2003. Global conformal surface parameterization. In Proc. Symposium on Geometry Processing 2003. 127–137.Google Scholar
32. Ying He, Kexiang Wang, Hongyu Wang, Xianfeng Gu, and Hong Qin. 2006. Manifold T-Spline. In Proc. Geometric Modeling and Processing. 409–422.Google Scholar
33. Miao Jin, Junho Kim, and Xianfeng David Gu. 2007. Discrete Surface Ricci Flow: Theory and Applications. 209–232.Google Scholar
34. Ernest Jucovic and Marián Trenkler. 1973. A theorem on the structure of cell-decompositions of orientable 2-manifolds. Mathematika 20, 01 (1973), 63–82. Google ScholarCross Ref
35. Felix Kälberer, Matthias Nieser, and Konrad Polthier. 2007. QuadCover: Surface Parameterization using Branched Coverings. Comp. Graph. Forum 26, 3 (2007), 375–384.Google ScholarCross Ref
36. Kestutis Karciauskas, Daniele Panozzo, and Jörg Peters. 2016. Spline surfaces with T-junctions. (2016). arXiv:1610.05351.Google Scholar
37. Liliya Kharevych, Boris Springborn, and Peter Schröder. 2006. Discrete Conformal Mappings via Circle Patterns. ACM Trans. Graph. 25, 2 (2006), 412–438. Google ScholarDigital Library
38. Andrei Khodakovsky, Peter Schröder, and Wim Sweldens. 2000. Progressive Geometry Compression. In Proc. SIGGRAPH ’00. 271–278. Google ScholarDigital Library
39. Denis Kovacs, Justin Bisceglio, and Denis Zorin. 2015. Dyadic T-mesh Subdivision. ACM Trans. Graph. 34, 4 (2015), 143:1–143:12.Google ScholarDigital Library
40. Wan-Chiu Li, Nicolas Ray, and Bruno Lévy. 2006. Automatic and interactive mesh to T-spline conversion. In Proc. SGP ’06. 191–200.Google ScholarDigital Library
41. Xin Li, Jiansong Deng, and Falai Chen. 2010. Polynomial splines over general T-meshes. The Visual Computer 26, 4 (2010), 277–286. Google ScholarDigital Library
42. Xin Li, G. Thomas Finnigan, and Thomas W. Sederberg. 2016. G1 Non-uniform Catmull-Clark Surfaces. ACM Trans. Graph. 35, 4 (2016), 135:1–135:8.Google ScholarDigital Library
43. Xin Li, Jianmin Zheng, Thomas W. Sederberg, Thomas J. R. Hughes, and Michael A. Scott. 2012. On linear independence of T-spline blending functions. Computer Aided Geometric Design 29, 1 (2012), 63–76. Google ScholarDigital Library
44. Yaron Lipman. 2012. Bounded distortion mapping spaces for triangular meshes. ACM Trans. Graph. 31, 4 (2012), 108. Google ScholarDigital Library
45. Michael Lounsbery, Tony D. DeRose, and Joe Warren. 1997. Multiresolution Analysis for Surfaces of Arbitrary Topological Type. ACM Trans. Graph. 16, 1 (1997), 34–73. Google ScholarDigital Library
46. Feng Luo. 2004. Combinatorial Yamabe flow on surfaces. Communications in Contemporary Mathematics 6, 05 (2004), 765–780. Google ScholarCross Ref
47. Kerstin Müller, Lars Reusche, and Dieter Fellner. 2006. Extended Subdivision Surfaces: Building a Bridge Between NURBS and Catmull-Clark Surfaces. ACM Trans. Graph. 25, 2 (2006), 268–292. Google ScholarDigital Library
48. Ashish Myles, Nico Pietroni, Denis Kovacs, and Denis Zorin. 2010. Feature-aligned T-meshes. ACM Trans. Graph. 29, 4 (2010), 117:1–117:11.Google ScholarDigital Library
49. Ashish Myles, Nico Pietroni, and Denis Zorin. 2014. Robust Field-aligned Global Parametrization. ACM Trans. Graph. 33, 4 (2014). Google ScholarDigital Library
50. Ashish Myles and Denis Zorin. 2012. Global parametrization by incremental flattening. ACM Trans. Graph. 31, 4 (2012), 109. Google ScholarDigital Library
51. Ashish Myles and Denis Zorin. 2013. Controlled-distortion constrained global parametrization. ACM Trans. Graph. 32, 4 (2013), 105. Google ScholarDigital Library
52. Daniele Panozzo, Enrico Puppo, Marco Tarini, Nico Pietroni, and Paolo Cignoni. 2011. Automatic Construction of Quad-Based Subdivision Surfaces Using Fitmaps. IEEE Transactions on Visualization and Computer Graphics 17, 10 (2011), 1510–1520. Google ScholarDigital Library
53. Jörg Peters. 1992. Joining smooth patches around a vertex to form a Ck surface. Computer Aided Geometric Design 9, 5 (1992), 387 — 411. Google ScholarDigital Library
54. M. M. Postnikov. 2001. Geometry VI: Riemannian Geometry. Springer Berlin Heidelberg.Google ScholarCross Ref
55. Nicolas Ray, Wan Chiu Li, Bruno Lévy, Alla Sheffer, and Pierre Alliez. 2006. Periodic Global Parameterization. ACM Trans. Graph. 25, 4 (2006), 1460–1485. Google ScholarDigital Library
56. Nicolas Ray, Vincent Nivoliers, Sylvain Lefebvre, and Bruno Lévy. 2010. Invisible Seams. In Proc. Eurographics Symposium on Rendering. Google ScholarDigital Library
57. Nicolas Ray and Dmitry Sokolov. 2014. Robust Polylines Tracing for N-Symmetry Direction Field on Triangulated Surfaces. ACM Trans. Graph. 33, 3 (2014). Google ScholarDigital Library
58. Nicolas Ray, Bruno Vallet, Wan Chiu Li, and Bruno Lévy. 2008. N-Symmetry direction field design. ACM Trans. Graph. 27 (2008), 2. Google ScholarDigital Library
59. Richard Schoen and Shing-Tung Yau. 1994. Lectures on Differential Geometry. International Press.Google Scholar
60. Thomas W. Sederberg, David L. Cardon, G. Thomas Finnigan, Nicholas S. North, Jianmin Zheng, and Tom Lyche. 2004. T-spline Simplification and Local Refinement. ACM Trans. Graph. 23, 3 (2004), 276–283. Google ScholarDigital Library
61. Thomas W Sederberg, G. Thomas Finnigan, Xin Li, Hongwei Lin, and Heather Ipson. 2008. Watertight trimmed NURBS. ACM Trans. Graph. 27, 3 (2008).Google ScholarDigital Library
62. Thomas W. Sederberg, Jianmin Zheng, Almaz Bakenov, and Ahmad Nasri. 2003. T-splines and T-NURCCs. ACM Trans. Graph. 22, 3 (2003), 477–484. Google ScholarDigital Library
63. Boris Springborn, Peter Schröder, and Ulrich Pinkall. 2008. Conformal equivalence of triangle meshes. ACM Trans. Graph. 27, 3 (2008). Google ScholarDigital Library
64. Jos Stam. 1998. Exact Evaluation of Catmull-Clark Subdivision Surfaces at Arbitrary Parameter Values. In Proc (SIGGRAPH ’98). 395–404. Google ScholarDigital Library
65. Yiying Tong, Pierre Alliez, Daniel Cohen-Steiner, and Mathieu Desbrun. 2006. Designing quadrangulations with discrete harmonic forms. Symposium on Geometry Processing (2006), 201–210.Google ScholarDigital Library
66. Marc Troyanov. 1991. Prescribing curvature on compact surfaces with conical singularities. Trans. Amer. Math. Soc. 324 (1991), 793–821. Google ScholarCross Ref
67. Amir Vaxman, Marcel Campen, Olga Diamanti, Daniele Panozzo, David Bommes, Klaus Hildebrandt, and Mirela Ben-Chen. 2016. Directional Field Synthesis, Design, and Processing. Comp. Graph. Forum 35, 2 (2016).Google Scholar
68. Wenyan Wang, Yongjie Zhang, Guoliang Xu, and Thomas J.R. Hughes. 2012. Converting an unstructured quadrilateral/hexahedral mesh to a rational T-spline. Computational Mechanics 50, 1 (2012), 65–84. Google ScholarDigital Library
69. Denis Zorin, Peter Schröder, and Wim Sweldens. 1997. Interactive Multiresolution Mesh Editing. In Proc. SIGGRAPH ’97. 259–268. Google ScholarDigital Library