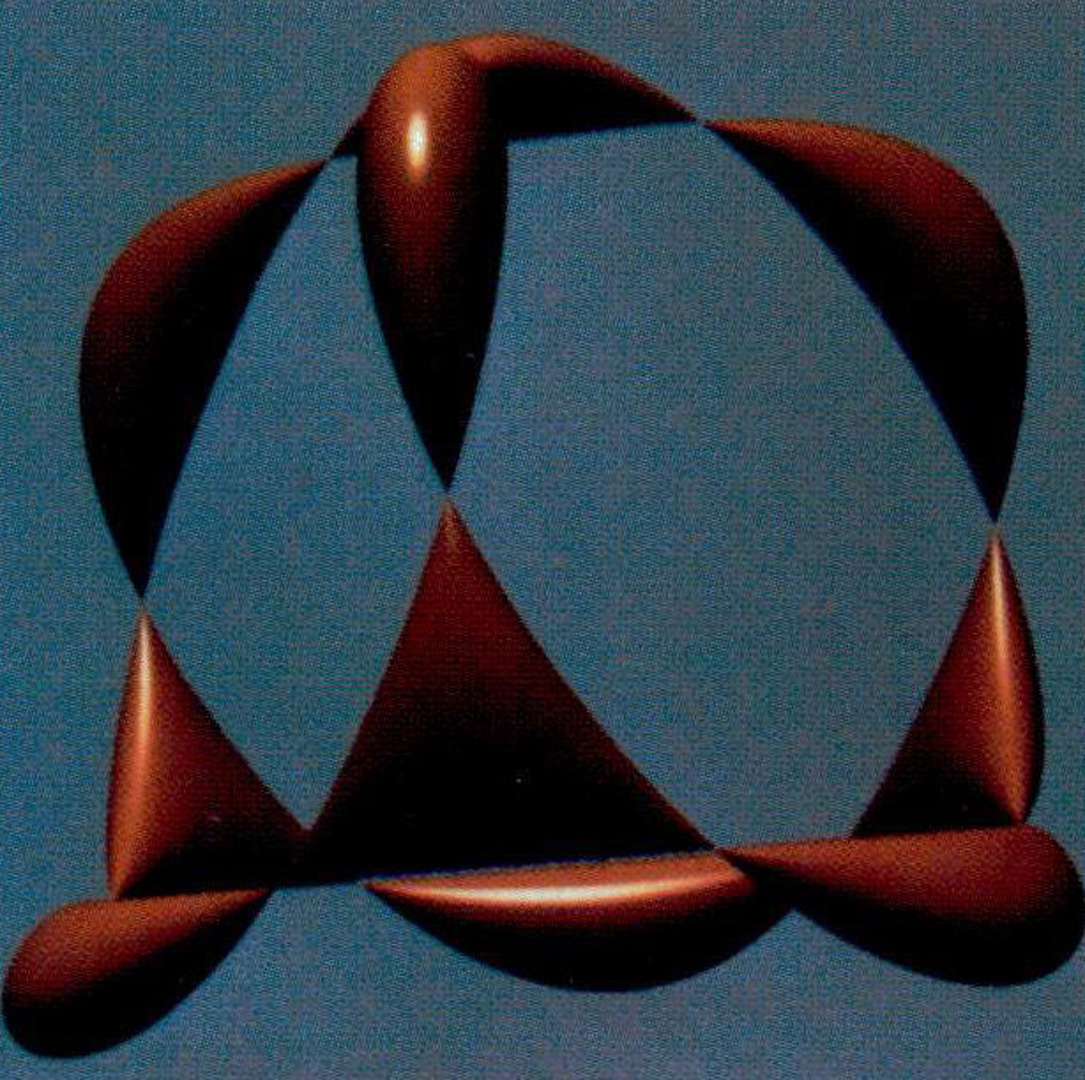“Scan line display of algebraic surfaces” by Sederberg and Zundel

A robust algorithm is presented for scan line display of algebraic surfaces of arbitrary degree and topology. The algorithm correctly displays singularities of any complexity, even those missed by ray tracing or polygonization, and (for surfaces of degree less than eight) offers a significant speed improvement over ray tracing. Antialiasing can generally be accomplished very quickly. In addition to its typical function of shaded raster display, the algorithm is particularly adept at quickly plotting silhouette and intersection curves. A practical use for the algorithm is to display boolean combinations of algebraic half spaces, including blend surfaces.A new polynomial basis is introduced, referred to as the Bernstein pyramid polynomial basis, which enhances numerical stability and which simplifies several computations such as scan planesurface intersection and silhouette detection.

1. Arnon, D.S., Topologically reliable display of algebraic curves, Computer Graphics, 17, 1983, 219-228.
2. Arnon, D.S. and Rauen, J., On the display of cell decompositions of algebraic surfaces, XEROX Technical Report, 1988.
3. Bloomenthal, J., Polygonization of implicit surfaces, Computer Aided Geometric Design, 5, 1988, 341-355.
4. Bradshaw, C.B., Surfaces of functions of three variables, M.S. Thesis, Department of Civil Engineering, Brigham Young University, 1982.
5. Farouki, R.T., The characterization of parametric surface sections, Computer Vision, Graphics and Image Processing, 1986, 33, 209-236.
6. Farouki, R.T. and Rajan, V.T., On the numerical condition of polynomials in Bernstein form, Computer Aided Geometric Design, 4, 1987, 191-216.
7. Farouki, R.T. and Rajan, V.T., Algorithms for polynomials in Bernstein form, Computer Aided Geometric Design, 1988, 5, 1-26.
8. Farin, G., Curves and Surfaces for Computer Aided Geometric Design, Academic Press, 1988.
9. Goldman, R.N., Sederberg, T.W. and Anderson, D.C., Vector elimination: A technique for the implicitization, inversion, and intersection of planar parametric rational polynomial curves, Computer Aided Geometric Design, 1, 1984, 327-356.
10. Hall, M. and Warren, J., Adaptive tessellation of implicitly defined surfaces, Rice COMP TR88-84, 1988, Rice University.
11. Hanrahan, P., Ray tracing algebraic surfaces, Computer Graphics, 17, 3, 1983, 83-90.
12. Hoffmann, C.M. and Hopcroft, I.E., Automatic surface generation in computer aided design, The Visual Con~outer, 1, 1985, 95-100.
13. Lane, J.M. and Riesenfeld, R.F., Bounds on a polynomial, B/T, 21, 1, 1981, 112-117.
14. Mahl, R., Visible surface algorithms for quadric patches, IEEE Transactions on Computers, C.21, 1, 1972, 1-4.
15. Middleditch, A.E. and Sears, K., Blend surfaces for set theoretic volume modeling systems, Computer Graphics, 19, 1985, 161-170.
16. Owen, J.C. and Rockwood, A.P., Intersection of general implicit surfaces. In Geometric Modeling: Algorithms and New Trends, G. Farin, editor, SIAM, Philadelphia, 1987, 335-346.
17. Patrikalakis, N.M. and Kriezis, G.A., Piecewise continuous algebraic surfaces in terms of B-splines, MITSG 88-5, Massachusetts Institute of Technology, August 1988.
18. Petersen, C.S., Adaptive contouring of three-dimensional surfaces, Computer Aided Geometric Design, 1, 1984, 61-74.
19. Rockwood, A.P. and Owen, J.C., Blending surfaces in solid modeling. In Geometrk: Modeling: Algorithms and New Trends, G. Farin, editor, SIAM, Philadelphia, 1987, 335-346.
20. Salmon, G. Analytic Geometry of Three Dimensions, Longmarts, Green and Co., 1912.
21. Sederberg, T.W., Piecewise algebraic surface patches, Computer Aided Geometric Design, 2, 1985, 53-59.
22. Sederberg, T.W. and Parry, S.R., Comparison of three curve intersection algorithms, Computer-Aided Design, 18, 1, (1986), 58-63.
23. Sederberg, T.W., An algorithm for algebraic curve intersection, to appear in, Computer-Aided Design.
24. Sederberg, T.W., Spencer, M.R. and de Boor, C., Real root approximation of polynomials in Bernstein form, in preparation.
25. Tindle, G.L., Tetrahedral triangulation, in, R.R. Martin, ed., The Mathematics of Surfaces H, Clarendon Press, Oxford, 1987, 387-394.
26. Warren, J.D., On algebraic surfaces meeting with geometric continuity, Ph.D. Thesis, Cornell University, 1986.
27. Weiss, R.A., BE VISION, A package of IBM 7090 FOR- TRAN programs to draw orthographic views of combinations of plane and quadric surfaces, JACM, 13, 2, 1966, 194-204.
28. Zundel, A.K., Scan line rendering of algebraic surfaces and half spaces, M.S. Thesis, Department of Civil Engineering, Brigham Young University, 1989.