“Robust repair of polygonal models” by Ju

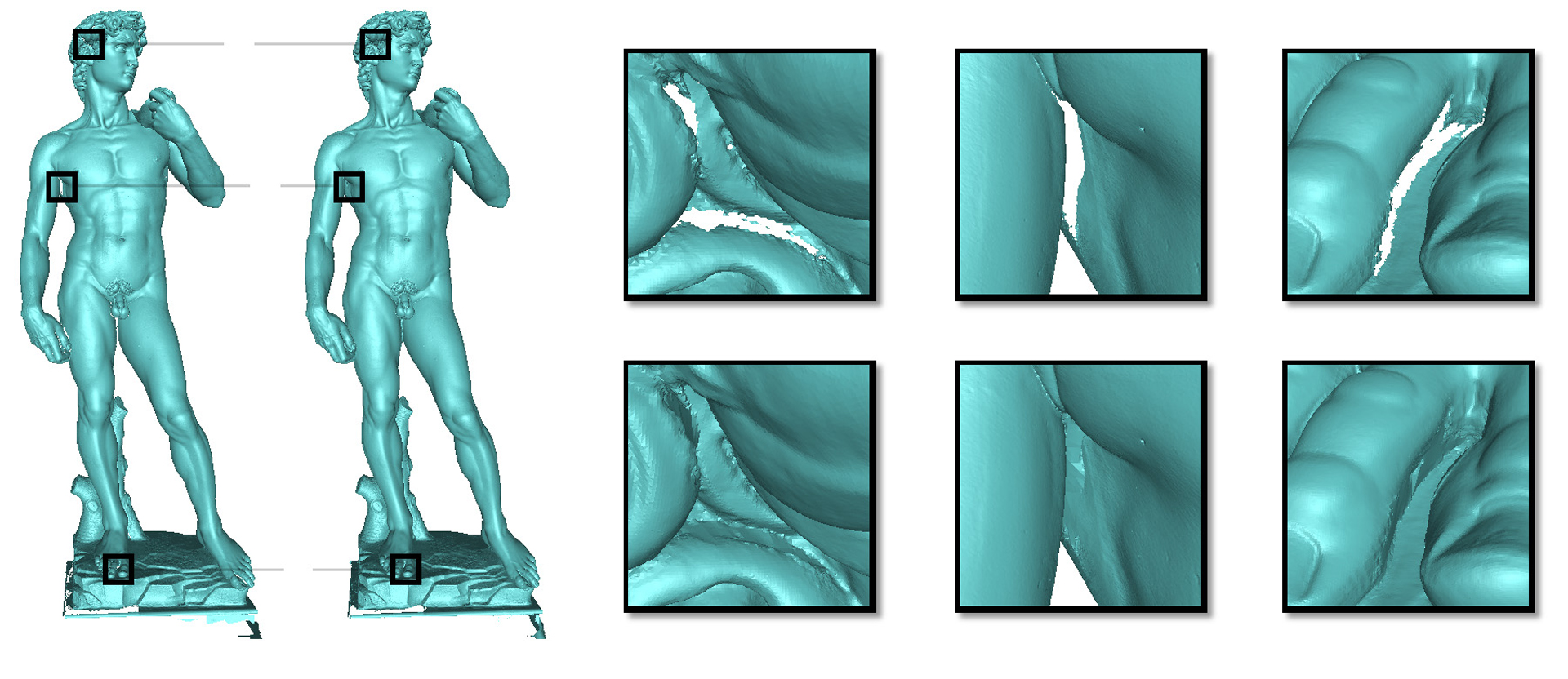
We present a robust method for repairing arbitrary polygon models. The method is guaranteed to produce a closed surface that partitions the space into disjoint internal and external volumes. Given any model represented as a polygon soup, we construct an inside/outside volume using an octree grid, and reconstruct the surface by contouring. Our novel algorithm can efficiently process large models containing millions of polygons and is capable of reproducing sharp features in the original geometry.

1. ANDUJAR, C., BRUNET, P., AND AYALA, D. 2002. Topology-reducing surface simplification using a discrete solid representation. ACM Transaction on Graphics 21, 2, 88–105. Google ScholarDigital Library
2. ANDUJAR, C. 1998. Space efficient connectivity test of n-dimensional images. Computer & Graphics 22, 4, 557–558.Google ScholarCross Ref
3. BAREQUET, G., AND KUMAR, S. 1997. Repairing CAD models. In IEEE Visualization ’97, R. Yagel and H. Hagen, Eds., 363–370. Google ScholarDigital Library
4. BOLLOBAS, B. 1979. Graph Theory: An Introductory Course. New York: Springer-Verlag.Google ScholarCross Ref
5. BORODIN, P., NOVOTNI, M., AND KLEIN, R. 2002. Progressive gap closing for mesh repairing. In Advances in Modelling, Animation and Rendering, J. Vince and R. Earnshaw, Eds. Springer Verlag, July, 201–213.Google Scholar
6. BRUNET, P., AND NAVAZO, I. 1990. Solid representation and operation using extended octrees. ACM Transactions on Graphics 9, 2, 170–197. Google ScholarDigital Library
7. COHEN, J., VARSHNEY, A., MANOCHA, D., TURK, G., WEBER, H., AGARWAL, P., BROOKS, F., AND WRIGHT, W. 1996. Simplification envelopes. In Proceedings of ACM SIGGRAPH 1996, ACM Press / ACM SIGGRAPH, New York, E. Fiume, Ed., Computer Graphics Proceedings, Annual Conference Series, ACM, 119–128. Google ScholarDigital Library
8. CURLESS, B., AND LEVOY, M. 1996. A volumetric method for building complex models from range images. In Proceedings of ACM SIGGRAPH 1996, ACM Press / ACM SIGGRAPH, New York, E. Fiume, Ed., Computer Graphics Proceedings, Annual Conference Series, ACM, vol. 30, 303–312. Google ScholarDigital Library
9. DACHILLE, F., AND KAUFMAN, A. 2000. Incremental triangle voxelization. In Graphics Interface, 205–212.Google Scholar
10. DAVIS, J., MARSCHNER, S. R., GARR, M., AND LEVOY, M. 2002. Filling holes in complex surfaces using volumetric diffusion. In First ‘International Symposium on 3D Data Processing, Visualization, and Transmission.Google Scholar
11. DOUGLAS, J. 1931. Solution of the problem of plateau. Transactions of the American Mathematical Society 33, 263–321.Google ScholarCross Ref
12. FOLEY, J. D., VAN DAM, A., FEINER, S. K., AND HUGHES, J. F. 1990. Computer Graphics (2nd Edition). Addison-Wesley Publication Company. Google ScholarDigital Library
13. FRISKEN, S. F., PERRY, R. N., ROCKWOOD, A. P., AND JONES, T. R. 2000. Adaptively sampled distance fields: A general representation of shape for computer graphics. In SProceedings of ACM SIGGRAPH 2000, ACM Press / ACM SIGGRAPH, New York. E. Fiume, Ed., Computer Graphics Proceedings, Annual Conference Series, ACM, K. Akeley, Ed., 249–254. Google ScholarDigital Library
14. GARLAND, M., AND HECKBERT, P. S. 1997. Surface simplification using quadric error metrics. In Proceedings of ACM SIGGRAPH 1997, ACM Press / ACM SIGGRAPH, New York. E. Fiume, Ed., Computer Graphics Proceedings, Annual Conference Series, ACM, 209–216. Google ScholarDigital Library
15. GOTTSCHALK, S. 1996. Separating axis theorem. Technical Report TR96-024, Dept. of Computer Science, UNC Chapel Hill.Google Scholar
16. GUEZIEC, A., TAUBIN, G., LAZARUS, F., AND HORN, W. 1998. Converting sets of polygons to manifold surfaces by cutting and stitching. In Proceedings of the conference on Visualization ’98, IEEE Computer Society Press, 383–390. Google ScholarDigital Library
17. HOPPE, H., DEROSE, T., DUCHAMP, T., MCDONALD, J., AND STUETZLE, W. 1992. Surface reconstruction from unorganized points. In Computer Graphics (Proceedings of ACM SIGGRAPH 92), ACM, 71–78. Google ScholarDigital Library
18. HUANG, J., YAGEL, R., FILIPPOV, V., AND KURZION, Y. 1998. An accurate method for voxelizing polygon meshes. In IEEE Symposium on Volume Visualization, 119–126. Google ScholarDigital Library
19. JU, T., LOSASSO, F., SCHAEFER, S., AND WARREN, J. 2002. Dual contouring of hermite data. ACM Transactions on Graphics 21, 3, 339–346. Google ScholarDigital Library
20. KOBBELT, L. P., BOTSCH, M., SCHWANECKE, U., AND SEIDEL, H.-P. 2001. Feature sensitive surface extraction from volume data. In Proceedings of ACM SIGGRAPH 2001, ACM Press / ACM SIGGRAPH, New York, E. Fiume, Ed., Computer Graphics Proceedings, Annual Conference Series, ACM, 57–66. Google ScholarDigital Library
21. LIEPA, P. 2003. Filling holes in meshes. In Proceedings of the Eurographics/ACM SIGGRAPH symposium on Geometry processing, Eurographics Association, 200–205. Google ScholarDigital Library
22. LORENSEN, W., AND CLINE, H. 1987. Marching cubes: A high resolution 3D surface construction algorithm. In Computer Graphics (Proceedings of ACM SIGGRAPH 87), ACM Press, vol. 21, 163–169. Google ScholarDigital Library
23. MURALI, T. M., AND FUNKHOUSER, T. A. 1997. Consistent solid and boundary representations from arbitrary polygonal data. In Proceedings of the 1997 symposium on Interactive 3D graphics, ACM Press, 155–ff. Google ScholarDigital Library
24. NOORUDDIN, F. S., AND TURK, G. 2003. Simplification and repair of polygonal models using volumetric techniques. IEEE Transactions on Visualization and Computer Graphics 9, 2, 191–205. Google ScholarDigital Library
25. OHTAKE, Y., BELYAEV, A., ALEXA, M., TURK, G., AND SEIDEL, H.-P. 2003. Multi-level partition of unity implicits. ACM Transactions on Graphics 22, 3, 463–470. Google ScholarDigital Library
26. OOMES, S., SNOEREN, P., AND DIJKSTRA, T. 1997. 3D shape representation: Transforming polygons into voxels. In ScaleSpace97. Google ScholarDigital Library
27. SCHROEDER, W. J., ZARGE, J. A., AND LORENSEN, W. E. 1992. Decimation of triangle meshes. In Computer Graphics (Proceedings of ACM SIGGRAPH 92), ACM Press, 65–70. Google ScholarDigital Library
28. TURK, G., AND LEVOY, M. 1994. Zippered polygon meshes from range images. In Proceedings of ACM SIGGRAPH 1994, ACM Press / ACM SIGGRAPH, New York. E. Fiume, Ed., Computer Graphics Proceedings, Annual Conference Series, ACM, 311–318. Google ScholarDigital Library
29. VARADHAN, G., KRISHNAN, S., KIM, Y. J., AND MANOCHA, D. 2003. Feature-sensitive subdivision and isosurface reconstruction. In 14th IEEE Visualization Conference, 99–106. Google ScholarDigital Library
30. WOOD, Z., HOPPE, H., DESBRUN, M., AND SCHRODER, P. 2002. Isosurface topology simplification. Technical Report MSR-TR-2002-28, Microsoft Research (January).Google Scholar