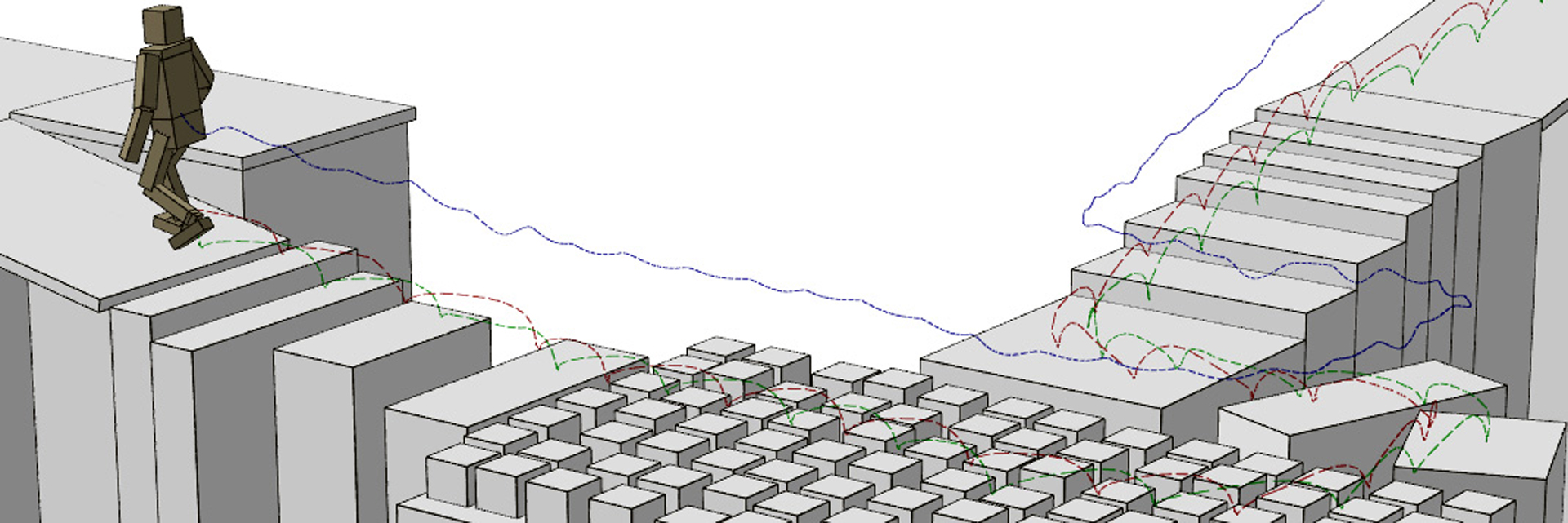
“Robust physics-based locomotion using low-dimensional planning” by Mordatch, De Lasa and Hertzmann

This paper presents a physics-based locomotion controller based on online planning. At each time-step, a planner optimizes locomotion over multiple phases of gait. Stance dynamics are modeled using a simplified Spring-Load Inverted (SLIP) model, while flight dynamics are modeled using projectile motion equations. Full-body control at each instant is optimized to match the instantaneous plan values, while also maintaining balance. Different types of gaits, including walking, running, and jumping, emerge automatically, as do transitions between different gaits. The controllers can traverse challenging terrain and withstand large external disturbances, while following high-level user commands at interactive rates.

1. Abe, Y., da Silva, M., and Popović, J. 2007. Multiobjective Control with Frictional Contacts. In Proc. SCA, 249–258. Google ScholarDigital Library
2. Adamczyk, P. G., Collins, S. H., and Kuo, A. D. 2006. The advantages of a rolling foot in human walking. J. Exp. Biology 209, 3953–3963.Google ScholarCross Ref
3. Alexander, R. M. 1980. Optimum walking techniques for quadrupeds and bipeds. J. Zoology 192, 97–117.Google ScholarCross Ref
4. Chestnutt, J. 2007. Navigation Planning for Legged Robots. PhD thesis, Carnegie Mellon University.Google Scholar
5. Collins, S., Ruina, A., Tedrake, R., and Wisse, M. 2005. Efficient Bipedal Robots Based on Passive Dynamic Walkers. Science 307, 1082–1085.Google ScholarCross Ref
6. Coros, S., Beaudoin, P., and van de Panne, M. 2009. Robust Task-based Control Policies for Physics-based Characters. ACM Trans. Graphics 28, 5, 170. Google ScholarDigital Library
7. da Silva, M., Abe, Y., and Popović, J. 2008. Interactive Simulation of Stylized Human Locomotion. ACM Trans. Graphics 27, 3, 82. Google ScholarDigital Library
8. da Silva, M., Yeuhi, A., and Popović, J. 2008. Simulation of Human Motion Data using Short-Horizon Model-Predictive Control. Proc. Eurographics 27, 2.Google ScholarCross Ref
9. de Lasa, M., Mordatch, I., and Hertzmann, A. 2010. Feature-Based Locomotion Controllers. ACM Trans. Graphics 29, 3. Google ScholarDigital Library
10. Faloutsos, P., van de Panne, M., and Terzopoulos, D. 2001. Composable controllers for physics-based character animation. In Proc. SIGGRAPH, 251–260. Google ScholarDigital Library
11. Full, R. J., and Koditschek, D. E. 1999. Templates and anchors: Neuromechanical hypotheses of legged locomotion on land. J. Exp. Biology 202, 3325–3332.Google Scholar
12. Hansen, N. 2006. The CMA Evolution Strategy: A Comparing Review. In Towards a New Evolutionary Computation: Advances on Estimation of Distribution Algorithms. 75–102.Google Scholar
13. Hodgins, J. K., Wooten, W. L., Brogan, D. C., and O’Brien, J. F. 1995. Animating human athletics. In Proc. SIGGRAPH, 71–78. Google ScholarDigital Library
14. Kajita, S., Matsumoto, O., and Saigo, M. 2001. Real-time 3D walking pattern generation for a biped robot with telescopic legs. In Proc. ICRA, 2299–2306.Google Scholar
15. Kajita, S., Kanehiro, F., Kaneko, K., Fujiwara, K., Harada, K., Yokoi, K., and Hirukawa, H. 2003. Biped Walking Pattern Generation by using Preview Control of Zero-Moment Point. In Proc. ICRA, 1620–1626.Google Scholar
16. Kuffner, J., Nishikawa, K., Kagami, S., Inaba, M., and Inoue, H. 2003. Motion Planning for Humanoid Robots. In Proc. ISRR, 365–374.Google Scholar
17. Laszlo, J., van de Panne, M., and Fiume, E. 1996. Limit cycle control and its application to the animation of balancing and walking. In Proc. SIGGRAPH, 155–162. Google ScholarDigital Library
18. Liu, C. K., Hertzmann, A., and Popović, Z. 2005. Learning Physics-Based Motion Style with Nonlinear Inverse Optimization. ACM Trans. Graphics 24, 3, 1071–1081. Google ScholarDigital Library
19. Macchietto, A., Zordan, V., and Shelton, C. 2009. Momentum Control for Balance. ACM Trans. Graphics 28, 3, 80. Google ScholarDigital Library
20. McGeer, T. 1990. Passive Dynamic Walking. Int. J. Robotics Research 9, 2, 62–82. Google ScholarDigital Library
21. Muico, U., Lee, Y., Popović, J., and Popović, Z. 2009. Contact-aware Nonlinear Control of Dynamic Characters. ACM Trans. Graphics 28, 3, 81. Google ScholarDigital Library
22. Pratt, J., and Tedrake, R. 2005. Velocity-Based Stability Margins for Fast Bipedal Walking. In Fast Motions in Robotics and Biomechanics–Optimization and Feedback Control, vol. 340, 299–324.Google ScholarCross Ref
23. Pratt, J., Carff, J., Drakunov, S., and Goswami, A. 2006. Capture Point: A Step toward Humanoid Push Recovery. In Proc. Humanoid Robots, 200–207.Google Scholar
24. Raibert, M. H., and Hodgins, J. K. 1991. Animation of dynamic legged locomotion. In Proc. SIGGRAPH 1991, 349–358. Google ScholarDigital Library
25. Ramamoorthy, S., and Kuipers, B. 2008. Trajectory Generation for Dynamic Bipedal Walking through Qualitative Model Based Manifold Learning. In Proc. ICRA, 359–366.Google Scholar
26. Rebula, J., Canas, F., Pratt, J., and Goswami, A. 2007. Learning Capture Points for Humanoid Push Recovery. In Proc. Humanoid Robots, 65–72.Google Scholar
27. Schwind, W. J., and Koditschek, D. R. 2000. Approximating the stance map of a 2-DOF monoped runner. J. Nonlinear Science, 533–568.Google Scholar
28. Sok, K. W., Kim, M., and Lee, J. 2007. Simulating Biped Behaviors from Human Motion Data. ACM Trans. Graphics 26, 3, 107. Google ScholarDigital Library
29. Srinivasan, M., and Ruina, A. 2006. Computer optimization of a minimal biped model discovers walking and running. Nature 439, 7072, 72–75.Google Scholar
30. Tsai, Y.-Y., Lin, W.-C., Cheng, K. B., Lee, J., and Lee, T.-Y. 2010. Real-Time Physics-Based 3D Biped Character Animation Using an Inverted Pendulum Model. Trans. Visualization and Computer Graphics 16, 325–337. Google ScholarDigital Library
31. Wampler, K., and Popović, Z. 2009. Optimal Gait and Form for Animal Locomotion. ACM Trans. Graphics 28, 3, 60. Google ScholarDigital Library
32. Witkin, A., and Kass, M. 1988. Spacetime Constraints. In Proc. SIGGRAPH, vol. 22, 159–168. Google ScholarDigital Library
33. Yamane, K., and Hodgins, J. 2009. Simultaneous Tracking and Balancing of Humanoid Robots for Imitating Human Motion Capture Data. Proc. IROS, 2510–2517. Google ScholarDigital Library
34. Yin, K., Loken, K., and van de Panne, M. 2007. SIMBI-CON: Simple Biped Locomotion Control. ACM Trans. Graphics 26, 3, 81. Google ScholarDigital Library