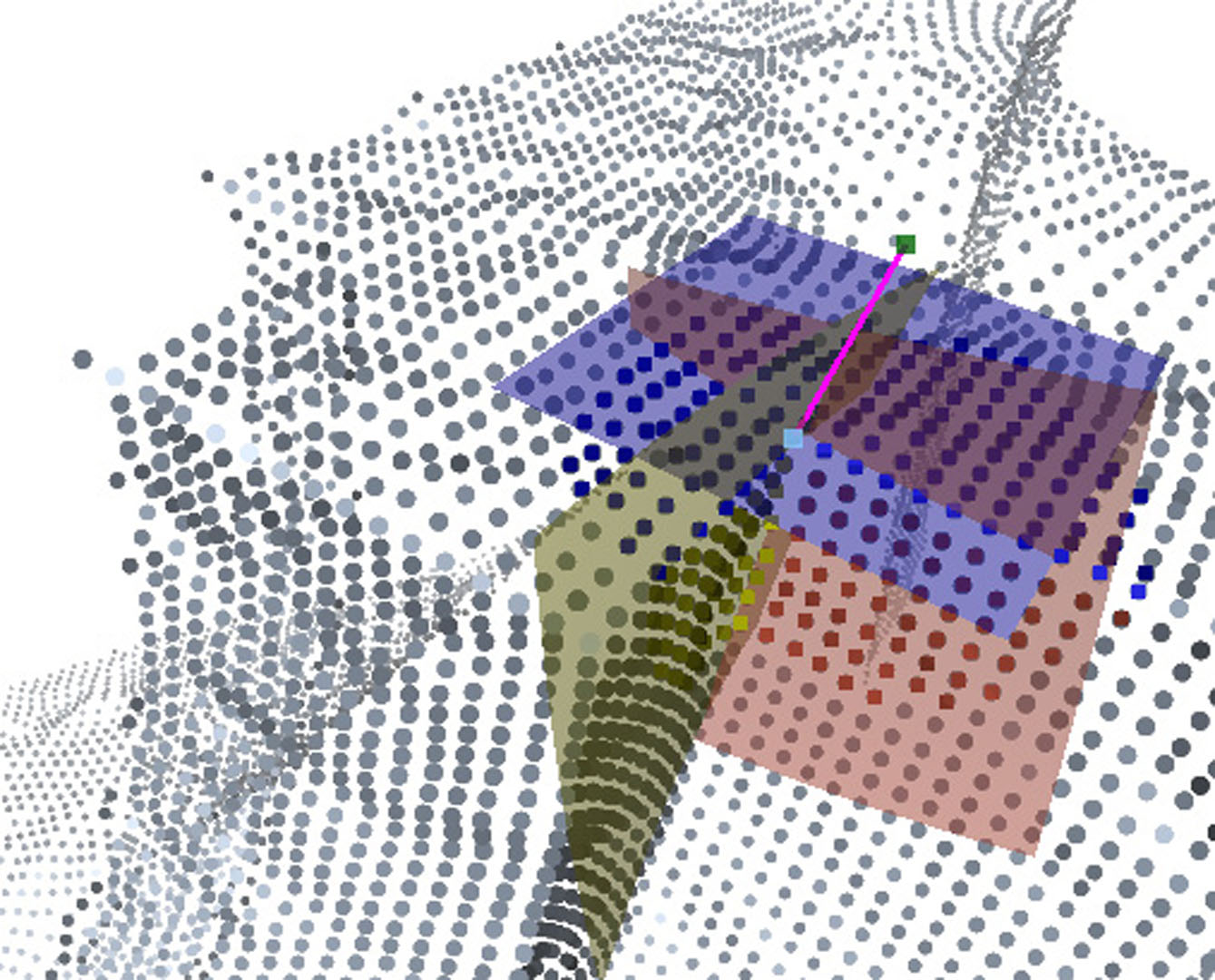
“Robust moving least-squares fitting with sharp features” by Fleishman, Cohen-Or and Silva
Conference:
Type(s):
Title:
- Robust moving least-squares fitting with sharp features
Presenter(s)/Author(s):
Abstract:
We introduce a robust moving least-squares technique for reconstructing a piecewise smooth surface from a potentially noisy point cloud. We use techniques from robust statistics to guide the creation of the neighborhoods used by the moving least squares (MLS) computation. This leads to a conceptually simple approach that provides a unified framework for not only dealing with noise, but also for enabling the modeling of surfaces with sharp features.Our technique is based on a new robust statistics method for outlier detection: the forward-search paradigm. Using this powerful technique, we locally classify regions of a point-set to multiple outlier-free smooth regions. This classification allows us to project points on a locally smooth region rather than a surface that is smooth everywhere, thus defining a piecewise smooth surface and increasing the numerical stability of the projection operator. Furthermore, by treating the points across the discontinuities as outliers, we are able to define sharp features. One of the nice features of our approach is that it automatically disregards outliers during the surface-fitting phase.
References:
1. Alexa, M., Behr, J., Cohen-Or, D., Fleishman, S., Levin, D., and Silva, C. T. 2001. Point set surfaces. In IEEE Visualization 2001, 21–28.]] Google ScholarDigital Library
2. Amenta, N., and Kil, Y. J. 2004. The domain of a point set surface. In Eurographics Symposium on Point-Based Graphics, 139–147.]] Google ScholarDigital Library
3. Amenta, N., and Kil, Y. J. 2004. Defining point-set surfaces. ACM Transactions on Graphics (Proceedings of ACM SIGGRAPH 2004) 23, 3, 264–270.]] Google ScholarDigital Library
4. Amenta, N., Bern, M., and Kamvysselis, M. 1998. A new voronoi-based surface reconstruction algorithm. In ACM SIGGRAPH 1998, 415–422.]] Google ScholarDigital Library
5. Atkinson, A. C., and Riani, M. 2000. Robust Diagnostic Regression Analysis. Springer.]]Google Scholar
6. Bernardini, F., Mittleman, J., Rushmeier, H., Silva, C., and Taubin, G. 1999. The ball-pivoting algorithm for surface reconstruction. IEEE Transactions on Visualization and Computer Graphics 5, 4, 349–359.]] Google ScholarDigital Library
7. Black, M. J., and Sapiro, G. 1999. Edges as outliers: Anisotropic smoothing using local image statistics. In 2nd Conf. on Scale-Space Theories in Computer Vision, 259–270.]] Google ScholarDigital Library
8. Carr, J. C., Beatson, R. K., Cherrie, J. B., Mitchell, T. J., Fright, W. R., Mccallum, B. C., and Evans, T. R. 2001. Reconstruction and representation of 3d objects with radial basis functions. In ACM SIGGRAPH 2001, 67–76.]] Google ScholarDigital Library
9. Clarenz, U., Diewald, U., and Rumpf. M. 2000. Anisotropic geometric diffusion in surface processing. In IEEE Visualization 2000, 397–405.]] Google ScholarDigital Library
10. Curless, B., and Levoy, M. 1996. A volumetric method for building complex models from range images. In ACM SIGGRAPH 1996, 303–312.]] Google ScholarDigital Library
11. Desbrun, M., Meyer, M., Schröder, P., and Barr, A. H. 1999. Implicit fairing of irregular meshes using diffusion and curvature flow. In ACM SIGGRAPH 1999, 317–324.]] Google ScholarDigital Library
12. Dey, T. to appear. Cams/Dimacs Volume On Computer-Aided Design and Manufacturing. American Mathematical Society, ch. Sample Based Geometric Modeling.]]Google Scholar
13. Dinh, H. Q., Turk, G., and Slabaugh, G. 2001. Reconstructing surfaces using anisotropic basis functions. In ICCV 2001, 606–613.]]Google Scholar
14. Fleishman, S., Alexa, M., Cohen-Or, D., and Silva, C. T. 2003. Progressive point set surfaces. ACM Transactions on Graphics 22, 4, 997–1011.]] Google ScholarDigital Library
15. Fleishman, S., Drori, I., and Cohen-Or. D. 2003. Bilateral mesh denoising. ACM Transactions on Graphics (Proceedings of ACM SIGGRAPH 2003) 22, 3, 950–953.]] Google ScholarDigital Library
16. Hadi, A. S. 1992. Identifying multiple outliers in multivariate data. Journal of the Royal Statistical Society: Series B 54, 3, 761–771.]]Google Scholar
17. Hoppe, H., Derose, T., Duchamp, T., Halstead, M., Jin, H., McDonald, J., Schweitzer, J., and Stuetzle, W. 1994. Piecewise smooth surface reconstruction. In ACM SIGGRAPH 1994, 295–302.]] Google ScholarDigital Library
18. Huber, P. J. 1981. Robust Statistics. Wiley, New York (NY).]]Google Scholar
19. Jones, T. R., Durand, F., and Desbrun, M. 2003. Noniterative, feature-preserving mesh smoothing. ACM Transactions on Graphics 22, 3, 943–949.]] Google ScholarDigital Library
20. Ju, T., Losasso, F., Schaefer, S., and Warren, J. 2002. Dual contouring of hermite data. In ACM Transactions on Graphics (Proceedings of ACM SIGGRAPH 2002), 339–346.]] Google ScholarDigital Library
21. Kobbelt, L. P., Botsch, M., Schwanecke, U., and Seidel, H.-P. 2001. Feature sensitive surface extraction from volume data. In ACM SIGGRAPH 2001, 57–66.]] Google ScholarDigital Library
22. Levin, D. 2003. Mesh-independent surface interpolation. In Geometric Modeling for Scientific Visualization. Spinger-Verlag, 37–49.]]Google Scholar
23. Mederos, B., Velho, L., and Figueiredo, L. 2003. Moving least squares multiresolution surface approximation. In XVI Brazilian Symposium on Computer Graphics and Image, 19–26.]]Google Scholar
24. Meer, P., Mintz, D., Kim, D. Y., and Rosenfeld, A. 1991. Robust regression methods for computer vision: A review. International Journal of Computer Vision 6, 1, 59–70.]] Google ScholarDigital Library
25. Miller, J. V., and Stewart, C. V. 1996. Muse: Robust surface fitting using unbiased scale estimates. In CVPR ’96, 300.]] Google ScholarDigital Library
26. Morse, B. S., Yoo, T. S., Rheingans, P., Chen, D. T., and Subramanian, K. R. 2001. Interpolating implicit surfaces from scattered surface data using compactly supported radial basis functions. In Proceedings of the International Conference on Shape Modeling and Applications, 89–98.]] Google ScholarDigital Library
27. Ohtake, Y., Belyaev, A., Alexa, M., Turk, G., and Seidel, H.-P. 2003. Multi-level partition of unity implicits. ACM Transactions on Graphics (Proceedings of ACM SIGGRAPH 2003) 22, 3, 463–470.]] Google ScholarDigital Library
28. Pauly, M., Keiser, R., Kobbelt, L. P., and Gross, M. 2003. Shape modeling with point-sampled geometry. ACM Transactions on Graphics (Proceedings of ACM SIGGRAPH 2003) 22, 3, 641–650.]] Google ScholarDigital Library
29. Pauly, M., Mitra, N., and Guibas, L. 2004. Uncertainty and variability in point cloud surface data. In Eurographics Symposium on Point-Based Graphics, 77–84.]] Google ScholarDigital Library
30. Rousseeuw, P., and Leroy, A. 1987. Robust Regression and Outlier Detection. John Wiley & Sons.]] Google ScholarDigital Library
31. Sinha, S. S., and Schunck, B. G. 1992. A two-stage algorithm for discontinuity-preserving surface reconstruction. IEEE Transactions on Pattern Analysis and Machine Intelligence 14, 1, 36–55.]] Google ScholarDigital Library
32. Stewart, C. V. 1999. Robust parameter estimation in computer vision. SIAM Review 41, 3, 513–537.]] Google ScholarDigital Library
33. Taubin, G. 1995. A signal processing approach to fair surface design. In ACM SIGGRAPH 1995, 351–358.]] Google ScholarDigital Library
34. Turk, G., and Levoy, M. 1994. Zippered polygon meshes from range images. In ACM SIGGRAPH 1994, 311–318.]] Google ScholarDigital Library
35. Varadhan, G., Krishnan, S., Kim, Y. J., and Manocha, D. 2003. Feature-sensitive subdivision and iso-surface reconstruction. In IEEE Visualization 2003, 99–106.]] Google ScholarDigital Library
36. Wheeler, M. D., Sato, Y., and Ikeuchi, K. 1998. Consensus surfaces for modeling 3D objects from multiple range images. In ICCV ’98, 917–924.]] Google ScholarDigital Library
37. Xie, H., Wang, J., Hua, J., Qin, H., and Kaufman, A. 2003. Piecewise g1 continuous surface reconstruction from noisy point cloud via local implicit quadric regression. In IEEE Visualization 2003, 259–266.]] Google ScholarDigital Library
38. Xie, H., McDonnell, K. T., and Qin, H. 2004. Surface reconstruction of noisy and defective data sets. In IEEE Visualization 2004, 259–266.]] Google ScholarDigital Library