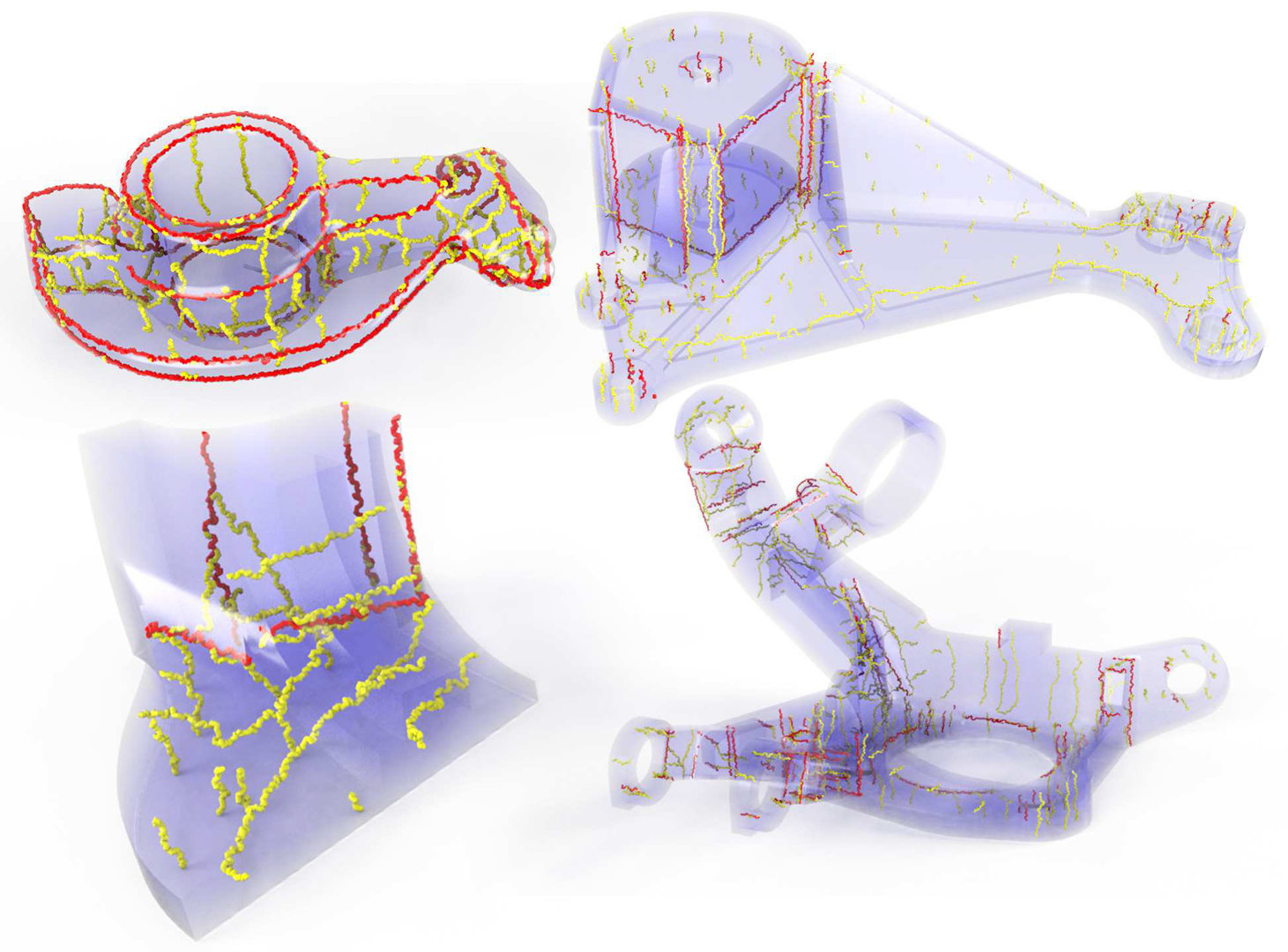
“Robust hex-dominant mesh generation using field-guided polyhedral agglomeration”
Conference:
Type(s):
Title:
- Robust hex-dominant mesh generation using field-guided polyhedral agglomeration
Session/Category Title: Meshing
Presenter(s)/Author(s):
Moderator(s):
Abstract:
We propose a robust and efficient field-aligned volumetric meshing algorithm that produces hex-dominant meshes, i.e. meshes that are predominantly composed of hexahedral elements while containing a small number of irregular polyhedra. The latter are placed according to the singularities of two optimized guiding fields, which allow our method to generate meshes with an exceptionally high amount of isotropy.The field design phase of our method relies on a compact quaternionic representation of volumetric octa-fields and a corresponding optimization that explicitly models the discrete matchings between neighboring elements. This optimization naturally supports alignment constraints and scales to very large datasets. We also propose a novel extraction technique that uses field-guided mesh simplification to convert the optimized fields into a hexdominant output mesh. Each simplification operation maintains topological validity as an invariant, ensuring manifold output. These steps easily generalize to other dimensions or representations, and we show how they can be an asset in existing 2D surface meshing techniques.Our method can automatically and robustly convert any tetrahedral mesh into an isotropic hex-dominant mesh and (with minor modifications) can also convert any triangle mesh into a corresponding isotropic quad-dominant mesh, preserving its genus, number of holes, and manifoldness. We demonstrate the benefits of our algorithm on a large collection of shapes provided in the supplemental material along with all generated results.
References:
1. 2016. AMPS. http://www.ampstech.com/ampstech/Asp/Solid.asp. (2016). Accessed: 2016-09-15.Google Scholar
2. 2016. ANSYSTurbogrid. http://www.ansys.com/Products/Fluids/ANSYS-TurboGrid/ANSYS-TurboGrid-Features#1. (2016). Accessed: 2016-09-15.Google Scholar
3. 2016. Apex. http://www.mscapex.com/apex-modeler/. (2016). Accessed: 2016-09-15.Google Scholar
4. 2016. Autodesk Simulation-Mechanical. http://www.autodesk.com/products/simulation-mechanical/features/all/gallery-view. (2016). Accessed: 2016-09-15.Google Scholar
5. 2016. BETA CAE. http://www.beta-cae.com/ansa.htm. (2016). Accessed: 2016-09-15.Google Scholar
6. 2016. Bolt. http://www.csimsoft.com/boltoverview. (2016). Accessed: 2016-09-03.Google Scholar
7. 2016. Cart3D. http://people.nas.nasa.gov/~aftosmis/cart3d/. (2016). Accessed: 2016-09-15.Google Scholar
8. 2016. CUBIT. http://cubit.sandia.gov/. (2016). Accessed: 2016-09-15.Google Scholar
9. 2016. Harpoon. http://www.sharc.co.uk/index.htm. (2016). Accessed: 2016-09-15.Google Scholar
10. 2016. Hexotic. https://www.rocq.inria.fr/gamma/gamma/Membres/CIPD/Loic.Marechal/Research/Hexotic.html. (2016). Accessed: 2016-09-15.Google Scholar
11. 2016. HEXPress. http://www.numeca.com/en/products/automeshtm/hexpresstm. (2016). Accessed: 2016-09-15.Google Scholar
12. 2016. HyperMesh. http://www.altairhyperworks.com/product/HyperMesh. (2016). Accessed: 2016-09-15.Google Scholar
13. 2016. Kubrix. http://www.itascacg.com/software/kubrix. (2016). Accessed: 2016-09-15.Google Scholar
14. 2016. LBIE. http://www.cs.utexas.edu/~bajaj/cvc/software/LBIE.shtml. (2016). Accessed: 2016-09-15.Google Scholar
15. 2016a. MeshGems. http://meshgems.com/volume-meshing-meshgems-hexa.html. (2016). Accessed: 2016-09-15.Google Scholar
16. 2016b. MeshGemsHybrid. http://meshgems.com/volume-meshing-meshgems-hybrid.html. (2016). Accessed: 2016-09-15.Google Scholar
17. 2016. PAMGEN. https://trilinos.org/packages/pamgen/. (2016). Accessed: 2016-09-15.Google Scholar
18. 2016. SiemenPLM. https://www.plm.automation.siemens.com/en_us/products/lms/virtual-lab/structures/meshing.shtml. (2016). Accessed: 2016-09-15.Google Scholar
19. 2016. TexMesher. http://texmesher.com/tex.html. (2016). Accessed: 2016-09-15.Google Scholar
20. 2016. Trelis. http://www.csimsoft.com/trelis.jsp. (2016). Accessed: 2016-09-15.Google Scholar
21. 2016. XBX. http://texmesher.com/kbx.html. (2016). Accessed: 2016-09-15.Google Scholar
22. Steven E. Benzley, Ernest Perry, Karl Merkley, Brett Clark, and Greg Sjaardema. 1995. A comparison of all hexagonal and all tetrahedral finite element meshes for elastic and elasto-plastic analysis. In In Proceedings, 4th International Meshing Roundtable. 179–191.Google Scholar
23. J.E. Bishop. 2014. A displacement-based finite element formulation for general polyhedra using harmonic shape functions. Internat. J. Numer. Methods Engrg. 97, 1 (2014), 1–31. Google ScholarCross Ref
24. David Bommes, Bruno Lévy, Nico Pietroni, Enrico Puppo, Claudio Silva, Marco Tarini, and Denis Zorin. 2013. Quad-Mesh Generation and Processing: A Survey. In Computer Graphics Forum, Vol. 32. Wiley Online Library, 51–76. Google ScholarDigital Library
25. David Bommes, Henrik Zimmer, and Leif Kobbelt. 2009. Mixed-integer Quadrangulation. ACM Trans. Graph. 28, 3 (July 2009), 77:1–77:10.Google ScholarDigital Library
26. M. Brewer, L. Diachin, P. Knupp, T. Leurent, and D. Melander. 2003. The Mesquite Mesh Quality Improvement Toolkit. In Proc. of the 12th International Meshing Roundtable. 239–250.Google Scholar
27. A. O. Cifuentes and A. Kalbag. 1992. A performance study of tetrahedral and hexahedral elements in 3-D finite element structural analysis. Finite Elements in Analysis and Design 12, 3–4 (1992), 313–318.Google ScholarDigital Library
28. Olga Diamanti, Amir Vaxman, Daniele Panozzo, and Olga Sorkine-Hornung. 2015. Integrable PolyVector Fields. ACM Transactions on Graphics (proceedings of ACM SIGGRAPH) 34, 4 (2015). Google ScholarDigital Library
29. Tor Dokken, Tom Lyche, and Kjell Fredrik Pettersen. 2013. Polynomial Splines over Locally Refined Box-partitions. Comput. Aided Geom. Des. 30, 3 (March 2013), 331–356. Google ScholarDigital Library
30. Randall Dougherty, Vance Faber, and Michael Murphy. 2004. Unflippable Tetrahedral Complexes. Discrete & Computational Geometry 32, 3 (2004), 309–315. Google ScholarDigital Library
31. Xianzhong Fang, Weiwei Xu, Hujun Bao, and Jin Huang. 2016. All-hex meshing using closed-form induced polycube. ACM Transactions on Graphics (TOG) 35, 4 (2016), 124.Google ScholarDigital Library
32. Xiaoming Fu, Chongyang Bai, and Yang Liu. 2016. Efficient Volumetric PolyCube-Map Construction. Computer Graphics Forum (Pacific Graphics) 35, 7 (2016). Google ScholarDigital Library
33. Carlotta Giannelli, Bert JüTtler, and Hendrik Speleers. 2012. THB-splines: The Truncated Basis for Hierarchical Splines. Comput. Aided Geom. Des. 29, 7 (Oct. 2012), 485–498. Google ScholarDigital Library
34. James Gregson, Alla Sheffer, and Eugene Zhang. 2011. All-Hex Mesh Generation via Volumetric PolyCube Deformation. CGF 30, 5 (2011), 1407–1416. Google ScholarCross Ref
35. Jin Huang, Tengfei Jiang, Zeyun Shi, Yiying Tong, Hujun Bao, and Mathieu Desbrun. 2014. L1-based Construction of Polycube Maps from Complex Shapes. ACM Trans. Graph. 33, 3 (2014), 25:1–25:11.Google ScholarDigital Library
36. Jin Huang, Yiying Tong, Hongyu Wei, and Hujun Bao. 2011. Boundary Aligned Smooth 3D Cross-frame Field. ACM Trans. Graph. 30, 6 (Dec. 2011), 143:1–143:8.Google ScholarDigital Library
37. Yasushi Ito, Alan M. Shih, and Bharat K. Soni. 2009. Octree-based reasonable-quality hexahedral mesh generation using a new set of refinement templates. Int. J. Numer. Meth. Engng 77 (2009), 1809–1833. Google ScholarCross Ref
38. Wenzel Jakob, Marco Tarini, Daniele Panozzo, and Olga Sorkine-Hornung. 2015. Instant Field-aligned Meshes. ACM Trans. Graph. 34, 6 (Oct. 2015), 189:1–189:15.Google ScholarDigital Library
39. Tengfei Jiang, Jin Huang, Yiying Tong Yuanzhen Wang, and Hujun Bao. 2014. Frame Field Singularity Correction for Automatic Hexahedralization. IEEE TVCG 20, 8 (Aug. 2014), 1189–1199.Google Scholar
40. Hongmei Kang, Jinlan Xu, Falai Chen, and Jiansong Deng. 2015. A New Basis for PHT-splines. Graph. Models 82, C (Nov. 2015), 149–159. Google ScholarDigital Library
41. Bo Li, Xin Li, Kexiang Wang, and Hong Qin. 2013. Surface Mesh to Volumetric Spline Conversion with Generalized Poly-cubes. IEEE TVCG 19, 9 (2013), 1539–1551.Google Scholar
42. Yufei Li, Yang Liu, Weiwei Xu, Wenping Wang, and Baining Guo. 2012. All-hex Meshing Using Singularity-restricted Field. ACM Trans. Graph. 31, 6 (Nov. 2012), 177:1–177:11.Google ScholarDigital Library
43. Marco Livesu, Alessandro Muntoni, Enrico Puppo, and Riccardo Scateni. 2016. Skeleton-driven Adaptive Hexahedral Meshing of Tubular Shapes. In Computer Graphics Forum, Vol. 35. Wiley Online Library, 237–246. Google ScholarDigital Library
44. Marco Livesu, Nicholas Vining, Alla Sheffer, James Gregson, and Riccardo Scateni. 2013. PolyCut: monotone graph-cuts for PolyCube base-complex construction. ACM Trans. Graph. 32, 6 (2013), 171. Google ScholarDigital Library
45. Max Lyon, David Bommes, and Leif Kobbelt. 2016. HexEx: Robust Hexahedral Mesh Extraction. ACM Trans. Graph. 35, 4, Article 123 (July 2016), 11 pages.Google ScholarDigital Library
46. Loïc Maréchal. 2009. Advances in octree-based all-hexahedral mesh generation: handling sharp features. In proceedings of the 18th International Meshing Roundtable. Springer, 65–84. Google ScholarCross Ref
47. Sebastian Martin, Peter Kaufmann, Mario Botsch, Martin Wicke, and Markus Gross. 2008. Polyhedral Finite Elements Using Harmonic Basis Functions. In Proceedings of the Symposium on Geometry Processing (SGP ’08). Eurographics Association, Aire-la-Ville, Switzerland, Switzerland, 1521–1529. Google ScholarCross Ref
48. Matthias Nieser, Ulrich Reitebuch, and Konrad Polthier. 2011. CubeCover- Parameterization of 3D Volumes. CGF 30, 5 (2011), 1397–1406. Google ScholarCross Ref
49. Steven J. Owen and Sunil Saigal. 2000. H-Morph: an indirect approach to advancing front hex meshing. Internat. J. Numer. Methods Engrg. 49, 1–2 (2000), 289–312.Google ScholarCross Ref
50. Nicolas Ray, Wan Chiu Li, Bruno Lévy, Alla Sheffer, and Pierre Alliez. 2006. Periodic Global Parameterization. ACM Trans. Graph. 25, 4 (Oct. 2006), 1460–1485. Google ScholarDigital Library
51. Nicolas Ray and Dmitry Sokolov. 2015. On Smooth 3D Frame Field Design. CoRR abs/1507.03351 (2015).Google Scholar
52. Nicolas Ray, Dmitry Sokolov, and Bruno Lévy. 2016. Practical 3D Frame Field Generation. ACM Trans. Graph. 35, 6, Article 233 (Nov. 2016), 9 pages.Google ScholarDigital Library
53. Maxence Reberol and Bruno Lévy. 2016. Low-order continuous finite element spaces on hybrid non-conforming hexahedral-tetrahedral meshes. CoRR abs/1605.02626 (2016). http://arxiv.org/abs/1605.02626Google Scholar
54. Thomas W. Sederberg, Jianmin Zheng, Almaz Bakenov, and Ahmad Nasri. 2003. T-splines and T-NURCCs. ACM Trans. Graph. 22, 3 (July 2003), 477–484. Google ScholarDigital Library
55. Jason F. Shepherd and Chris R. Johnson. 2008. Hexahedral Mesh Generation Constraints. Eng. with Comput. 24, 3 (June 2008), 195–213. Google ScholarDigital Library
56. Hang Si. 2015. TetGen, a Delaunay-Based Quality Tetrahedral Mesh Generator. ACM Trans. Math. Softw. 41, 2, Article 11 (Feb. 2015), 36 pages.Google ScholarDigital Library
57. Dmitry Sokolov, Nicolas Ray, Lionel Untereiner, and Bruno Lévy. 2016. Hexahedral-Dominant Meshing. ACM Trans. Graph. 35, 5 (June 2016), 157:1–157:23.Google ScholarDigital Library
58. Yi Su, KH Lee, and A Senthil Kumar. 2004. Automatic hexahedral mesh generation for multi-domain composite models using a hybrid projective grid-based method. Computer-Aided Design 36, 3 (2004), 203–215. Google ScholarCross Ref
59. Srinivas C. Tadepalli, Ahmet Erdemir, and Peter R. Cavanagh. 2010. A Comparison of the Performance of Hexahedral and Tetrahedral Elements in Finite Element Models of the Foot. In ASME 2010 Summer Bioengineering Conference, Parts A and B. Naples, Florida, USA. Google ScholarCross Ref
60. Amir Vaxman, Marcel Campen, Olga Diamanti, Daniele Panozzo, David Bommes, Klaus Hildebrandt, and Mirela Ben-Chen. 2016. Directional Field Synthesis, Design, and Processing. In Computer Graphics Forum, Vol. 35. Wiley Online Library, 545–572.Google Scholar
61. Soji Yamakawa and Kenji Shimada. 2003. Fully-automated hex-dominant mesh generation with directionality control via packing rectangular solid cells. Internat. J. Numer. Methods Engrg. 57, 15 (2003), 2099–2129. Google ScholarCross Ref
62. Hongmei Zhang, Guoqun Zhao, and Xinwu Ma. 2007. Adaptive generation of hexahedral element mesh using an improved grid-based method. Computer-Aided Design 39, 10 (2007), 914–928. Google ScholarCross Ref
63. Yongjie Zhang and Chandrajit Bajaj. 2006. Adaptive and quality quadrilateral/hexahedral meshing from volumetric data. Computer methods in applied mechanics and engineering 195, 9 (2006), 942–960. Google ScholarCross Ref
64. Y. J. Zhang, X. Liang, and Guoliang Xu. 2013. A robust 2-refinement algorithm in octree or rhombic dodecahedral tree based all-hexahedral mesh generation. Computer Methods in Applied Mechanics and Engineering 256 (2013), 88–100. Google ScholarCross Ref