“Revisiting the k-means algorithm for fast trajectory segmentation” by Leiva and Vidal

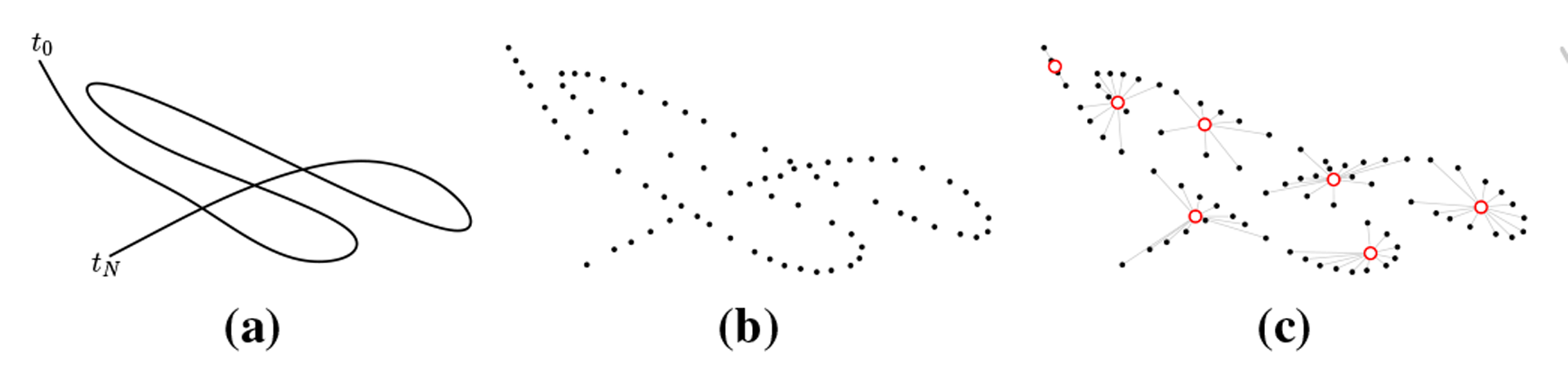
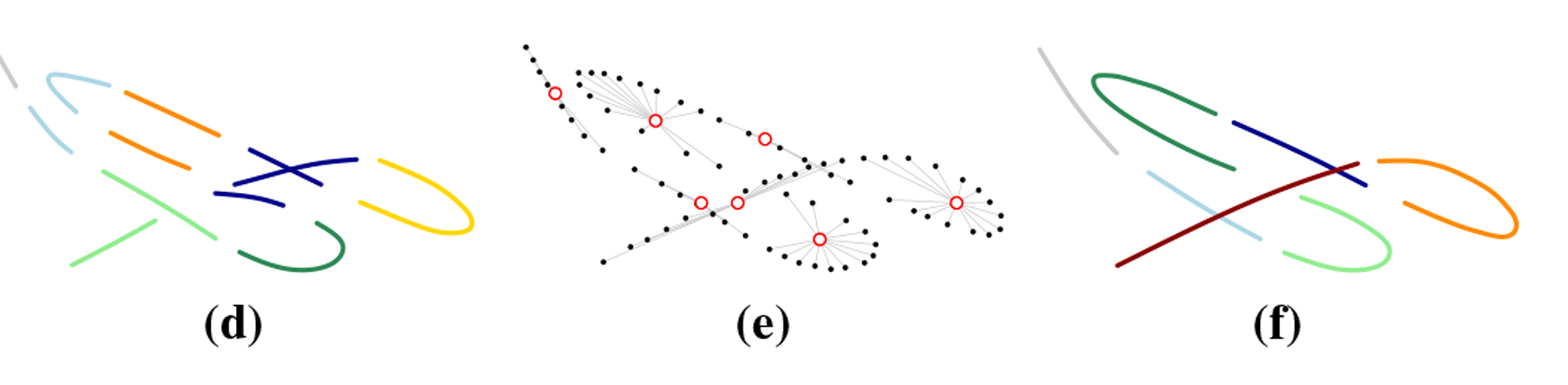
Many problems in Computer Science require a trajectory segmentation, in part due to the notably huge spectrum of devices that capture sequentially-generated information (e.g., motion sensors, video cameras, RFID tags, eye trackers, etc.) Segmentation leads to simplify the structure of the data, so that original objects can be divided into smaller, more compact structures. Seen this way, segmentation can be approached as a compression technique, i.e., organizing trajectories into segments whose members are similar in some way. This can be solved as a clustering problem. Unfortunately, to date we have not found a suitable method that can tap in a really simple way the temporal constraint implicitly embedded in the data. Moreover, near-optimal solutions such as kernel methods or hidden Markov models can be prohibitive if processing power is a restriction (e.g., on mobile devices).

1. Duda, R. O., Hart, P. E., and Stork, D. G. 2001. Pattern Classification, 2nd ed. John Wiley & Sons, ch. Unsupervised Learning and Clustering, 517–599.
2. Kuhn, M. H., Tomaschewski, H., and Ney, H. 1981. Fast nonlinear time alignment for isolated word recognition. In Proc. ICASSP, 736–740.
3. Lloyd, S. 1982. Least squares quantization in PCM. IEEE Trans. on Information Theory 28, 2, 129–137.