“Real-time robot motion planning using rasterizing computer graphics hardware” by Lengyel, Reichert, Donald and Greenberg
Conference:
Type(s):
Title:
- Real-time robot motion planning using rasterizing computer graphics hardware
Session/Category Title: Hardware
Presenter(s)/Author(s):
Moderator(s):
Abstract:
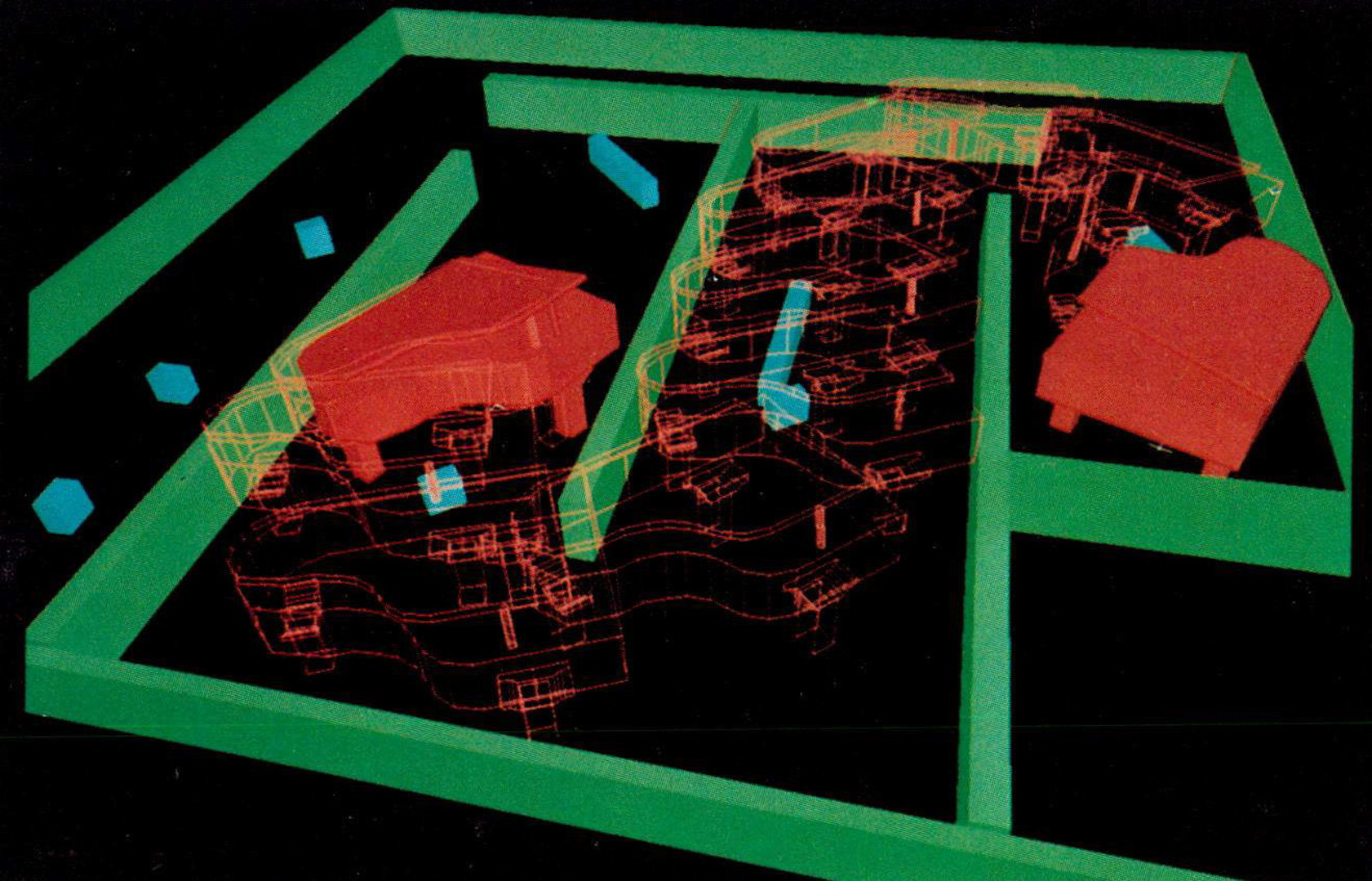
We present a real-time robot motion planner that is fast and complete to a resolution. The technique is guaranteed to find a path if one exists at the resolution, and all paths returned are safe. The planner can handle any polyhedral geometry of robot and obstacles, including disjoint and highly concave unions of polyhedra.The planner uses standard graphics hardware to rasterize configuration space obstacles into a series of bitmap slices, and then uses dynamic programming to create a navigation function (a discrete vector-valued function) and to calculate paths in this rasterized space. The motion paths which the planner produces are minimal with respect to an L1 (Manhattan) distance metric that includes rotation as well as translation.Several examples are shown illustrating the competence of the planner at generating planar rotational and translational plans for complex two and three dimensional robots. Dynamic motion sequences, including complicated and non-obvious backtracking solutions, can be executed in real time.
References:
1. Barraquand, J. and J. Latombe. Robot Motion Planning: A Distributed Representation Approach, Report No. STAN-CS-89-1257, Stanford University, Department of Computer Science, May 1989.
2. Canny, J., B. Donald, j. Reif, and P. Xavier. “On the Complexity of Kinodynamic Planning,” in 29th Symposium on the Foundations of Computer Science, White Plains NY., 1988.
3. Donald, B. R. Motion Planning with Six Degrees of Freedom, Report No. MIT AI-TR 791, MIT, Artificial Intelligence Laboratory, 1984.
4. Donald, B. R. “A Search Algorithm for Motion Planning with Six Degrees of Freedom,” Artificial Intelligence, 31, 1987, pages 295-353.
5. Dorst, L. and K. Trovato. “Optimal path planning by cost wave propagation in metric configuration space,” Proceedings of SPIE-The International Society for Optical Engineering, 1007, November 1988, pages 186- 197.
6. Donald, B. and P. Xavier. “A Provably Good Approximation Algorithm for Optimal-Time Trajectory Planning,” in IEEE Int. Conf. On Robotics and Automation, Scottsdale, AZ, 1989.
7. Donald, B. and P. Xavier. “Provably Good Approximation Algorithms for Optimal Kinodynamic Planning for Cartesian Robots and Open Chain Manipulators,” in Proceedings of the ACM Symposium on Computational Geometry, Berkeley, CA, 1990.
8. Khatib, O. and J. Le Maitre. “Dynamic Control of Manipulators Operating in a Complex Environment,” Proceedings Third International CISM-IFToMM Symposium, September 1978, pages 267-282.
9. Koditschek, D. E. “Exact Robot Navigation by Means of Potential Functions: Some Topological Considerations,” IEEE International Conference on Robotics and Automation, March 1987.
10. Koditschek, D. E. “Planning and Control via Potential Functions,” in Lozano-P6rez, T. and O. Khatib, editors, Robotics Review I, MIT Press, 1989, pages 349-367.
11. Lozano-P6rez, T. Spatial Planning: A Configuration Space Approach, A.I. Memo No. 605, Massachusetts Institute of Technology, Artificial Intelligence Laboratory, December 1980.
12. Lozano-P6rez, T. “Spatial Planning: A Configuration Space Approach,” IEEE Transactions on Computers, C-32, t983, pages 108-120.
13. Lozano-Pgrez, T. “A Simple Motion Planning Algorithm for General Robot Manipulator,” IEEE Journal of Robotics and Automation, RA-3(3), 1987, pages 224– 238.
14. Lozano-P6rez, T. and M. A. Wesley. “An Algorithm for Planning Collison-Free Paths Among Polyhedral Obstacles,” Communications of the ACM, 22, 1979, pages 560-570.
15. Pavlidis, T. “Contour Filling in Raster Graphics,” Proceedings of SIGGRAPH’81 (Dallas, Texas, August 3-7, 1981), 1981, pages 29-36.
16. Udupa, S. Collision Detection and Avoidance in Computer Controlled Manipulators, PhD dissertation, Department of Electrical Engineering, California Institute of Technology, Pasadena, California, 1977.
17. Yap, C. K. “Algorithmic Motion Planning,” in Schwartz, J. T. and C. K. Yap, editors, Advances in Robotics, Lawrence Erlbaum Associates, 1985.