“Re-usable Implicit Functions”
Conference:
Type(s):
Title:
- Re-usable Implicit Functions
Presenter(s)/Author(s):
Abstract:
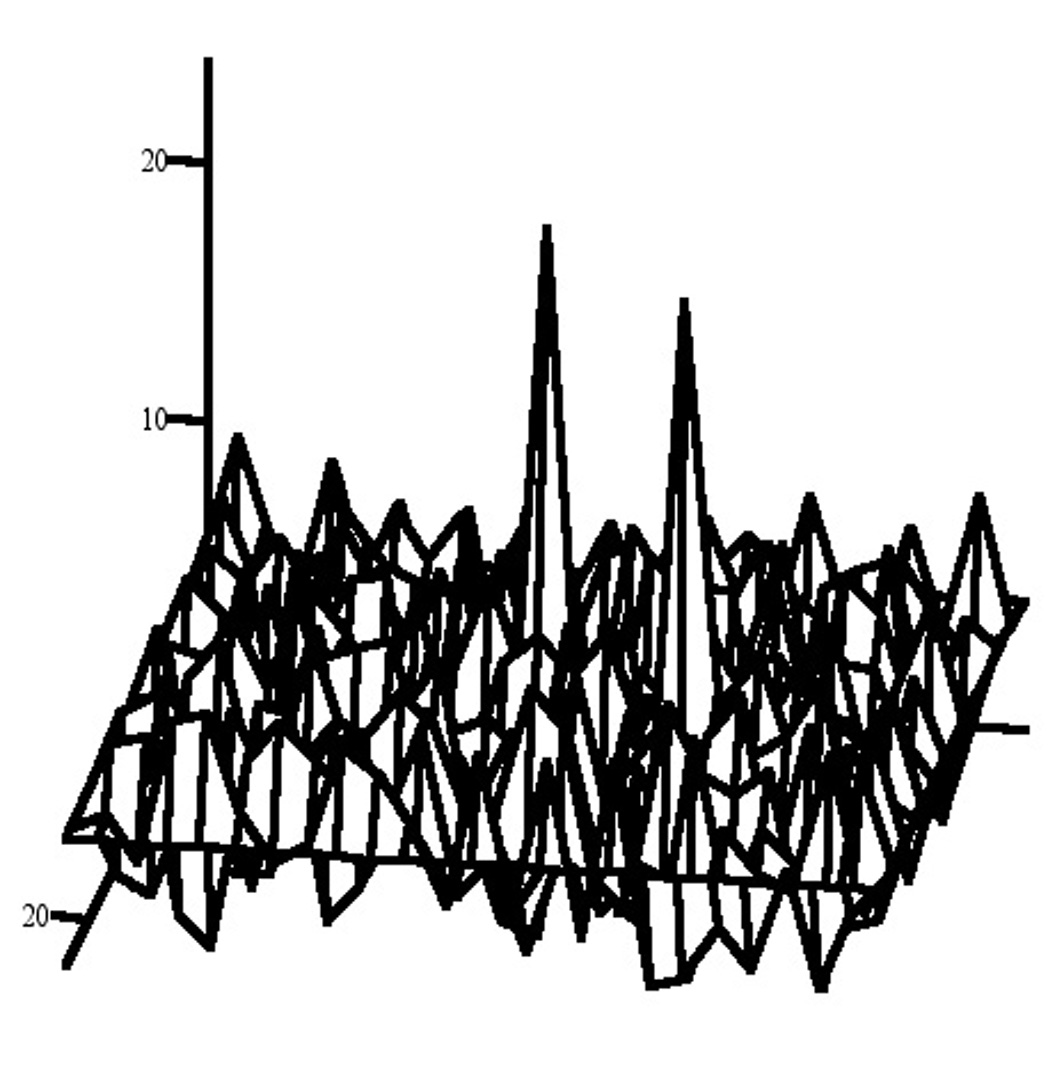
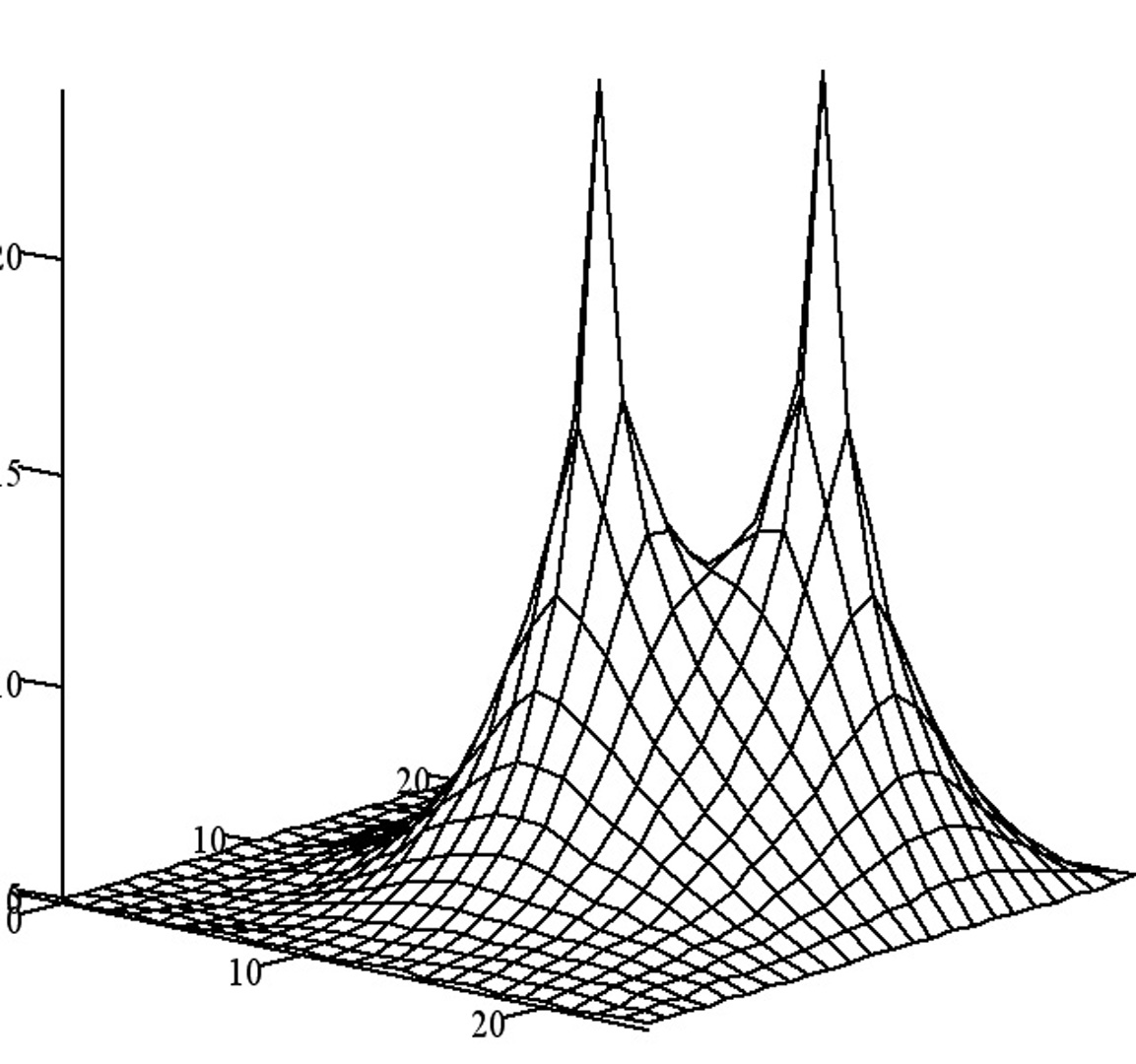
Implicit functions play a major role in modeling shapes. [Bloo] lists many implicit models such as super-quadrics, blended surfaces, convolution surfaces, metaballs, alpha patches and others. The zero-set of an implicit function f (where f(x) = 0) is typically the set of points employed as the model. The non-zero set is, however, also important as many operations on implicit models depend on the non-zero part. Operations on implicit models such as booleans, blending, shape texturing, or local parameterizations rely on smoothly varying space in the non-zero region to produce reasonable results. Many of the operations tend to degrade the space: thus booleans and blending create non-differentiabilities [Rock]. Some implicit functions like the Weierstrass function (a fractal) begin with undesirable characteristics. We present a method that redefines the non-zero space, without affecting the zero set; thus making operations more successful. It makes implicit modeling operations reusable and in some cases makes difficult implicit models usable.
References:
{Bloo} Bloomenthal, J., Introduction to Implicit Surfaces, Morgan Kaufmann Publishers, 1997.
{Rock} Rockwood, A., “The Displacement Method for Blending Surfaces in Solid Modeling,” ACM Transactions on Graphics, Special Issue on CAD/CAM, v.8, No.4, Oct. 1989, pp. 279–292.