“Qualitative organization of collections of shapes via quartet analysis” by Huang, Shamir, Shen, Zhang, Sheffer, et al. …

  • ©Shi-Sheng Huang, Ariel Shamir, Chao-Hui Shen, Hao Zhang, Alla Sheffer, Shi-Min Hu, and Daniel Cohen-Or

Conference:


Type(s):


Title:

    Qualitative organization of collections of shapes via quartet analysis

Session/Category Title:   Shape Analysis

Presenter(s)/Author(s):


Moderator(s):


Abstract:


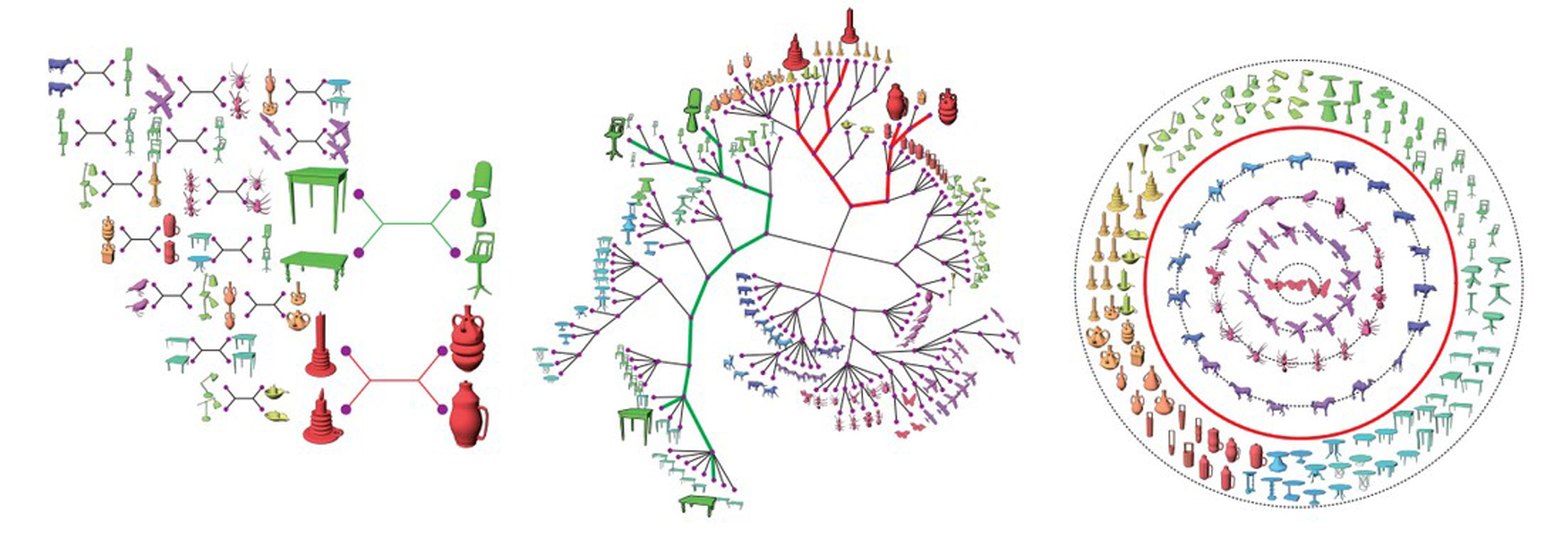
    We present a method for organizing a heterogeneous collection of 3D shapes for overview and exploration. Instead of relying on quantitative distances, which may become unreliable between dissimilar shapes, we introduce a qualitative analysis which utilizes multiple distance measures but only in cases where the measures can be reliably compared. Our analysis is based on the notion of quartets, each defined by two pairs of shapes, where the shapes in each pair are close to each other, but far apart from the shapes in the other pair. Combining the information from many quartets computed across a shape collection using several distance measures, we create a hierarchical structure we call categorization tree of the shape collection. This tree satisfies the topological (qualitative) constraints imposed by the quartets creating an effective organization of the shapes. We present categorization trees computed on various collections of shapes and compare them to ground truth data from human categorization. We further introduce the concept of degree of separation chart for every shape in the collection and show the effectiveness of using it for interactive shapes exploration.

References:


    1. Bronstein, A. M., Bronstein, M. M., Kimmel, R., Mahmoudi, M., and Sapiro, G. 2010. A gromov-hausdorff framework with diffusion geometry for topologically-robust non-rigid shape matching. Int. J. Comput. Vision 89, 2-3, 266–286. Google ScholarDigital Library
    2. Bronstein, A. M., Bronstein, M. M., Guibas, L. J., and Ovsjanikov, M. 2011. Shape google: Geometric words and expressions for invariant shape retrieval. ACM Trans. Graph. 30, 1, 1:1–1:20. Google ScholarDigital Library
    3. Chen, D.-Y., Tian, X.-P., Shen, Y.-T., and Ouhyoung, M. 2003. On visual similarity based 3D model retrieval. Comput. Graph. Forum 22, 3, 223–232.Google ScholarCross Ref
    4. Dueck, D., and Frey, B. J. 2007. Non-metric affinity propagation for unsupervised image categorization. In IEEE 11th International Conference on Computer Vision, IEEE, 1–8.Google Scholar
    5. Dumais, S., and Chen, H. 2000. Hierarchical classification of web content. In Proc. of ACM SIGIR conference on Research and development in information retrieval, 256–263. Google ScholarDigital Library
    6. Erdos, P. L., Steel, M. A., Szekely, L. A., and Warnow, T. J. 1997. A few logs suffice to build (almost) all trees (ii). Tech. rep. Google ScholarDigital Library
    7. Everitt, B. S., Landau, S., Leese, M., and Stahl, D. 2011. Cluster analysis, 5th edition. Wiley Series in Probability and Statistics.Google Scholar
    8. Frey, B. J., and Dueck, D. 2007. Clustering by passing messages between data points. Science 315, 972–976.Google ScholarCross Ref
    9. Gal, R., Shamir, A., and Cohen-Or, D. 2007. Pose-oblivious shape signature. IEEE Transactions on Visualization and Computer Graphics 13, 2, 261–271. Google ScholarDigital Library
    10. Golovinskiy, A., and Funkhouser, T. 2009. Consistent segmentation of 3D models. Comput. Graph. 33, 3, 262–269. Google ScholarDigital Library
    11. Kazhdan, M., Funkhouser, T., and Rusinkiewicz, S. 2003. Rotation invariant spherical harmonic representation of 3d shape descriptors. In SGP’03, 156–164. Google ScholarDigital Library
    12. Kazhdan, M., Funkhouser, T., and Rusinkiewicz, S. 2003. Rotation invariant spherical harmonic representation of 3d shape descriptors. In Proceedings of the 2003 Eurographics/ACM SIGGRAPH symposium on Geometry processing, Eurographics Association, Aire-la-Ville, Switzerland, Switzerland, SGP ’03, 156–164. Google ScholarDigital Library
    13. Kim, V. G., Li, W., Mitra, N. J., DiVerdi, S., and Funkhouser, T. 2012. Exploring collections of 3D models using fuzzy correspondences. ACM Trans. Graph. 31, 4, 54:1–54:11. Google ScholarDigital Library
    14. Kohonen, T. 1982. Self-organized formation of topologically correct feature maps. Biological Cybernetics 43, 59–69.Google ScholarCross Ref
    15. Ling, H., and Jacobs, D. W. 2007. Shape classification using the inner-distance. IEEE Trans. Pattern Anal. Mach. Intell. 29, 2, 286–299. Google ScholarDigital Library
    16. Mardia, K. V., Kent, J. T., and Bibby, J. M. 1980. Multivariate Analysis (Probability And Mathematical Statistics) Author:, Publisher. Academic Press.Google Scholar
    17. Osada, R., Funkhouser, T., Chazelle, B., and Dobkin, D. 2002. Shape distributions. ACM Trans. Graph. 21, 4, 807–832. Google ScholarDigital Library
    18. Ovsjanikov, M., Li, W., Guibas, L., and Mitra, N. J. 2011. Exploration of continuous variability in collections of 3D shapes. ACM Trans. Graph. 30, 4, 33:1–33:10. Google ScholarDigital Library
    19. Ranwez, V., and Gascuel, O. 2001. Quartet-based phylogenetic inference: Improvements and limits. Molecular Biology and Evolution 18, 6, 1103–1116.Google ScholarCross Ref
    20. Semple, C., and Steel, M. 2003. Phylogenetics. Oxford Univerity Press.Google Scholar
    21. Shapira, L., Shamir, A., and Cohen-Or, D. 2008. Consistent mesh partitioning and skeletonisation using the shape diameter function. Vis. Comput. 24, 4, 249–259. Google ScholarDigital Library
    22. Shilane, P., Min, P., Kazhdan, M., and Funkhouser, T. 2004. The princeton shape benchmark. In SMI’04, 167–178. Google ScholarDigital Library
    23. Sidi, O., van Kaick, O., Kleiman, Y., Zhang, H., and Cohen-Or, D. 2011. Unsupervised co-segmentation of a set of shapes via descriptor-space spectral clustering. ACM Trans. Graph. 30, 6, 126:1–126:10. Google ScholarDigital Library
    24. Snir, S., and Rao, S. 2010. Quartets maxcut: A divide and conquer quartets algorithm. IEEE/ACM Trans. Comput. Biol. Bioinformatics 7, 4, 704–718. Google ScholarDigital Library
    25. Strimmer, K., Goldman, N., and von Haeseler, A. 1997. Bayesian probabilites and quartet puzzling. Molecular Biology and Evolution. 14, 2, 210–211.Google ScholarCross Ref
    26. Tangelder, J. W., and Veltkamp, R. C. 2008. A survey of content based 3D shape retrieval methods. Multimedia Tools Appl. 39, 3, 441–471. Google ScholarDigital Library
    27. Wang, Y., Asafi, S., van Kaick, O., Zhang, H., Cohen-Or, D., and Chen, B. 2012. Active co-analysis of a set of shapes. ACM Trans. Graph. 31, 6 (Nov.), 165:1–165:10. Google ScholarDigital Library
    28. Weigend, A. S., Wiener, E. D., and Pedersen, J. O. 1999. Exploiting hierarchy in text categorization. Information Retrieval 1, 3 (Oct.), 193–216. Google ScholarDigital Library
    29. Willson, S. J. 1998. Building phylogenetic trees from quartets by using local inconsistency measures. Molecular Biology and Evolution 16, 5, 685–693.Google ScholarCross Ref
    30. Xu, K., Li, H., Zhang, H., Cohen-Or, D., Xiong, Y., and Cheng, Z.-Q. 2010. Style-content separation by anisotropic part scales. ACM Trans. Graph. 29, 6 (Dec.), 184:1–184:10. Google ScholarDigital Library

ACM Digital Library Publication:


Overview Page: