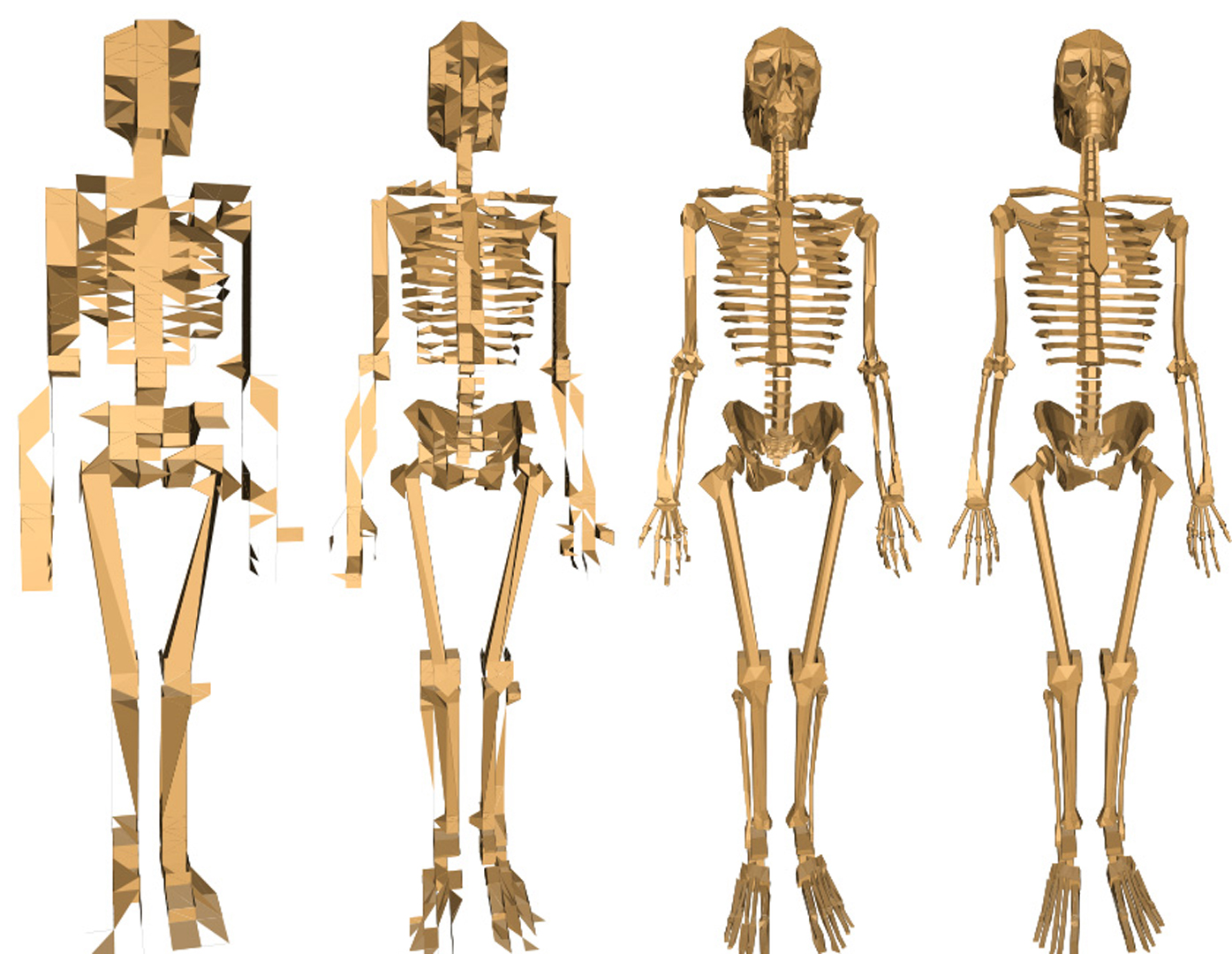
“Progressive lossless compression of arbitrary simplicial complexes”

Efficient algorithms for compressing geometric data have been widely developed in the recent years, but they are mainly designed for closed polyhedral surfaces which are manifold or “nearly manifold”. We propose here a progressive geometry compression scheme which can handle manifold models as well as “triangle soups” and 3D tetrahedral meshes. The method is lossless when the decompression is complete which is extremely important in some domains such as medical or finite element.While most existing methods enumerate the vertices of the mesh in an order depending on the connectivity, we use a kd-tree technique [Devillers and Gandoin 2000] which does not depend on the connectivity. Then we compute a compatible sequence of meshes which can be encoded using edge expansion [Hoppe et al. 1993] and vertex split [Popović and Hoppe 1997].The main contributions of this paper are: the idea of using the kd-tree encoding of the geometry to drive the construction of a sequence of meshes, an improved coding of the edge expansion and vertex split since the vertices to split are implicitly defined, a prediction scheme which reduces the code for simplices incident to the split vertex, and a new generalization of the edge expansion operation to tetrahedral meshes.

1. ALLIEZ, P., AND DESBRUN, M. 2001. Progressive compression for lossless transmission of triangle meshes. In SIGGRAPH 2001 Conference Proc., 199-202. Google Scholar
2. ALLIEZ, P., AND DESBRUN, M. 2001. Valence-driven connectivity encoding for 3d meshes. In Eurographics 2001 Conference Proc., 480-489.Google Scholar
3. BAJAJ, C., CUTCHIN, S., PASCUCCI, V., AND ZHUANG, G. 1999. Error resilient streaming of compressed vrml. Tech. rep., University of Texas.Google Scholar
4. BAJAJ, C., PASCUCCI, V., AND ZHUANG, G. 1999. Progressive compression and transmission of arbitrary triangular meshes. In IEEE Visualization 99 Conference Proc., 307-316. Google Scholar
5. BAJAJ, C., PASCUCCI, V., AND ZHUANG, G. 1999. Single resolution compression of arbitrary triangular meshes with properties. Computational Geometry: Theory and Applications, 247-296. Google Scholar
6. COHEN-OR, D., LEVIN, D., AND REMEZ, O. 1999. Progressive compression of arbitrary triangular meshes. In IEEE Visualization 99 Conference Proc., 67-72. Google Scholar
7. DEERING, M. 1995. Geometry compression. In SIGGRAPH 95 Conference Proc., 13-20. Google Scholar
8. DEVILLERS, O., AND GANDOIN, P.-M. 2000. Geometric compression for interactive transmission. In IEEE Visualization 2000 Conference Proc., 319-326. Google Scholar
9. EVANS, F., SKIENA, S., AND VARSHNEY, A. 1996, Optimizing triangle strips for fast rendering. In IEEE Visualization 96 Conference Proc., 319-326. Google Scholar
10. GUÉZIEC, A., BOSSEN, F., TAUBIN, G., AND SILVA, C. 1999. Efficient compression of non-manifold polygonal meshes. Comput. Geom. Theory Appl. 14, 137-166. Google Scholar
11. GUMHOLD, S., AND STRASSER, W. 1998. Real time compression of triangle mesh connectivity. In SIGGRAPH 98 Conference Proc., 133-140. Google Scholar
12. GUMHOLD, S., GUTHE, S., AND STRASSER, W. 1999. Tetrahedral mesh compression with the cut-border machine. In IEEE Visualization 99 Conference Proc., 91-98. Google Scholar
13. HECKBERT, P. S., AND GARLAND, M. 1997. Survey of polygonal surface simplification algorithms. Tech. rep., Carnegie Mellon University. Google Scholar
14. HOPPE, H., DEROSE, T., DUCHAMP, T., MCDONALD, J., AND STUETZLE, W. 1993. Mesh optimization. In SIGGRAPH 93 Conference Proc., 1 9-26. Google Scholar
15. ISENBURG, M., AND SNOEYINK, J. 1999. Mesh collapse compression. In Symposium on Computational Geometry, 419-420. Google Scholar
16. ISENBURG, M. 2000. Triangle fix er: Edge-based connectivity encoding. In 16th European Workshop on Computational Geometry Proc. Google Scholar
17. KARNI, Z., AND GOTSMAN, C. 2000. Spectral compression of mesh geometry. In SIGGRAPH 2000 Conference Proc., 279-286. Google Scholar
18. KHODAKOVSKY, A., SCHRÖDER, P., AND SWELDENS, W. 2000. Progressive geometry compression. In SIGGRAPH 2000 Conference Proc., 271-278. Google Scholar
19. KING, D., AND ROSSIGNAC, J. 1999. Guaranteed 3.67v bit encoding of planar triangle graphs. In Canadian Conference on Computational Geometry Proc., 146-149.Google Scholar
20. LI, J., AND KUO, C.-C. J. 1998. A dual graph approach to 3d triangular mesh compression. In IEEE International Conference on Image Processing Proc.Google Scholar
21. PAJAROLA, R., AND ROSSIGNAC, J. 2000. Compressed progressive meshes. IEEE Transactions on Visualization and Computer Graphics 6, 1 (January-March), 79-93. Google Scholar
22. PAJAROLA, R., AND ROSSIGNAC, J. 2000. Squeeze: Fast and progressive decompression of triangle meshes. CGI 2000 Proc., 173-182. Google Scholar
23. PAJAROLA, R., ROSSIGNAC, J., AND SZYMCZAK, A. 1999. Implant sprays: Compression of progressive tetrahedral mesh connectivity. In IEEE Visualization 99 Conference Proc., 299-306. Google Scholar
24. POPOVIĆ, J.,., AND HOPPE, H. 1997. Progressive simplicial complexes. In SIGGRAPH 97 Conference Proc., 217-224. Google Scholar
25. ROSSIGNAC, J., AND BORREL, P. 1993, Geometric Modeling in Computer Graphics. Springer-Verlag, July, ch. Multi-Resolution 3D Approximations for Rendering Complex Scenes, 455-465.Google Scholar
26. ROSSIGNAC, J., AND SZYMCZAK, A. 1999. Wrap&zip: Linear decoding of planar triangle graphs. Computational Geometry: Theory and Applications, 119-135. Google Scholar
27. ROSSIGNAC, J. 1999. Edgebreaker: Connectivity compression for triangle meshes. IEEE Transactions on Visualization and Computer Graphics, 47-61. Google Scholar
28. SCHMALSTIEG, D., AND SCHAUFLER, G. 1997. Smooth levels of detail. In IEEE Virtual Reality Annual International Symposium, 12-19. Google Scholar
29. TAUBIN, G., AND ROSSIGNAC, J. 1998. Geometric compression through topological surgery. ACM Transactions on Graphics 17, 2, 84-115. Google Scholar
30. TAUBIN, G., GUÉZIEC, A., HORN, W., AND LAZARUS, F. 1998. Progressive forest split compression. In SIGGRAPH 98 Conference Proc., 123-132. Google Scholar
31. TOUMA, C., AND GOTSMAN, C. 1998. Triangle mesh compression. In Graphics Interface 98 Conference Proc., 26-34,Google Scholar
32. WITTEN, I., NEAL, R., AND CLEARY, J. 1987. Arithmetic coding for data compression. Communications of the ACM 30, 6, 520-540. Google Scholar
33. YANG, C., MITRA, T., AND CHIUEH, T. 2000. On-the-fly rendering of losslessly compressed irregular volume data. In 11th IEEE Visualization Conference, 329-336. Google Scholar