“Potential Fields and Implicit Modeling” by Tankelevich and Rockwood
Conference:
Type(s):
Entry Number: 003
Title:
- Potential Fields and Implicit Modeling
Presenter(s)/Author(s):
Abstract:
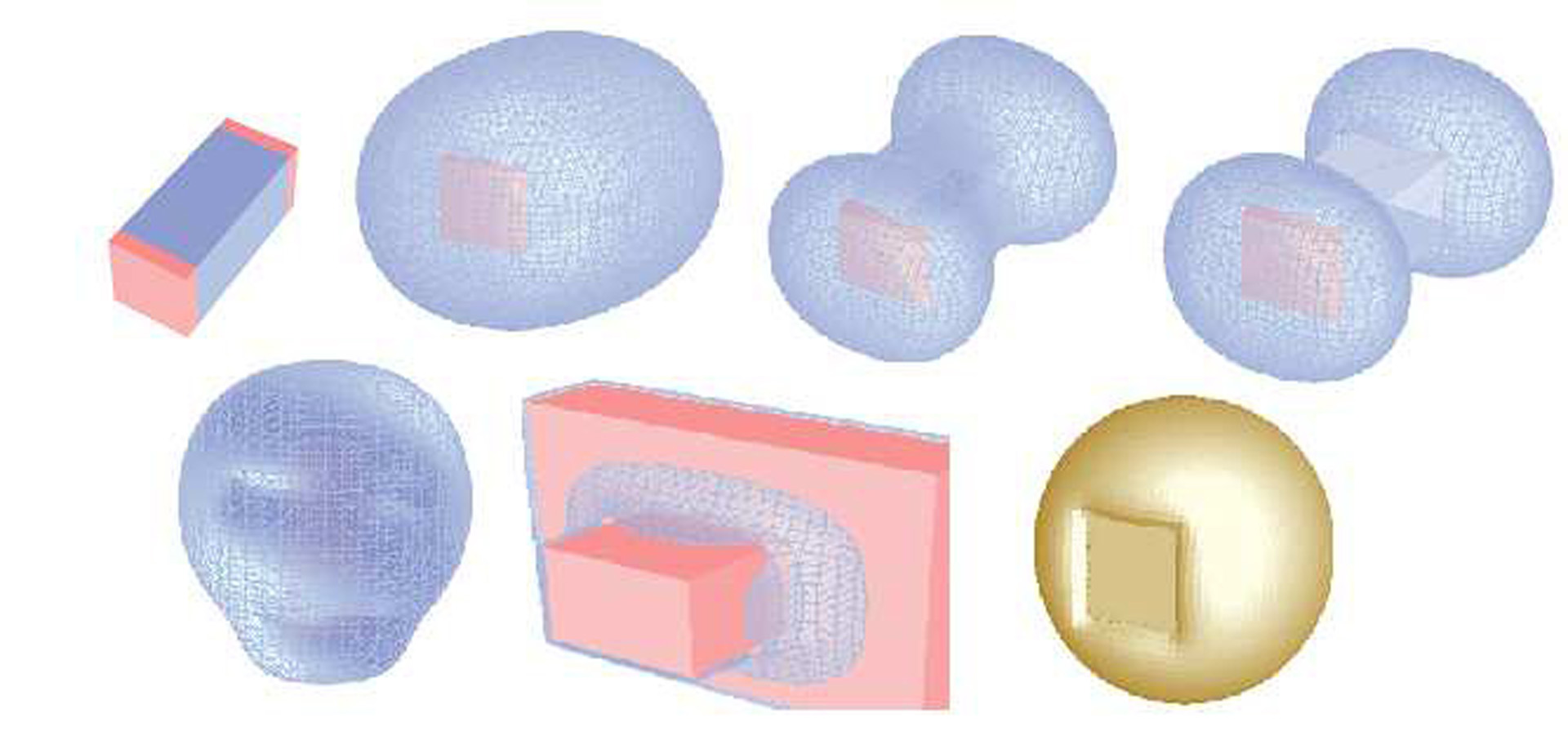
A new method of geometric modeling based on potential fields devised as a solution of an external Dirichlet problem for the Laplace equation is presented. The PF method belongs to class of implicit modeling techniques, such as level sets and distance fields, and has an advantage of using smooth streamlines converging to threshold surfaces. We consider two different tasks with respect to the potential fields:
(a) definition of solid models, and
(b) proximity solutions applied to blending, texturing, offsetting, collision control, and other practical problems. This study concerns both general computer graphics area and the needs of computer-added design in manufacturing. Two modeling approaches come close to our method:
(a) convolution of skeletons [BLOO], and
(b) blobby objects [BLIN] (to a lesser degree).
We propose to use a Dirichlet problem’s solution to obtain a more generalized definition of implicit surfaces. In this case, the implicit surface is generated as an equipotential solution of the Laplace equation with given boundary conditions which is essentially equivalent to using the double layer potential to generate an isosurface.
References:
1. {Bloo} Bloomenthal, J., Introduction to Implicit Surfaces, Morgan Kaufmann Publishers, 1997.
2. {Blin} Blinn, J., A Generalization of Algebraic Surface Drawing, ACM Transactions on Graphics, Vol. 1, No. 3, pp. 235–256, July, 1982.