“PolyMerge: a fast approach for hex-dominant mesh generation” by Sánchez and Fels
Conference:
Type(s):
Entry Number: 81
Title:
- PolyMerge: a fast approach for hex-dominant mesh generation
Presenter(s)/Author(s):
Abstract:
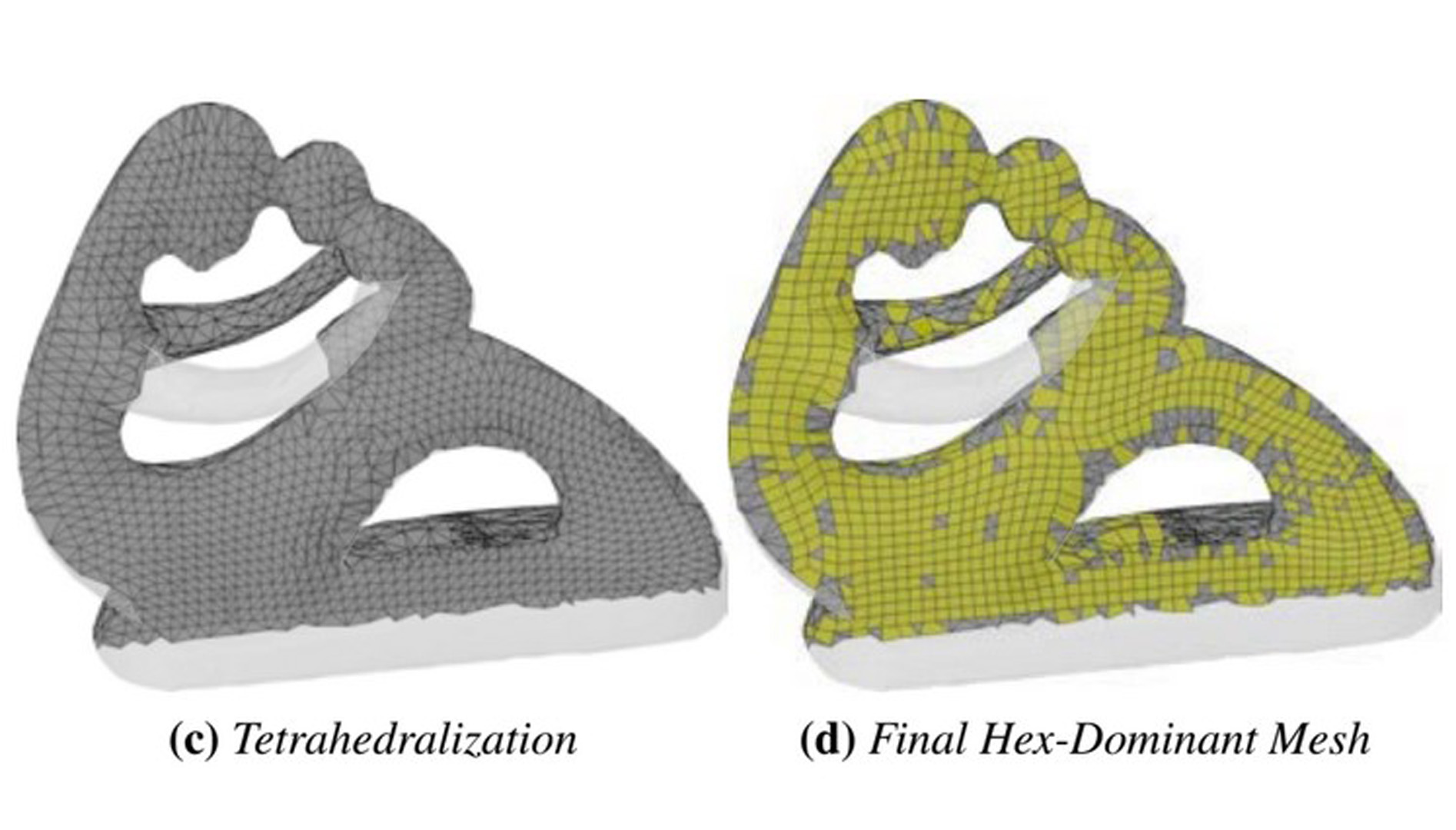
Hex-dominant meshes are often preferred for finite element simulations due to their superior convergence properties and lack of numerical artifacts (e.g. locking). Unfortunately, constructing such meshes for arbitrary shapes is still a challenging task. One recent approach is to use a low-distortion map between a target shape and its nearest PolyCube form (union of rectangular prisms) [Livesu et al. 2013]. A hex mesh can be constructed quite easily in the deformed space, then transformed back to the original coordinate system. However, the distortion may be quite large, leading to poorly-conditioned elements (highly stretched/skewed). Another option to is to create an initial tetrahedral mesh, then convert this to a hex-dominant one by merging groups of tetrahedra. In [Yamakawa and Shimada 2003], a graph search is used to identify potential tet groupings that can be merged to form hex elements. Finding hexes this way leads to a combinatorial problem, which is computationally expensive. It also suffers from redundant searches, checking the same patterns of tets multiple times.
We present a new hex-meshing strategy that addresses these deficiencies. Our tet-merging algorithm is up to 40 faster than the current state-of-the-art, allowing us to generate hex-dominant meshes (80% by volume) with more than 100k elements in less than one minute.
References:
- Livesu, M., Vining, N., Sheffer, A., Gregson, J., and Scateni, R. 2013. Polycut: Monotone graph-cuts for polycube base-complex construction. ACM Trans. Graph. 32, 6 (Nov.), 171:1–171:12.
- Yamakawa, S., and Shimada, K. 2003. Fully-automated hex-dominant mesh generation with directionality control via packing rectangular solid cells. Int. J. for Num. Meth. in Eng. (IJNME) 57, 15, 2099–2129.