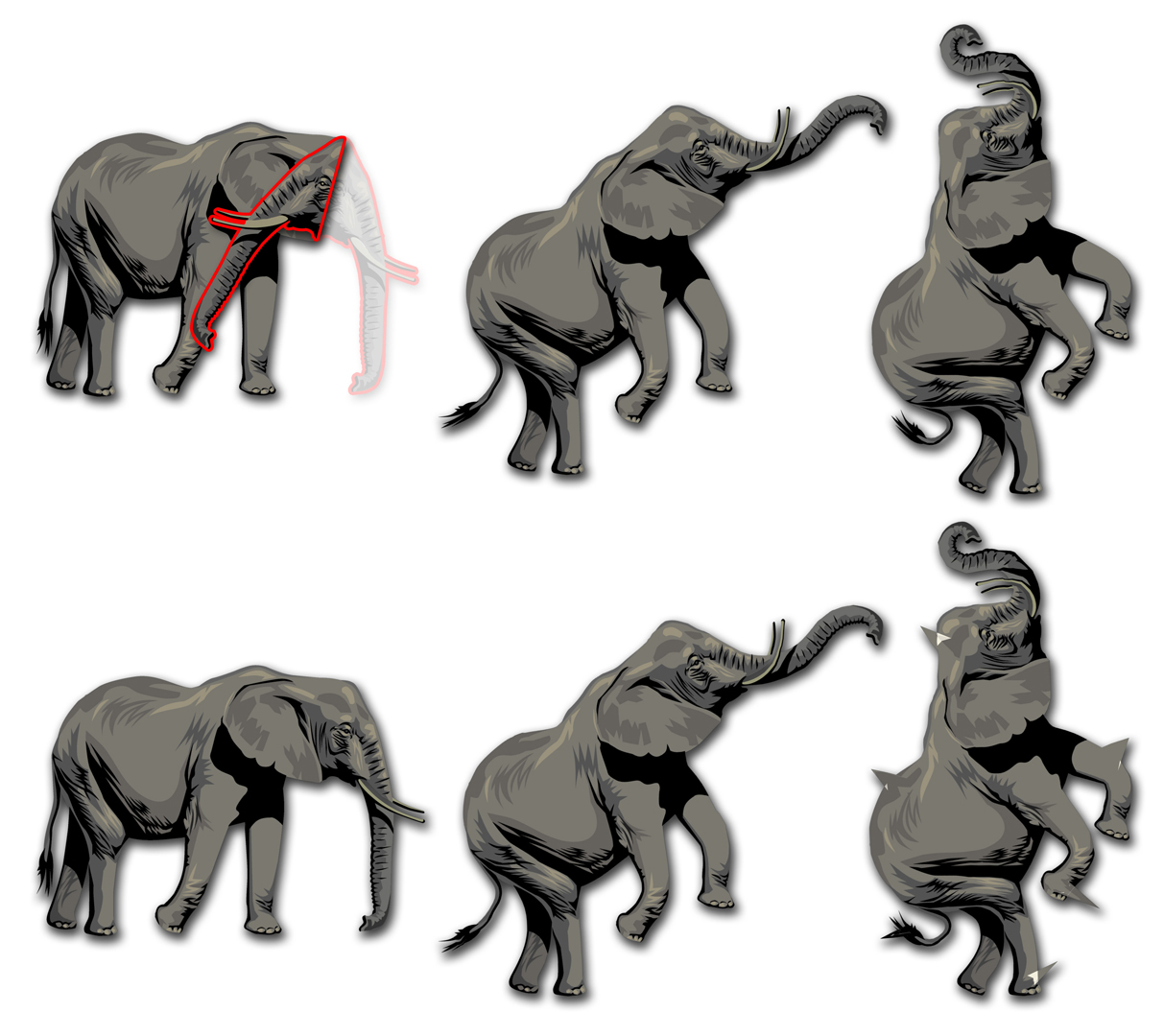
“Planar shape interpolation with bounded distortion” by Chen, Weber, Keren and Ben-Chen
Conference:
Type(s):
Title:
- Planar shape interpolation with bounded distortion
Session/Category Title: Deformation & Distortion
Presenter(s)/Author(s):
Moderator(s):
Abstract:
Planar shape interpolation is widely used in computer graphics applications. Despite a wealth of interpolation methods, there is currently no approach that produces shapes with a bounded amount of distortion with respect to the input. As a result, existing interpolation methods may produce shapes that are significantly different than the input and can suffer from fold-overs and other visual artifacts, making them less useful in many practical scenarios. We introduce a novel shape interpolation scheme designed specifically to produce results with a bounded amount of conformal (angular) distortion. Our method is based on an elegant continuous mathematical formulation and provides several appealing properties such as existence and uniqueness of the solution as well as smoothness in space and time domains. We further present a discretization and an efficient practical algorithm to compute the interpolant and demonstrate its usability and good convergence behavior on a wide variety of input shapes. The method is simple to implement and understand. We compare our method to state-of-the-art interpolation methods and demonstrate its superiority in various cases.
References:
1. Alexa, M., Cohen-Or, D., and Levin, D. 2000. As-rigid-as-possible shape interpolation. In Proceedings of the 27th annual conference on Computer graphics and interactive techniques, ACM Press/Addison-Wesley Publishing Co., 157–164. Google ScholarDigital Library
2. Alexa, M. 2002. Recent advances in mesh morphing. In Computer graphics forum, vol. 21, Wiley Online Library, 173–198.Google Scholar
3. Bao, Y., Guo, X., and Qin, H. 2005. Physically based morphing of point-sampled surfaces. Computer Animation and Virtual Worlds 16, 3–4, 509–518. Google ScholarDigital Library
4. Baxter, W., Barla, P., and Anjyo, K. 2008. Rigid shape interpolation using normal equations. In Proceedings of the 6th international symposium on Non-photorealistic animation and rendering, ACM, 59–64. Google ScholarDigital Library
5. Chao, I., Pinkall, U., Sanan, P., and Schröder, P. 2010. A simple geometric model for elastic deformations. ACM Transactions on Graphics (TOG) 29, 4, 38. Google ScholarDigital Library
6. Choi, J., and Szymczak, A. 2003. On coherent rotation angles for as-rigid-as-possible shape interpolation.Google Scholar
7. Crane, K., Pinkall, U., and Schröder, P. 2011. Spin transformations of discrete surfaces. ACM Trans. Graph. 40. Google ScholarDigital Library
8. Fröhlich, S., and Botsch, M. 2011. Example-driven deformations based on discrete shells. In Computer Graphics Forum, vol. 30, Wiley Online Library, 2246–2257.Google Scholar
9. Fu, H., Tai, C., and Au, O. 2005. Morphing with laplacian coordinates and spatial-temporal texture. In Proceedings of Pacific Graphics, 100–102.Google Scholar
10. Gray, A., Abbena, E., and Salamon, S. 2006. Modern differential geometry of curves and surfaces with Mathematica. Chapman & Hall/CRC. Google ScholarDigital Library
11. Gu, D., Luo, F., and Yau, S. 2010. Fundamentals of computational conformal geometry. Mathematics in Computer Science 4, 4, 389–429.Google ScholarCross Ref
12. Hu, S., Li, C., and Zhang, H. 2004. Actual morphing: a physics-based approach to blending. In Proceedings of the ninth ACM symposium on Solid modeling and applications, Eurographics Association, 309–314. Google ScholarDigital Library
13. Igarashi, T., Moscovich, T., and Hughes, J. 2005. As-rigid-as-possible shape manipulation. In ACM Transactions on Graphics (TOG), vol. 24, ACM, 1134–1141. Google ScholarDigital Library
14. Kilian, M., Mitra, N., and Pottmann, H. 2007. Geometric modeling in shape space. In ACM Transactions on Graphics (TOG), vol. 26, ACM, 64. Google ScholarDigital Library
15. Kircher, S., and Garland, M. 2008. Free-form motion processing. ACM Transactions on Graphics (TOG) 27, 2, 12. Google ScholarDigital Library
16. Klassen, E., Srivastava, A., Mio, M., and Joshi, S. 2004. Analysis of planar shapes using geodesic paths on shape spaces. Pattern Analysis and Machine Intelligence, IEEE Transactions on 26, 3, 372–383. Google ScholarDigital Library
17. Lipman, Y., Sorkine, O., Levin, D., and Cohen-Or, D. 2005. Linear rotation-invariant coordinates for meshes. ACM Transactions on Graphics (TOG) 24, 3, 479–487. Google ScholarDigital Library
18. Lipman, Y., Kim, V., and Funkhouser, T. 2012. Simple formulas for quasiconformal plane deformations. ACM Transactions on Graphics (TOG) 31, 5, 124. Google ScholarDigital Library
19. Lipman, Y. 2012. Bounded distortion mapping spaces for triangular meshes. ACM Transactions on Graphics (TOG) 31, 4, 108. Google ScholarDigital Library
20. Liu, L., Wang, G., Zhang, B., Guo, B., and Shum, H. 2004. Perceptually based approach for planar shape morphing. In Computer Graphics and Applications, 2004. PG 2004. Proceedings. 12th Pacific Conference on, IEEE, 111–120. Google ScholarDigital Library
21. Liu, L., Zhang, L., Xu, Y., Gotsman, C., and Gortler, S. J. 2008. A local/global approach to mesh parameterization. In Computer Graphics Forum, vol. 27, Wiley Online Library, 1495–1504. Google ScholarDigital Library
22. Sederberg, T., and Greenwood, E. 1992. A physically based approach to 2–d shape blending. In ACM SIGGRAPH Computer Graphics, vol. 26, ACM, 25–34. Google ScholarDigital Library
23. Shapira, M., and Rappoport, A. 1995. Shape blending using the star-skeleton representation. Computer Graphics and Applications, IEEE 15, 2, 44–50. Google ScholarDigital Library
24. Sheffer, A., and Kraevoy, V. 2004. Pyramid coordinates for morphing and deformation. In 3D Data Processing, Visualization and Transmission, 2004. 3DPVT 2004. Proceedings. 2nd International Symposium on, IEEE, 68–75. Google ScholarDigital Library
25. Sorkine, O., and Alexa, M. 2007. As-rigid-as-possible surface modeling. In ACM International Conference Proceeding Series, vol. 257, Citeseer, 109–116. Google ScholarDigital Library
26. Springborn, B., Schröder, P., and Pinkall, U. 2008. Conformal equivalence of triangle meshes. ACM Trans. Graph. 27, 3 (Aug.), 77:1–77:11. Google ScholarDigital Library
27. Surazhsky, T., and Elber, G. 2002. Metamorphosis of planar parametric curves via curvature interpolation. International Journal of Shape Modeling 8, 02, 201–216.Google ScholarCross Ref
28. Surazhsky, V., and Gotsman, C. 2001. Controllable morphing of compatible planar triangulations. ACM Transactions on Graphics 20, 4, 203–231. Google ScholarDigital Library
29. Surazhsky, V., and Gotsman, C. 2003. Intrinsic morphing of compatible triangulations. International Journal of Shape Modeling 9, 02, 191–201.Google ScholarCross Ref
30. Sykora, D., Dingliana, J., and Collins, S. 2009. As-rigid-as-possible image registration for hand-drawn cartoon animations. In Proceedings of the 7th International Symposium on Non-Photorealistic Animation and Rendering, ACM, 25–33. Google ScholarDigital Library
31. Weber, O., and Gotsman, C. 2010. Controllable conformal maps for shape deformation and interpolation. ACM Transactions on Graphics (TOG) 29, 4, 78. Google ScholarDigital Library
32. Weber, O., Myles, A., and Zorin, D. 2012. Computing extremal quasiconformal maps. In Computer Graphics Forum, vol. 31, Wiley Online Library, 1679–1689. Google ScholarDigital Library
33. Weintraub, S. 1997. Differential forms: a complement to vector calculus. Academic Press, San Diego.Google Scholar
34. Whited, B., and Rossignac, J. 2011. Ball-morph: Definition, implementation, and comparative evaluation. Visualization and Computer Graphics, IEEE Transactions on 17, 6, 757–769. Google ScholarDigital Library
35. Winkler, T., Drieseberg, J., Alexa, M., and Hormann, K. 2010. Multi-scale geometry interpolation. In Computer Graphics Forum, vol. 29, Wiley Online Library, 309–318.Google Scholar
36. Wolberg, G. 1998. Image morphing: a survey. The visual computer 14, 8, 360–372.Google Scholar
37. Xu, D., Zhang, H., Wang, Q., and Bao, H. 2006. Poisson shape interpolation. Graphical models 68, 3, 268–281. Google ScholarDigital Library
38. Zeng, W., Luo, F., Yau, S., and Gu, X. 2009. Surface quasi-conformal mapping by solving beltrami equations. Mathematics of Surfaces XIII, 391–408. Google ScholarDigital Library