“Patching Catmull-Clark meshes” by Peters
Conference:
Type(s):
Title:
- Patching Catmull-Clark meshes
Presenter(s)/Author(s):
Abstract:
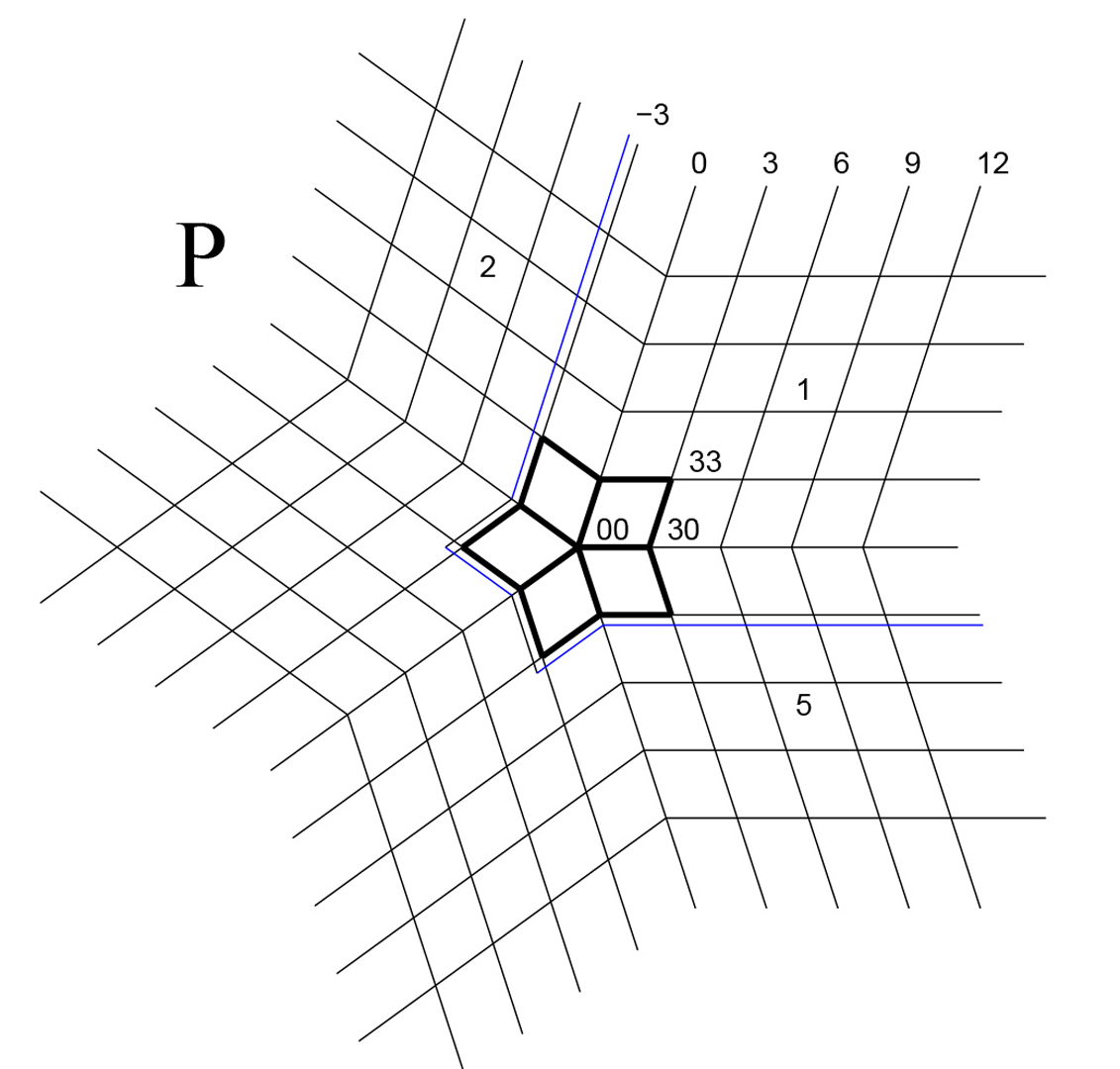
Named after the title, the PCCM transformation is a simple, explicit algorithm that creates large, smoothly joining bicubic Nurbs patches from a refined Catmull-Clark subdivision mesh. The resulting patches are maximally large in the sense that one patch corresponds to one quadrilateral facet of the initial, coarsest quadrilateral mesh before subdivision. The patches join parametrically C2 and agree with the Catmull-Clark limit surface except in the immediate neighborhood of extraordinary mesh nodes; in such a neighborhood they join at least with tangent continuity and interpolate the limit of the extraordinary mesh node. The PCCM transformation integrates naturally with array-based implementations of subdivision surfaces.
References:
1. A. A. Ball and D. J. T. Storry. Conditions for tangent plane continuity over recursively generated B-spline surfaces. ACM Trans. on Graphics,7:83-102, July 1988.
2. E. Catmull and J. Clark. Recursively generated B-spline sur-faces on arbitrary topological meshes. Computer Aided De-sign, 10:350-355, Oct 1978.
3. Tony DeRose, Michael Kass, and Tien Truong. Subdivision surfaces in character animation. Proceedings of SIGGRAPH 98, pages 85-94, July 1998.
4. OpenGL Foundation. http://trant.sgi.com/opengl/docs/man pages/hardcopy/GL/html/glu/nurbssurface.html.
5. Cindy M. Grimm and John F. Hughes. Modeling surfaces of arbitrary topology using manifolds. Proceedings of SIG-GRAPH 95, pages 359-368, August 1995.
6. Mark Halstead, Michael Kass, and Tony DeRose. Efficient, fair interpolation using Catmull-Clark surfaces. Proceedings of SIGGRAPH 93, pages 35-44, August 1993.
7. Adi Levin. Interpolating nets of curves by smooth subdivision surfaces. Computer Graphics, 33:57-64, 1999. Appendix.
8. A. H. Nasri. Boundary-corner control in recusive subdivision surfaces. CAD, 23(6):405-410, 1991.
9. A. H. Nasri and J. Peters. Computing volumes of solids en-closed by recursive subdivision surfaces. Comp. Gr. Forum, 16(3), September 1997.
10. J. Peters. C 1 -surface splines. SIAM J. Numer. Anal., 32(2):645-666, 1995.
11. J. Peters and U. Reif. Analysis of generalized B-spline subdi-vision algorithms. SIAM J. on Numer. Anal., 35(2):728-748, April 1998.
12. H. Prautzsch. Freeform splines. CAGD, 14(3):201-206, 1997.
13. Jos Stam. Exact evaluation of Catmull-Clark subdivision surfaces at arbitrary parameter values. Proceedings of SIG-GRAPH 98, pages 395-404, July 1998.
14. D. Zorin. Subdivision and multiresolution surface represen-tation. PhD thesis, Caltech, 1997.
15. D. Zorin. Implementing subdivision and multiresolution meshes. Chapter 6 of Course notes 37 of SIGGRAPH 99, Aug 1999.