“Parameterizing subdivision surfaces” by He, Schaefer and Hormann

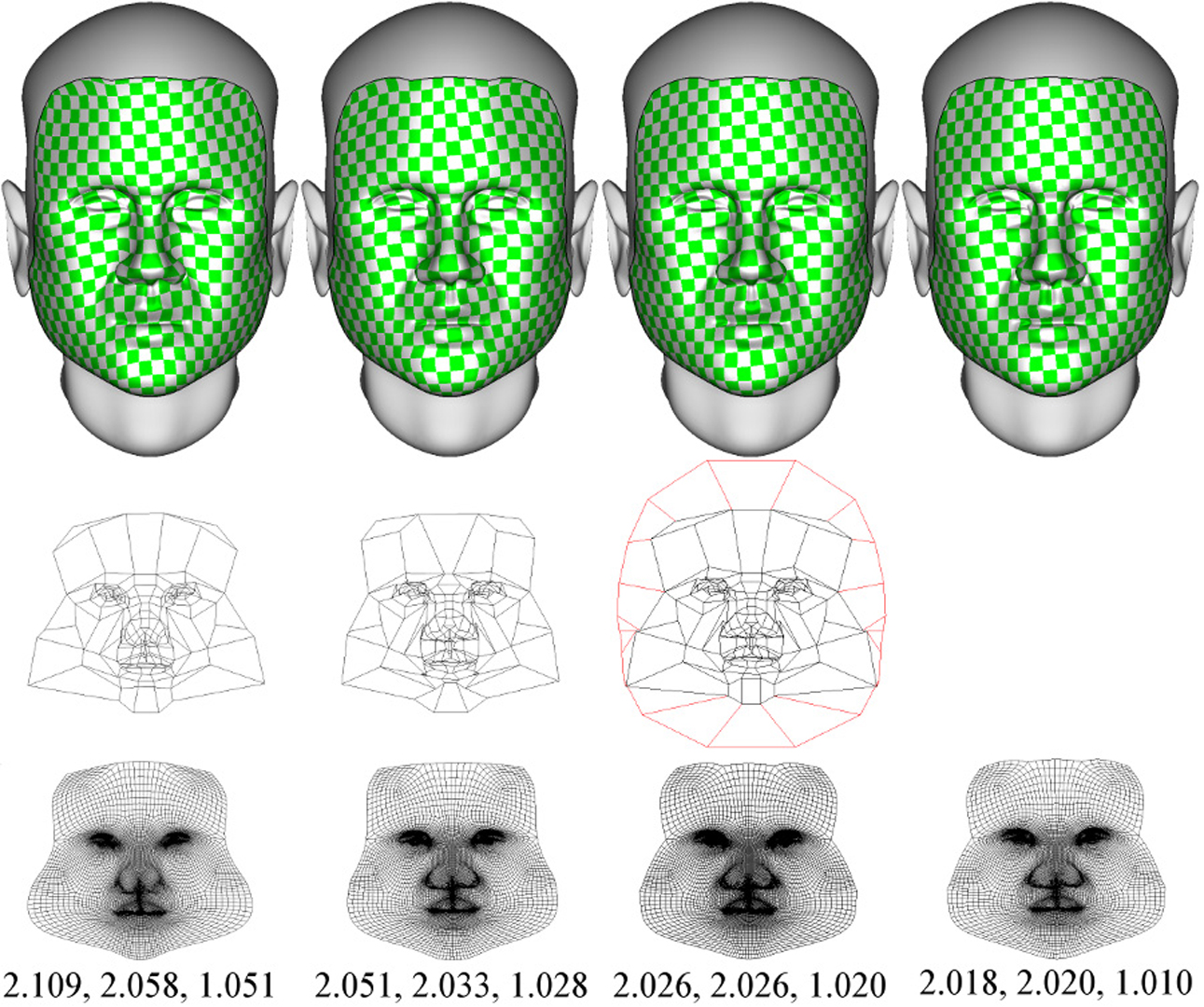
We present a method for parameterizing subdivision surfaces in an as-rigid-as-possible fashion. While much work has concentrated on parameterizing polygon meshes, little if any work has focused on subdivision surfaces despite their popularity. We show that polygon parameterization methods produce suboptimal results when applied to subdivision surfaces and describe how these methods may be modified to operate on subdivision surfaces. We also describe a method for creating extended charts to further reduce the distortion of the parameterization. Finally we demonstrate how to take advantage of the multi-resolution structure of subdivision surfaces to accelerate convergence of our optimization.

1. Aksoylu, B., Khodakovsky, A., and Schröder, P. 2005. Multilevel solvers for unstructured surface meshes. SIAM Journal on Scientific Computing 26, 4, 1146–1165. Google ScholarDigital Library
2. Ben-Chen, M., Gotsman, C., and Bunin, G. 2008. Conformal flattening by curvature prescription and metric scaling. Computer Graphics Forum 27, 2, 449–458.Google ScholarCross Ref
3. Biermann, H., Levin, A., and Zorin, D. 2000. Piecewise smooth subdivision surfaces with normal control. In Proceedings of SIGGRAPH, 113–120. Google ScholarDigital Library
4. Catmull, E., and Clark, J. 1978. Recursively generated Bspline surfaces on arbitrary topological meshes. Computer-Aided Design 10, 6, 350–355.Google ScholarCross Ref
5. Degener, P., Meseth, J., and Klein, R. 2003. An adaptable surface parameterization method. In Proceedings of the 12th International Meshing Roundtable, 201–213.Google Scholar
6. DeRose, T., Kass, M., and Truong, T. 1998. Subdivision surfaces in character animation. In Proceedings of SIGGRAPH, 85–94. Google ScholarDigital Library
7. Desbrun, M., Meyer, M., and Alliez, P. 2002. Intrinsic parameterizations of surface meshes. Computer Graphics Forum 21, 3, 209–218.Google ScholarCross Ref
8. Dominitz, A., and Tannenbaum, A. 2010. Texture mapping via optimal mass transport. IEEE Trans. on Visualization and Computer Graphics 16, 3, 419–433. Google ScholarDigital Library
9. Drone, S., Lee, M., and Oneppo, M., 2008. Direct3D 11 Tessellation. http://www.microsoft.com/downloads/details.aspx?FamilyId=2D5BC492-0E5C-4317-8170-E952DCA10D46.Google Scholar
10. Floater, M. S., and Hormann, K. 2005. Surface parameterization: a tutorial and survey. In Advances in Multiresolution for Geometric Modelling, N. A. Dodgson, M. S. Floater, and M. A. Sabin, Eds. Springer, 157–186.Google Scholar
11. Hormann, K., and Greiner, G. 2000. MIPS: An efficient global parametrization method. In Curve and Surface Design: Saint-Malo 1999, P.-J. Laurent, P. Sablonnière, and L. L. Schumaker, Eds. Vanderbilt University Press, 153–162.Google Scholar
12. Hormann, K., Greiner, G., and Campagna, S. 1999. Hierarchical parametrization of triangulated surfaces. In Proceedings of Vision, Modeling, and Visualization, 219–226.Google Scholar
13. Hormann, K., Lévy, B., and Sheffer, A. 2007. Mesh parameterization: Theory and practice. In SIGGRAPH 2007 Course Notes, no. 2. Google ScholarDigital Library
14. Kälberer, F., Nieser, M., and Polthier, K. 2007. Quadcover—surface parameterization using branched coverings. Computer Graphics Forum 26, 3, 375–384.Google ScholarCross Ref
15. Kharevich, L., Springborn, B., and Schröder, P. 2006. Discrete conformal mappings via circle patterns. ACM Transactions on Graphics 25, 2, 412–438. Google ScholarDigital Library
16. Kreyszig, E. 1991. Differential Geometry. Dover, New York.Google Scholar
17. Lambert, J. H. 1772. Beyträge zum Gebrauche der Mathematik und deren Anwendung, vol. 3. Buchhandlung der Realschule, Berlin.Google Scholar
18. Lévy, B., Petitjean, S., Ray, N., and Maillot, J. 2002. Least squares conformal maps for automatic texture atlas generation. ACM Transactions on Graphics 21, 3, 362–371. Google ScholarDigital Library
19. Liu, L., Zhang, L., Xu, Y., Gotsman, C., and Gortler, S. J. 2008. A local/global approach to mesh parameterization. Computer Graphics Forum 27, 5, 1495–1504.Google ScholarDigital Library
20. Loop, C., and Schaefer, S. 2008. Approximating Catmull–Clark subdivision surfaces with bicubic patches. ACM Transactions on Graphics 27, 1, 8:1–8:11. Google ScholarDigital Library
21. Maillot, J., Yahia, H., and Verroust, A. 1993. Interactive texture mapping. In Proceedings of SIGGRAPH, 27–34. Google ScholarDigital Library
22. Mercator, G. 1569. Nova et aucta orbis terrae descriptio ad usum navigantium emendate accommodata. Duisburg.Google Scholar
23. Pietroni, N., Tarini, M., and Cignoni, P. 2010. Almost isometric mesh parameterization through abstract domains. IEEE Trans. on Visualization and Computer Graphics. To appear. Google ScholarDigital Library
24. Piponi, D., and Borshukov, G. 2000. Seamless texture mapping of subdivision surfaces by model pelting and texture blending. In Proceedings of SIGGRAPH, 471–478. Google ScholarDigital Library
25. Ray, N., and Lévy, B. 2003. Hierarchical least squares conformal maps. In Proceedings of Pacific Graphics, 263–270. Google ScholarDigital Library
26. Sander, P. V., Snyder, J., Gortler, S. J., and Hoppe, H. 2001. Texture mapping progressive meshes. In Proceedings of SIGGRAPH, 409–416. Google ScholarDigital Library
27. Sheffer, A., Lévy, B., Mogilnitsky, M., and Bogomyakov, A. 2005. ABF++: fast and robust angle based flattening. ACM Transactions on Graphics 24, 2, 311–330. Google ScholarDigital Library
28. Sheffer, A., Praun, E., and Rose, K. 2006. Mesh parameterization methods and their applications. Foundations and Trends in Computer Graphics and Vision 2, 2, 105–171. Google ScholarDigital Library
29. Sorkine, O., Cohen-Or, D., Goldenthal, R., and Lischinski, D. 2002. Bounded-distortion piecewise mesh parametrization. In Proceedings of IEEE Visualization, 355–362. Google ScholarDigital Library
30. Springborn, B., Schröder, P., and Pinkall, U. 2008. Conformal equivalence of triangle meshes. ACM Transactions on Graphics 27, 3, 77:1–77:11. Google ScholarDigital Library
31. Tarini, M., Hormann, K., Cignoni, P., and Montani, C. 2004. PolyCube-Maps. ACM Transactions on Graphics 23, 3, 853–860. Google ScholarDigital Library
32. Woo, A. 1998. Chordlength texturing of spline surfaces. Journal of Graphics Tools 3, 2, 15–19. Google ScholarDigital Library