“P2M: A Fast Solver for Querying Distance from Point to Mesh Surface” by Chen, Xu, Song, Chen, Xin, et al. …
Conference:
Type(s):
Title:
- P2M: A Fast Solver for Querying Distance from Point to Mesh Surface
Session/Category Title: Making Contact: Simulating and Detecting Collisions
Presenter(s)/Author(s):
Moderator(s):
Abstract:
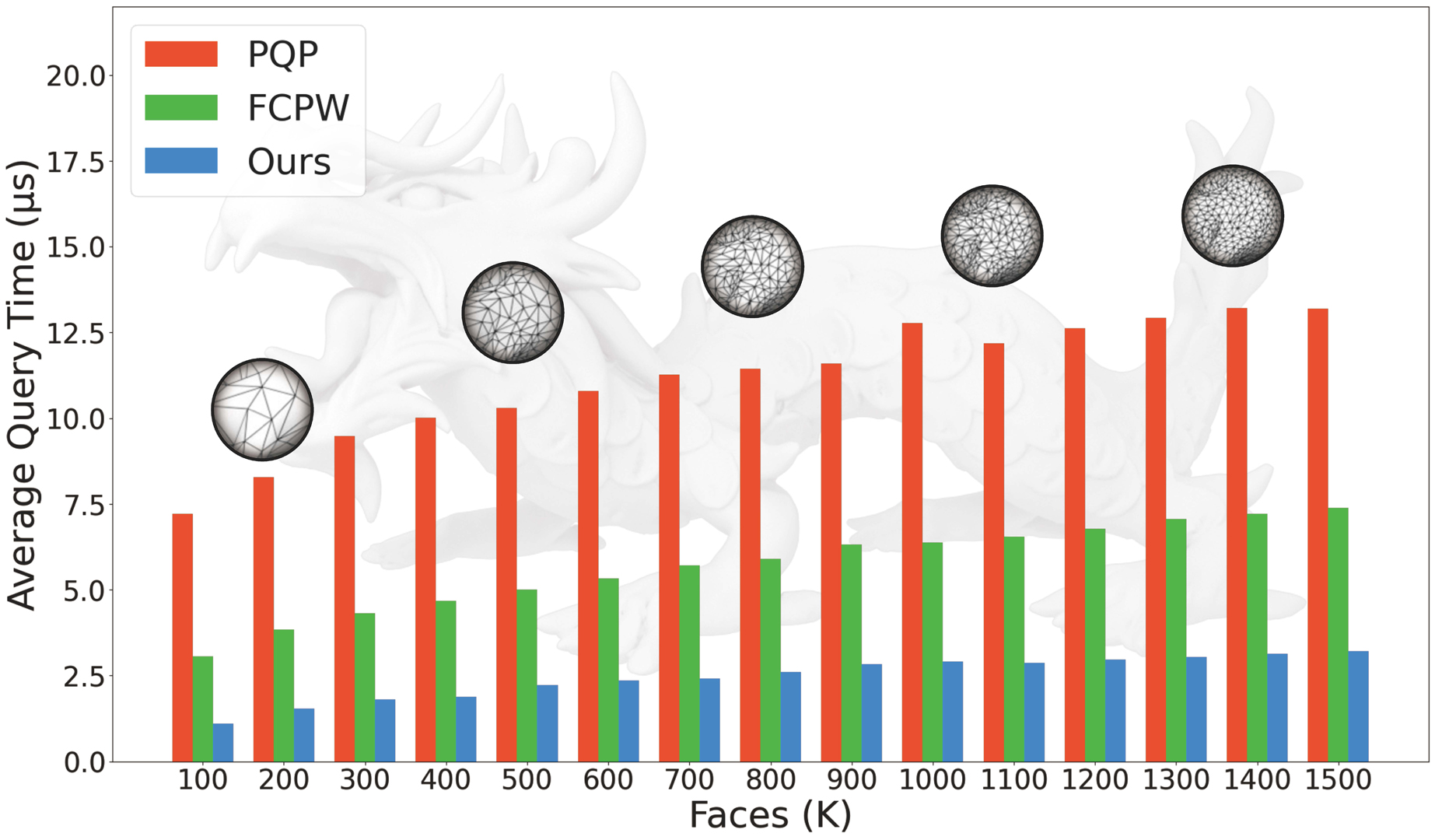
Most of the existing point-to-mesh distance query solvers, such as Proximity Query Package (PQP), Embree and Fast Closest Point Query (FCPW), are based on bounding volume hierarchy (BVH). The hierarchical organizational structure enables one to eliminate the vast majority of triangles that do not help find the closest point. In this paper, we develop a totally different algorithmic paradigm, named P2M, to speed up point-to-mesh distance queries. Our original intention is to precompute a KD tree (KDT) of mesh vertices to approximately encode the geometry of a mesh surface containing vertices, edges and faces. However, it is very likely that the closest primitive to the query point is an edge e (resp., a face f), but the KDT reports a mesh vertex υ instead. We call υ an interceptor of e (resp., f). The main contribution of this paper is to invent a simple yet effective interception inspection rule and an efficient flooding interception inspection algorithm for quickly finding out all the interception pairs. Once the KDT and the interception table are precomputed, the query stage proceeds by first searching the KDT and then looking up the interception table to retrieve the closest geometric primitive. Statistics show that our query algorithm runs many times faster than the state-of-the-art solvers.
References:
1. Mohammad Reza Abbasifard, Bijan Ghahremani, and Hassan Naderi. 2014. A survey on nearest neighbor search methods. International Journal of Computer Applications 95, 25 (2014).
2. Attila T Áfra, Ingo Wald, Carsten Benthin, and Sven Woop. 2016. Embree ray tracing kernels: overview and new features. ACM SIGGRAPH 2016 Talks (2016), 1–2.
3. Stefan Auer and Rüdiger Westermann. 2013. A semi-Lagrangian closest point method for deforming surfaces. In Computer Graphics Forum, Vol. 32. Wiley Online Library, 207–214.
4. Gill Barequet, Bernard Chazelle, Leonidas J Guibas, Joseph SB Mitchell, and Ayellet Tal. 1996. BOXTREE: A hierarchical representation for surfaces in 3D. In Computer Graphics Forum, Vol. 15. Wiley Online Library, 387–396.
5. Norbert Beckmann, Hans-Peter Kriegel, Ralf Schneider, and Bernhard Seeger. 1990. The R*-tree: An efficient and robust access method for points and rectangles. In Proceedings of the 1990 ACM SIGMOD international conference on Management of data. 322–331.
6. Stefan Berchtold, Daniel A Keim, and Hans-Peter Kriegel. 1996. The X-tree: An index structure for high-dimensional data. In Very Large Data-Bases. 28–39.
7. CGAL. 2022. The Computational Geometry Algorithms Library. https://www.cgal.org/.
8. Daniel S Coming and Oliver G Staadt. 2007. Velocity-aligned discrete oriented polytopes for dynamic collision detection. IEEE Transactions on Visualization and Computer Graphics 14, 1 (2007), 1–12.
9. Luc Devroye, Christophe Lemaire, and Jean-Michel Moreau. 2004. Expected time analysis for Delaunay point location. Computational Geometry 29, 2 (2004), 61–89.
10. Stephen A Ehmann and Ming C Lin. 2001. Accurate and fast proximity queries between polyhedra using convex surface decomposition. In Computer Graphics Forum, Vol. 20. Wiley Online Library, 500–511.
11. Christoph Funfzig, Torsten Ullrich, and Dieter W Fellner. 2006. Hierarchical spherical distance fields for collision detection. IEEE Computer Graphics and Applications 26, 1 (2006), 64–74.
12. Geogram. 2020. A programming library of geometric algorithms. http://alice.loria.fr/software/geogram/doc/html/index.html.
13. Stefan Gottschalk, Ming C Lin, and Dinesh Manocha. 1996. OBBTree: A hierarchical structure for rapid interference detection. In Proceedings of the 23rd annual conference on Computer graphics and interactive techniques. 171–180.
14. Andre Guezlec. 2001. ” Meshsweeper”: dynamic point-to-polygonal mesh distance and applications. IEEE Transactions on Visualization and Computer Graphics 7, 1 (2001), 47–61.
15. Leonidas J Guibas, An Thanh Nguyen, and Li Zhang. 2003. Zonotopes as bounding volumes. In SODA, Vol. 3. 803–812.
16. Antonin Guttman. 1984. R-trees: A dynamic index structure for spatial searching. In Proceedings of the 1984 ACM SIGMOD international conference on Management of data. 47–57.
17. Herman J Haverkort. 2004. Introduction to bounding volume hierarchies. Part of the PhD thesis, Utrecht University (2004).
18. Hugues Hoppe, Tony DeRose, Tom Duchamp, John McDonald, and Werner Stuetzle. 1993. Mesh optimization. In Proceedings of the 20th annual conference on Computer graphics and interactive techniques. 19–26.
19. Philip Martyn Hubbard. 1995. Collision detection for interactive graphics applications. IEEE Transactions on Visualization and Computer Graphics 1, 3 (1995), 218–230.
20. Ibrahim Kamel and Christos Faloutsos. 1993. Hilbert R-tree: An improved R-tree using fractals. Technical Report.
21. Norio Katayama and Shin’ichi Satoh. 1997. The SR-tree: An index structure for high-dimensional nearest neighbor queries. ACM Sigmod Record 26, 2 (1997), 369–380.
22. Ladislav Kavan and Jiří Žára. 2005. Fast collision detection for skeletally deformable models. In Computer Graphics Forum, Vol. 24. Blackwell Publishing, Inc Oxford, UK and Boston, USA, 363–372.
23. James T Klosowski, Martin Held, Joseph SB Mitchell, Henry Sowizral, and Karel Zikan. 1998. Efficient collision detection using bounding volume hierarchies of k-DOPs. IEEE Transactions on Visualization and Computer Graphics 4, 1 (1998), 21–36.
24. E. Scott Larsen, Stefan Gottschalk, Ming C. Lin, and Dinesh Manocha. 1999. Fast Proximity Queries with Swept Sphere Volumes.
25. Thomas Larsson and Tomas Akenine-Möller. 2006. A dynamic bounding volume hierarchy for generalized collision detection. Computers & Graphics 30, 3 (2006), 450–459.
26. Wen Li, Ying Zhang, Yifang Sun, Wei Wang, Mingjie Li, Wenjie Zhang, and Xuemin Lin. 2019. Approximate nearest neighbor search on high dimensional data—experiments, analyses, and improvement. IEEE Transactions on Knowledge and Data Engineering 32, 8 (2019), 1475–1488.
27. Shengjun Liu and Charlie CL Wang. 2010. Fast intersection-free offset surface generation from freeform models with triangular meshes. IEEE Transactions on Automation Science and Engineering 8, 2 (2010), 347–360.
28. Shengjun Liu, Charlie CL Wang, Kin-Chuen Hui, Xiaogang Jin, and Hanli Zhao. 2007. Ellipsoid-tree construction for solid objects. In Proceedings of the 2007 ACM symposium on Solid and physical modeling. 303–308.
29. Ting Liu, Andrew W Moore, Alexander Gray, and Claire Cardie. 2006. New Algorithms for Efficient High-Dimensional Nonparametric Classification. Journal of Machine Learning Research 7, 6 (2006).
30. Daniel Meister, Shinji Ogaki, Carsten Benthin, Michael J Doyle, Michael Guthe, and Jiří Bittner. 2021. A Survey on Bounding Volume Hierarchies for Ray Tracing. In Computer Graphics Forum, Vol. 40. Wiley Online Library, 683–712.
31. Ian J. Palmer and Richard L. Grimsdale. 1995. Collision detection for animation using sphere-trees. In Computer Graphics Forum, Vol. 14. Wiley Online Library, 105–116.
32. Tan Ruipu, Zhao Wei, and Li Jing. 2010. The Study of Parallel Collision Detection Algorithms. In 2010 International Conference on Multimedia Technology. IEEE, 1–4.
33. Yasushi Sakurai, Masatoshi Yoshikawa, Shunsuke Uemura, Haruhiko Kojima, et al. 2000. The A-tree: An index structure for high-dimensional spaces using relative approximation. In VLDB, Vol. 2000. Citeseer, 5–16.
34. Rohan Sawhney. 2021. FCPW: Fastest Closest Points in the West. https://github.com/rohan-sawhney/fcpw.
35. Mehdi Sharifzadeh and Cyrus Shahabi. 2010. VoR-Tree: R-Trees with Voronoi Diagrams for Efficient Processing of Spatial Nearest Neighbor Queries. Proc. VLDB Endow. 3, 1–2 (sep 2010), 1231–1242.
36. Hang Si. 2015. TetGen, a Delaunay-Based Quality Tetrahedral Mesh Generator. ACM Transactions on Mathematical Software (TOMS) 41 (2015), 1–36.
37. Min Tang, Dinesh Manocha, Jiang Lin, and Ruofeng Tong. 2011. Collision-streams: Fast GPU-based collision detection for deformable models. In Symposium on interactive 3D graphics and games. 63–70.
38. Ingo Wald, Will Usher, Nathan Morrical, Laura Lediaev, and Valerio Pascucci. 2019. RTX Beyond Ray Tracing: Exploring the Use of Hardware Ray Tracing Cores for Tet-Mesh Point Location.. In High Performance Graphics (Short Papers). 7–13.
39. Charlie CL Wang and Yong Chen. 2013. Thickening freeform surfaces for solid fabrication. Rapid Prototyping Journal 19, 6 (2013), 395–406.
40. Monan Wang and Jiaqi Cao. 2021. A review of collision detection for deformable objects. Computer Animation and Virtual Worlds (2021), e1987.
41. David A White and Ramesh Jain. 1996. Similarity indexing with the SS-tree. In Proceedings of the Twelfth International Conference on Data Engineering. IEEE, 516–523.
42. Robin Ytterlid and Evan Shellshear. 2015. BVH split strategies for fast distance queries. Journal of Computer Graphics Techniques (JCGT) 4, 1 (2015), 1–25.
43. Qingnan Zhou and Alec Jacobson. 2016. Thingi10K: A Dataset of 10,000 3D-Printing Models.