“Out-of-core simplification of large polygonal models” by Lindstrom

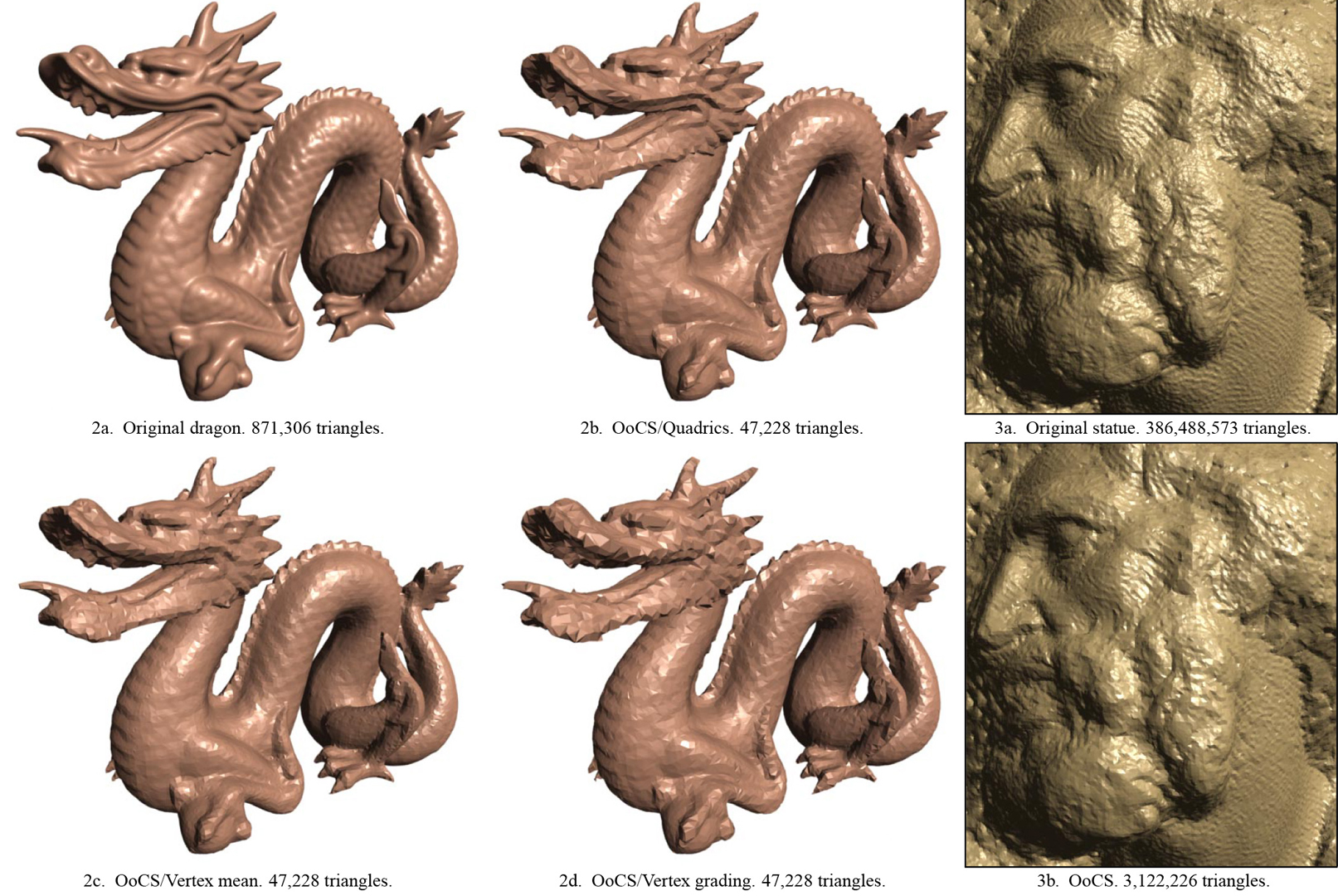
We present an algorithm for out-of-core simplification of large polygonal datasets that are too complex to fit in main memory. The algorithm extends the vertex clustering scheme of Rossignac and Borrel [13] by using error quadric information for the placement of each cluster’s representative vertex, which better preserves fine details and results in a low mean geometric error. The use of quadrics instead of the vertex grading approach in [13] has the additional benefits of requiring less disk space and only a single pass over the model rather than two. The resulting linear time algorithm allows simplification of datasets of arbitrary complexity.
In order to handle degenerate quadrics associated with (near) flat regions and regions with zero Gaussian curvature, we present a robust method for solving the corresponding underconstrained least-squares problem. The algorithm is able to detect these degeneracies and handle them gracefully. Key features of the simplification method include a bounded Hausdorff error, low mean geometric error, high simplification speed (up to 100,000 triangles/second reduction), output (but not input) sensitive memory requirements, no disk space overhead, and a running time that is independent of the order in which vertices and triangles occur in the mesh.

1. ACKERMAN, M. J. The Visible Human Project. In Proceedings of the IEEE, 86(3), March 1998, pp. 504-511. Project URL: http://ww~nlm.nih.gov/ research/visible.
2. BERNARDINI, F., MITTLEMAN, J., and RUSHMEIER, H. Case Study: Scanning Michelangelo’s Florentine Pieth. In ACM SIGGRAPH 99 Course Notes, Course 8, August 1999. Project URL: http://www.research.ibm, com/pieta.
3. BERNARDINI, F., MITTLEMAN, J., RUSHMEIER, H., SILVA, C., and TAUBIN, G. The Ball-Pivoting Algorithm for Surface Reconstruction. In IEEE Transactions on Visualization and Computer Graphics, 5(4), October-December 1999, pp. 349-359.
4. CHIANG, Y.-J., SILVA, C. T., and SCHROEDER, W. J. Interactive Out-of-Core Isosurface Extraction. In IEEE Visualization ’98 Proceedings, October 1998, pp. 167-174.
5. GARLAND, M. and HECKBERT, P. S. Surface Simplification using Quadric Error Metrics. Proceedings of SIGGRAPH 97. In Computer Graphics Proceedings, Annual Conference Series, 1997, ACM SIGGRAPH, pp. 209-216.
6. HOPPE, H. Smooth View-Dependent Level-of-Detail Control and its Application to Terrain Rendering. In IEEE Visualization ’98 Proceedings, October 1998, pp. 35-42.
7. LEVOY, M. The Digital Michelangelo Project. In proceedings of the Second international Conference on 3D Digital imaging and Modeling, October 1999, pp. 2-11. Project URL: http://graphics.stanford, edu/ projects~ mich.
8. LINDSTROM, P. and TURK, G. Fast and Memory Efficient Polygonal Simplification. In IEEE Visualization ’98 Proceedings, October 1998, pp. 279-286.
9. LOW, K.-L. and TAN, T.-S. Model Simplification using Vertex-Clustering. In Proceedings of}997 Symposium on interactive 3D Graphics, April 1997, pp. 75-82.
10. PHARR, M., KOLB, C., GERSHBEIN, R., and HANRAHAN, P. Rendering Complex Scenes with Memory-Coherent Ray Tracing. Proceedings of SIG- GRAPH 97. In Computer Graphics Proceedings, Annual Conference Series, 1997, ACM SIGGRAPH, pp. 101-108.
11. PRESS, W. H., TEUKOLSKY, S. A., VETTERLING, W. T., and FLANNERY, B. P. Numerical Recipes in C: The Art of Scientific Computing, Second Edition. Cambridge University Press, 1992, pp. 408-412.
12. RONFARD, R. and ROSSIGNAC, J. Full-Range Approximation of Triangulated Polyhedra. Proceedings of Eurographics 96. In Computer Graphics Forum, 15(3), August 1996, pp. 67-76.
13. ROSSIGNAC, J. and BORREL, P. Multi-Resolution 3D Approximations for Rendering Complex Scenes. In Modeling in Computer Graphics, edited by B. Falcidieno and T. L. Kunii, Springer-Verlag, 1993, pp. 455-465.