“On the convexity and feasibility of the bounded distortion harmonic mapping problem”
Conference:
Type(s):
Title:
- On the convexity and feasibility of the bounded distortion harmonic mapping problem
Session/Category Title: MAPPINGS
Presenter(s)/Author(s):
Moderator(s):
Abstract:
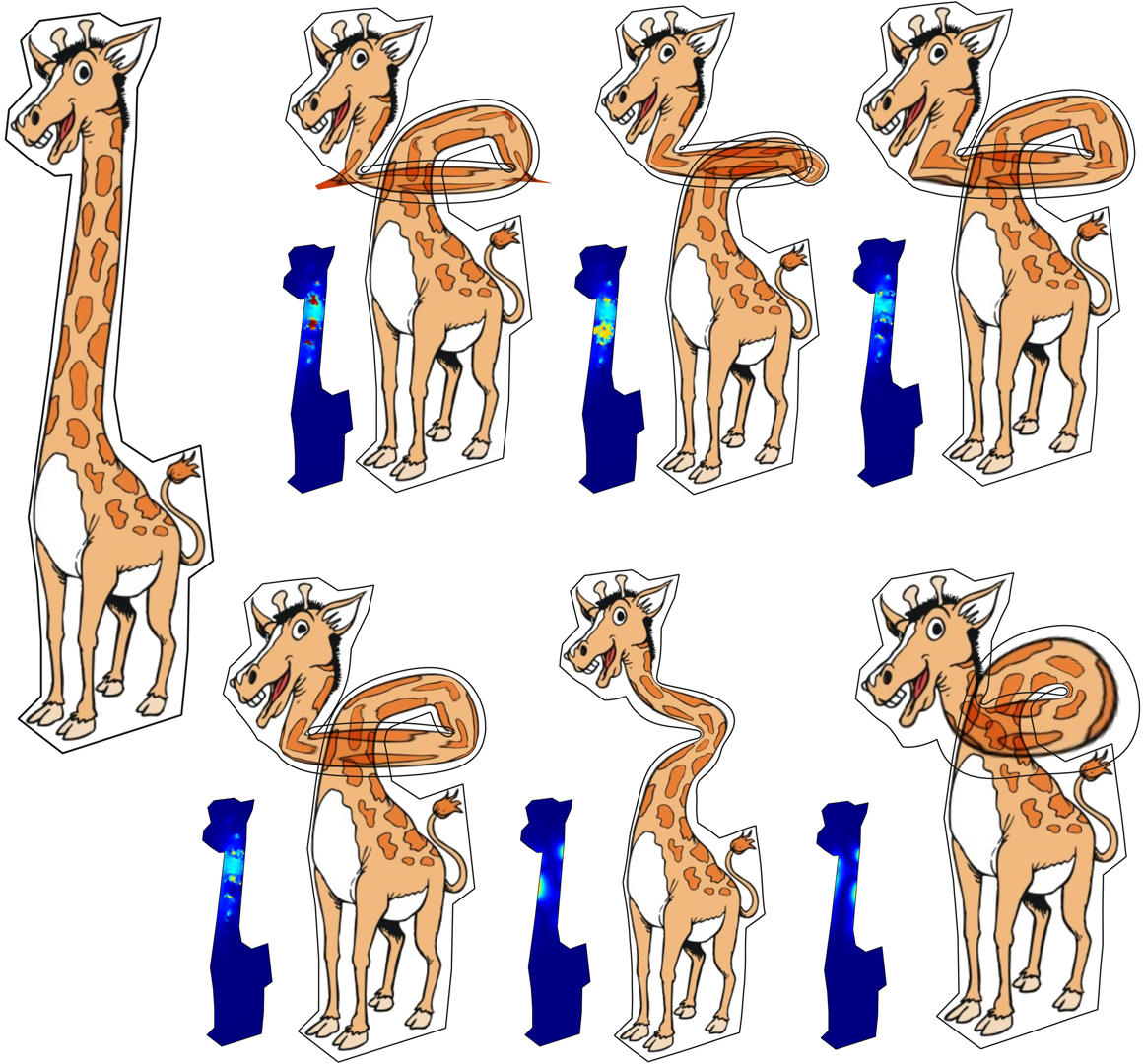
Computation of mappings is a central building block in many geometry processing and graphics applications. The pursuit to compute mappings that are injective and have a controllable amount of conformal and isometric distortion is a long endeavor which has received significant attention by the scientific community in recent years. The difficulty of the problem stems from the fact that the space of bounded distortion mappings is nonconvex. In this paper, we consider the special case of harmonic mappings which have been used extensively in many graphics applications. We show that, somewhat surprisingly, the space of locally injective planar harmonic mappings with bounded conformal and isometric distortion has a convex characterization. We describe several projection operators that, given an arbitrary input mapping, are guaranteed to output a bounded distortion locally injective harmonic mapping that is closest to the input mapping in some special sense. In contrast to alternative approaches, the optimization problems that correspond to our projection operators are shown to be always feasible for any choice of distortion bounds. We use the boundary element method (BEM) to discretize the space of planar harmonic mappings and demonstrate the effectiveness of our approach through the application of planar shape deformation.
References:
1. Ahlfors, L. 1979. Complex analysis, vol. 7. McGraw-Hill Education.Google Scholar
2. Aigerman, N., and Lipman, Y. 2013. Injective and bounded distortion mappings in 3D. TOG 32, 4, 106. Google ScholarDigital Library
3. Aigerman, N., Poranne, R., and Lipman, Y. 2014. Lifted bijections for low distortion surface mappings. TOG 33, 4, 69. Google ScholarDigital Library
4. Alexa, M. 2002. Recent advances in mesh morphing. In Computer Graphics Forum, vol. 21, 173–198.Google ScholarCross Ref
5. ApS, M. 2015. The MOSEK optimization toolbox for MATLAB manual. Version 7.1 (Revision 28).Google Scholar
6. Bell, S. R. 1992. The Cauchy transform, potential theory and conformal mapping, vol. 7. CRC press.Google Scholar
7. Bommes, D., Lévy, B., Pietroni, N., Puppo, E., Silva, C., Tarini, M., and Zorin, D. 2013. Quad-mesh generation and processing: A survey. Computer Graphics Forum 32, 6, 51–76. Google ScholarDigital Library
8. Botsch, M., and Sorkine, O. 2008. On linear variational surface deformation methods. TVCG 14, 1, 213–230. Google ScholarDigital Library
9. Boyd, S., and Vandenberghe, L. 2004. Convex optimization. Cambridge University Press. Google ScholarDigital Library
10. Chen, R., and Weber, O. 2015. Bounded distortion harmonic mappings in the plane. ACM TOG 34, 4, 73. Google ScholarDigital Library
11. Chien, E., Chen, R., and Weber, O. 2016. Bounded distortion harmonic shape interpolation. ACM TOG 35, 4. Google ScholarDigital Library
12. Duren, P. 2004. Harmonic mappings in the plane. Cambridge University Press.Google Scholar
13. Floater, M., and Hormann, K. 2005. Surface Parameterization: a Tutorial and Survey. Adv. Multi. Geom. Modelling.Google Scholar
14. Floater, M. 1997. Parametrization and smooth approximation of surface triangulations. CAGD 14, 3, 231–250. Google ScholarDigital Library
15. Grant, M., Boyd, S., and Ye, Y., 2008. Cvx: Matlab software for disciplined convex programming.Google Scholar
16. Hormann, K., and Greiner, G. 2000. Mips: An efficient global parametrization method. Curve and Surface Design: Saint-Malo 99, 153–162.Google Scholar
17. Joshi, P., Meyer, M., DeRose, T., and Green, B. 2007. Harmonic coordinates for character articulation. ACM TOG 26, 3, 71. Google ScholarDigital Library
18. Kharevych, L., Springborn, B., and Schröder, P. 2006. Discrete conformal mappings via circle patterns. ACM Trans. Graph. 25, 2, 412–438. Google ScholarDigital Library
19. Kovalsky, S. Z., Aigerman, N., Basri, R., and Lipman, Y. 2014. Controlling singular values with semidefinite programming. ACM TOG 33, 4. Google ScholarDigital Library
20. Kovalsky, S. Z., Aigerman, N., Basri, R., and Lipman, Y. 2015. Large-scale bounded distortion mappings. ACM TOG 34, 6, 191. Google ScholarDigital Library
21. Levi, Z., and Zorin, D. 2014. Strict minimizers for geometric optimization. ACM TOG 33, 6, 185. Google ScholarDigital Library
22. Lévy, B., Petitjean, S., Ray, N., and Maillot, J. 2002. Least squares conformal maps for automatic texture atlas generation. ACM TOG 21, 3, 362–371. Google ScholarDigital Library
23. Lipman, Y. 2012. Bounded distortion mapping spaces for triangular meshes. ACM TOG 31, 4, 108. Google ScholarDigital Library
24. Liu, L., Zhang, L., Xu, Y., Gotsman, C., and Gortler, S. 2008. A local/global approach to mesh parameterization. Computer Graphics Forum 27, 5, 1495–1504. Google ScholarDigital Library
25. Poranne, R., and Lipman, Y. 2014. Provably good planar mappings. ACM TOG 33, 4, 76. Google ScholarDigital Library
26. Schüller, C., Kavan, L., Panozzo, D., and Sorkine-Hornung, O. 2013. Locally injective mappings. In Computer Graphics Forum, vol. 32, 125–135. Google ScholarDigital Library
27. Sheffer, A., Praun, E., and Rose, K. 2006. Mesh Parameterization Methods and Their Applications. Found. Trends. Comput. Graph. Vis. 2, 2, 105–171. Google ScholarDigital Library
28. Sorkine, O., and Alexa, M. 2007. As-rigid-as-possible surface modeling. In SGP, 109–116. Google ScholarDigital Library
29. Sorkine, O. 2006. Differential representations for mesh processing. Computer Graphics Forum 25, 4, 789–807.Google ScholarCross Ref
30. Springborn, B., Schröder, P., and Pinkall, U. 2008. Conformal equivalence of triangle meshes. ACM TOG 27, 3, 77. Google ScholarDigital Library
31. Tutte, W. 1963. How to draw a graph. Proc. London Math. Soc 13, 3, 743–768.Google ScholarCross Ref
32. Weber, O., and Gotsman, C. 2010. Controllable conformal maps for shape deformation and interpolation. ACM TOG 29, 4. Google ScholarDigital Library
33. Weber, O., and Zorin, D. 2014. Locally injective parametrization with arbitrary fixed boundaries. TOG 33, 4, 75. Google ScholarDigital Library
34. Weber, O., Ben-Chen, M., and Gotsman, C. 2009. Complex barycentric coordinates with applications to planar shape deformation. Computer Graphics Forum 28, 2, 587–597.Google ScholarCross Ref
35. Weber, O., Myles, A., and Zorin, D. 2012. Computing extremal quasiconformal maps. Computer Graphics Forum 31, 5, 1679–1689. Google ScholarDigital Library
36. Weber, O. 2010. Hybrid Methods for Interactive Shape Manipulation. PhD thesis, Technion – Israel Institute of Technology.Google Scholar
37. Wolberg, G. 1998. Image morphing: a survey. The visual computer 14, 8, 360–372.Google Scholar