“New Types of Smooth Subdivision Algorithms” by Zaitseva
Conference:
Type(s):
Entry Number: 64
Title:
- New Types of Smooth Subdivision Algorithms
Presenter(s)/Author(s):
Abstract:
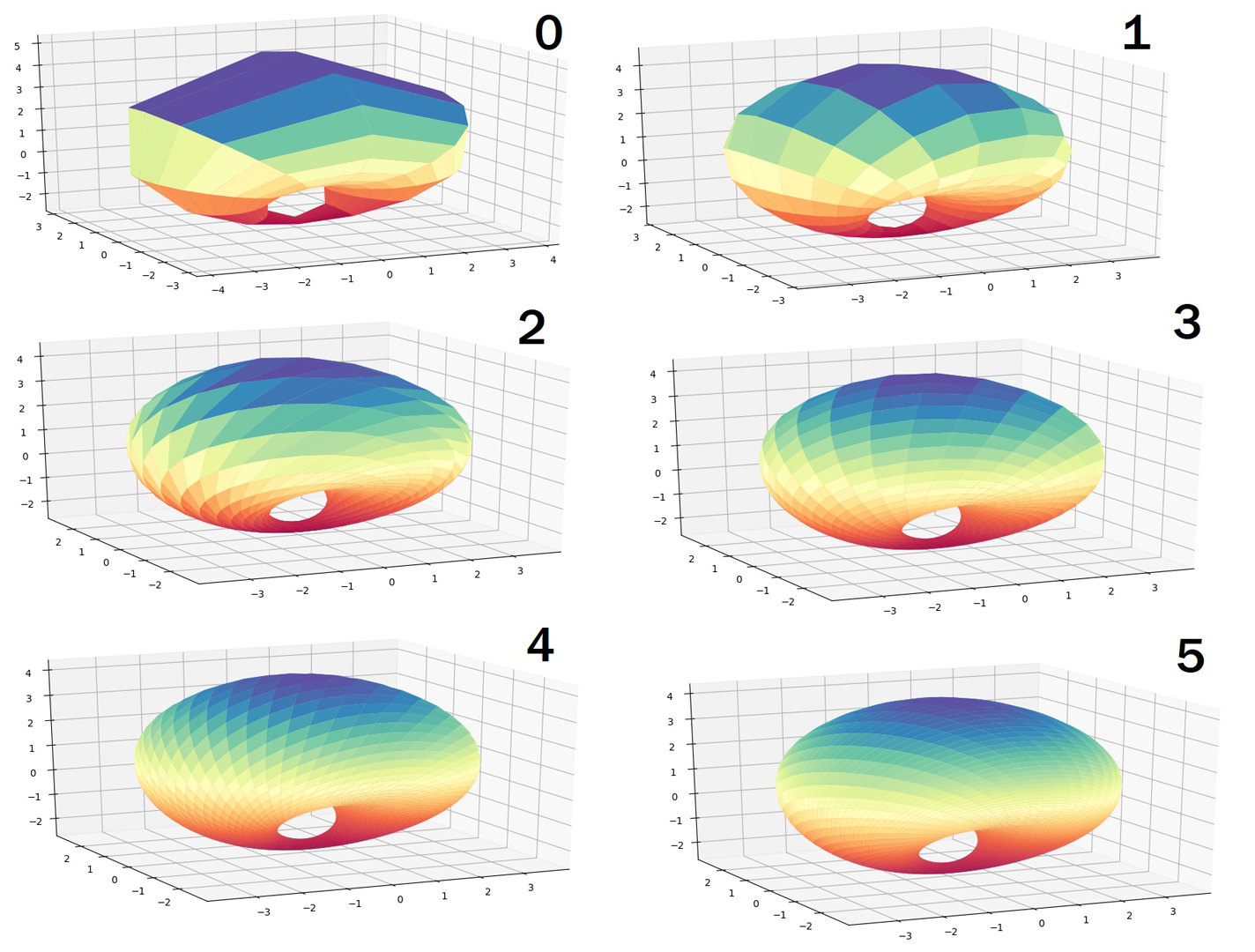
We suggest a new type of subdivision schemes based on matrix dilation for generating smooth surfaces. At each iteration, the number of the nodes in the mesh is doubled and the direction of their weighted averaging changes. The scheme has a low complexity because of a small number of coefficients (four, five or six). Using the recent techniques related to the notion of joint spectral characteristics of matrices, we find the smoothness of generated surfaces which in some cases is surprisingly better than for classical schemes.
References:
A.S. Cavaretta, W.D. Dahmen, and Ch.A. Micchelli. 1991. Stationary subdivision. American Mathematical Soc. 453, 3 (1991).Google Scholar
Maria Charina and Vladimir Protasov. 2019. Regularity of anisotropic refinable functions. J. Fourier Anal. Appl. 47, 3 (2019), 795–821. https://doi.org/10.1016/j.acha.2017.12.003Google Scholar
Chongyang Deng and Weiyin Ma. 2013. A unified interpolatory subdivision scheme for quadrilateral meshes. ACM Transactions on Graphics (TOG) 32, 3 (2013), 1–11. https://doi.org/10.1145/2487228.2487231Google ScholarDigital Library
J. C. Lagarias and Y. L. Wang. 1997. Integral self-affine tiles in Math 34. II. Lattice tilings. J. Fourier Anal. Appl. 3, 1 (1997), 83–102. https://doi.org/10.1007/s00041-001-4051-2Google ScholarCross Ref
Thomas Meystrik. 2020. Algorithm 1011: Improved Invariant Polytope Algorithm and Applications. ACM Transactions on Mathematical Software (TOMS) 46, 3 (2020), 1–26. https://doi.org/10.1145/3408891Google ScholarDigital Library
Luiz Velho and Denis Zorin. 2001. 4–8 Subdivision. Computer Aided Geometric Design 18, 5 (2001), 397–427. https://doi.org/10.1016/S0167-8396(01)00039-5Google ScholarDigital Library