“NeuralSound: learning-based modal sound synthesis with acoustic transfer” by Jin, Li, Wang and Manocha

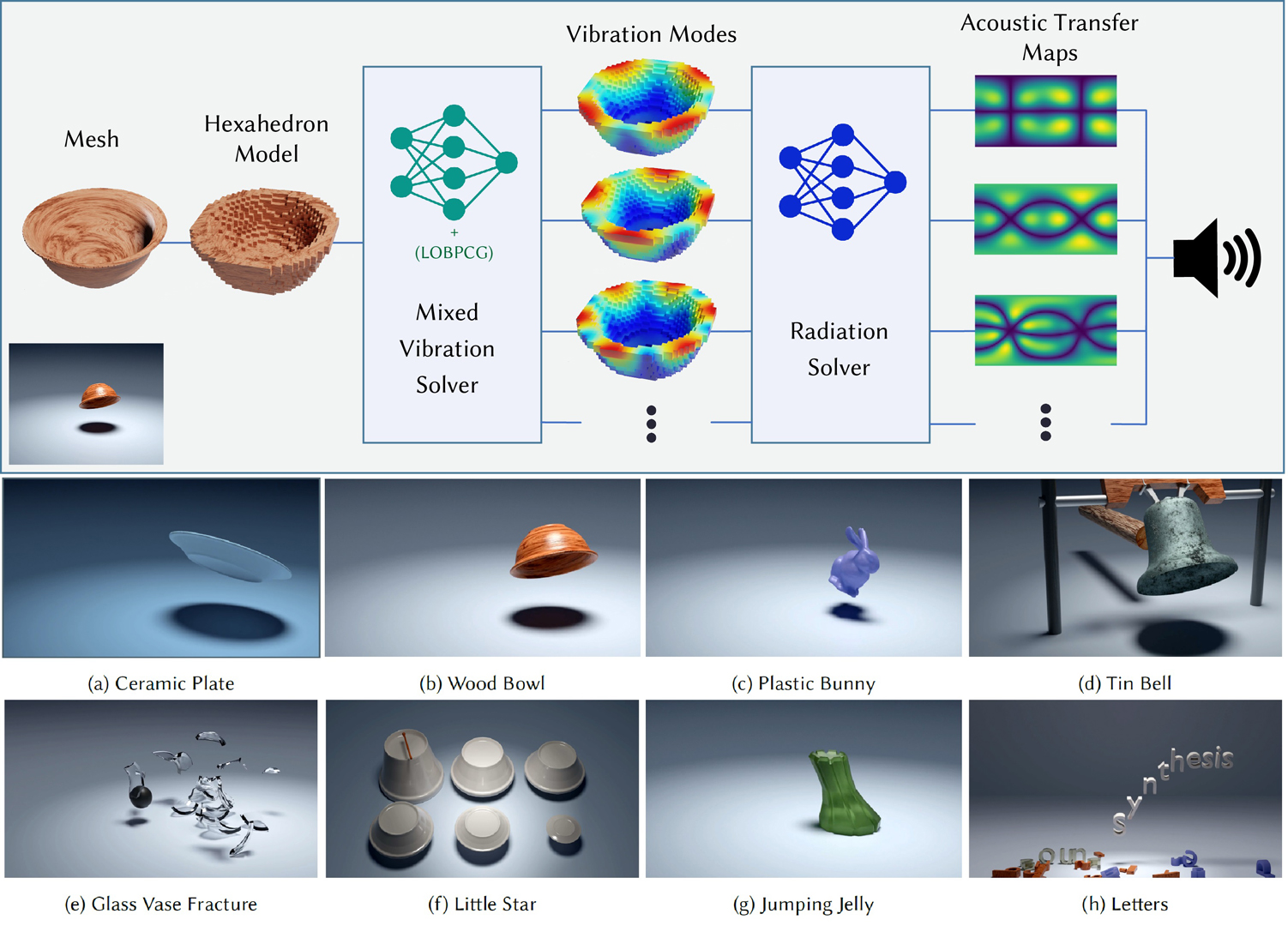
We present a novel learning-based modal sound synthesis approach that includes a mixed vibration solver for modal analysis and a radiation network for acoustic transfer. Our mixed vibration solver consists of a 3D sparse convolution network and a Locally Optimal Block Preconditioned Conjugate Gradient (LOBPCG) module for iterative optimization. Moreover, we highlight the correlation between a standard numerical vibration solver and our network architecture. Our radiation network predicts the Far-Field Acoustic Transfer maps (FFAT Maps) from the surface vibration of the object. The overall running time of our learning-based approach for most new objects is less than one second on a RTX 3080 Ti GPU while maintaining a high sound quality close to the ground truth solved by standard numerical methods. We also evaluate the numerical and perceptual accuracy of our approach on different objects with various shapes and materials.

1. Peter Arbenz, Ulrich L Hetmaniuk, Richard B Lehoucq, and Raymond S Tuminaro. 2005. A comparison of eigensolvers for large-scale 3D modal analysis using AMG-preconditioned iterative methods. Internat. J. Numer. Methods Engrg. 64, 2 (2005), 204–236.Google ScholarCross Ref
2. Timo Betcke and Matthew W Scroggs. 2021. Bempp-cl: A fast Python based just-in-time compiling boundary element library. Journal of Open Source Software 6, 59 (2021), 2879.Google ScholarCross Ref
3. Nicolas Bonneel, George Drettakis, Nicolas Tsingos, Isabelle Viaud-Delmon, and Doug James. 2008. Fast modal sounds with scalable frequency-domain synthesis. In ACM SIGGRAPH 2008 papers. 1–9.Google ScholarDigital Library
4. William L Briggs, Van Emden Henson, and Steve F McCormick. 2000. A multigrid tutorial. SIAM.Google Scholar
5. Jeffrey N Chadwick, Steven S An, and Doug L James. 2009. Harmonic shells: a practical nonlinear sound model for near-rigid thin shells. ACM Transactions on Graphics (Proceedings of SIGGRAPH 2009) 28, 5 (2009), 1–10.Google ScholarDigital Library
6. Jeffrey N. Chadwick, Changxi Zheng, and Doug L. James. 2012. Precomputed Acceleration Noise for Improved Rigid-Body Sound. ACM Transactions on Graphics (Proceedings of SIGGRAPH 2012) 31, 4 (Aug. 2012).Google Scholar
7. Christopher Choy, JunYoung Gwak, and Silvio Savarese. 2019. 4D Spatio-Temporal ConvNets: Minkowski Convolutional Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 3075–3084.Google ScholarCross Ref
8. Perry R. Cook. 1995. Integration of Physical Modeling for Synthesis and Animation. In Proceedings of the 1995 International Computer Music Conference, ICMC 1995, Banff, AB, Canada, September 3–7, 1995. Michigan Publishing.Google Scholar
9. Erwin Coumans and Yunfei Bai. 2016. Pybullet, a python module for physics simulation for games, robotics and machine learning. (2016).Google Scholar
10. Lothar Cremer and Manfred Heckl. 2013. Structure-borne sound: structural vibrations and sound radiation at audio frequencies. Springer Science & Business Media.Google Scholar
11. Jed A. Duersch, Meiyue Shao, Chao Yang, and Ming Gu. 2018. A Robust and Efficient Implementation of LOBPCG. SIAM Journal on Scientific Computing 40, 5 (2018), C655–C676.Google ScholarDigital Library
12. Benjamin Graham, Martin Engelcke, and Laurens Van Der Maaten. 2018. 3d semantic segmentation with submanifold sparse convolutional networks. In Proceedings of the IEEE conference on computer vision and pattern recognition. 9224–9232.Google ScholarCross Ref
13. Benjamin Graham and Laurens van der Maaten. 2017. Submanifold Sparse Convolutional Networks. arXiv preprint arXiv:1706.01307 (2017).Google Scholar
14. Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. 2016. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition. 770–778.Google ScholarCross Ref
15. Doug L. James. 2016. Physically Based Sound for Computer Animation and Virtual Environments. In ACM SIGGRAPH 2016 Courses (Anaheim, California) (SIGGRAPH ’16). Association for Computing Machinery, New York, NY, USA, Article 22, 8 pages.Google Scholar
16. Doug L James, Jernej Barbič, and Dinesh K Pai. 2006. Precomputed acoustic transfer: output-sensitive, accurate sound generation for geometrically complex vibration sources. ACM Transactions on Graphics (Proceedings of SIGGRAPH 2006) 25, 3 (2006), 987–995.Google ScholarDigital Library
17. Xutong Jin, Sheng Li, Tianshu Qu, Dinesh Manocha, and Guoping Wang. 2020. Deep-Modal: Real-Time Impact Sound Synthesis for Arbitrary Shapes. In Proceedings of the 28th ACM International Conference on Multimedia (Seattle, WA, USA) (MM ’20). Association for Computing Machinery, New York, NY, USA, 1171–1179.Google ScholarDigital Library
18. Diederik P Kingma and Jimmy Ba. 2015. Adam: A Method for Stochastic Optimization. In ICLR (Poster).Google Scholar
19. Stephen Kirkup. 2019. The boundary element method in acoustics: A survey. Applied Sciences 9, 8 (2019), 1642.Google ScholarCross Ref
20. Andrew Knyazev. 1997. New estimates for Ritz vectors. Mathematics of computation 66, 219 (1997), 985–995.Google Scholar
21. Andrew V Knyazev. 1998. Preconditioned eigensolvers—an oxymoron. Electron. Trans. Numer. Anal 7 (1998), 104–123.Google Scholar
22. Andrew V Knyazev. 2001. Toward the optimal preconditioned eigensolver: Locally optimal block preconditioned conjugate gradient method. SIAM journal on scientific computing 23, 2 (2001), 517–541.Google Scholar
23. Sebastian Koch, Albert Matveev, Zhongshi Jiang, Francis Williams, Alexey Artemov, Evgeny Burnaev, Marc Alexa, Denis Zorin, and Daniele Panozzo. 2019. ABC: A Big CAD Model Dataset For Geometric Deep Learning. In The IEEE Conference on Computer Vision and Pattern Recognition (CVPR).Google Scholar
24. Cornelius Lanczos. 1950. An iteration method for the solution of the eigenvalue problem of linear differential and integral operators. United States Governm. Press Office Los Angeles, CA.Google Scholar
25. Timothy R. Langlois, Steven S. An, Kelvin K. Jin, and Doug L. James. 2014. Eigenmode Compression for Modal Sound Models. ACM Transactions on Graphics (Proceedings of SIGGRAPH 2014) 33, 4 (Aug. 2014).Google Scholar
26. R. B. Lehoucq, D. C. Sorensen, and C. Yang. 1997. ARPACK Users Guide: Solution of Large Scale Eigenvalue Problems by Implicitly Restarted Arnoldi Methods.Google Scholar
27. Dingzeyu Li, Yun Fei, and Changxi Zheng. 2015. Interactive acoustic transfer approximation for modal sound. ACM Transactions on Graphics (Proceedings of SIGGRAPH 2015) 35, 1 (2015), 1–16.Google ScholarDigital Library
28. Shiguang Liu and Dinesh Manocha. 2020. Sound Synthesis, Propagation, and Rendering: A Survey. arXiv preprint arXiv:2011.05538 (2020).Google Scholar
29. Yijun Liu. 2009. Fast multipole boundary element method: theory and applications in engineering. Cambridge university press.Google Scholar
30. Ravish Mehra, Nikunj Raghuvanshi, Lakulish Antani, Anish Chandak, Sean Curtis, and Dinesh Manocha. 2013. Wave-based sound propagation in large open scenes using an equivalent source formulation. ACM Transactions on Graphics (Proceedings of SIGGRAPH 2013) 32, 2 (2013), 1–13.Google ScholarDigital Library
31. Hsien-Yu Meng, Zhenyu Tang, and Dinesh Manocha. 2021. Point-based Acoustic Scattering for Interactive Sound Propagation via Surface Encoding. CoRR abs/2105.08177 (2021).Google Scholar
32. James F. O’Brien, Chen Shen, and Christine M. Gatchalian. 2002. Synthesizing Sounds from Rigid-Body Simulations. In Proceedings of the 2002 ACM SIGGRAPH/Eurographics Symposium on Computer Animation (San Antonio, Texas) (SCA ’02). Association for Computing Machinery, New York, NY, USA, 175–181.Google Scholar
33. Dinesh K Pai, Kees van den Doel, Doug L James, Jochen Lang, John E Lloyd, Joshua L Richmond, and Som H Yau. 2001. Scanning physical interaction behavior of 3D objects. In Proceedings of the 28th annual conference on Computer graphics and interactive techniques. 87–96.Google Scholar
34. Charles Ruizhongtai Qi, Li Yi, Hao Su, and Leonidas J Guibas. 2017. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. In Advances in neural information processing systems. 5099–5108.Google Scholar
35. Nikunj Raghuvanshi and Ming C Lin. 2006. Interactive sound synthesis for large scale environments. In Proceedings of the 2006 symposium on Interactive 3D graphics and games. 101–108.Google ScholarDigital Library
36. Anton Ratnarajah, Shi-Xiong Zhang, Meng Yu, Zhenyu Tang, Dinesh Manocha, and Dong Yu. 2021. FAST-RIR: Fast neural diffuse room impulse response generator. Google ScholarCross Ref
37. Zhimin Ren, Hengchin Yeh, and Ming C Lin. 2013. Example-guided physically based modal sound synthesis. ACM Transactions on Graphics (Proceedings of SIGGRAPH 2013) 32, 1 (2013), 1–16.Google ScholarDigital Library
38. Olaf Ronneberger, Philipp Fischer, and Thomas Brox. 2015. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical image computing and computer-assisted intervention. Springer, 234–241.Google ScholarCross Ref
39. Atul Rungta, Carl Schissler, Ravish Mehra, Chris Malloy, Ming Lin, and Dinesh Manocha. 2016. SynCoPation: Interactive synthesis-coupled sound propagation. IEEE transactions on visualization and computer graphics 22, 4 (2016), 1346–1355.Google Scholar
40. Ahmed A Shabana. 1991. Theory of vibration. Vol. 2. Springer.Google Scholar
41. Auston Sterling, Nicholas Rewkowski, Roberta L Klatzky, and Ming C Lin. 2019. Audio-material reconstruction for virtualized reality using a probabilistic damping model. IEEE transactions on visualization and computer graphics 25, 5 (2019), 1855–1864.Google ScholarCross Ref
42. Hang Su, Subhransu Maji, Evangelos Kalogerakis, and Erik Learned-Miller. 2015. Multi-view convolutional neural networks for 3d shape recognition. In Proceedings of the IEEE international conference on computer vision. 945–953.Google ScholarDigital Library
43. Zhenyu Tang, Rohith Aralikatti, Anton Ratnarajah, and Dinesh Manocha. 2022. GWA: A Large High-Quality Acoustic Dataset for Audio Processing. Google ScholarCross Ref
44. Kees van de Doel and Dinesh K Pai. 1996. Synthesis of shape dependent sounds with physical modeling. Georgia Institute of Technology.Google Scholar
45. Kees van den Doel, Paul G. Kry, and Dinesh K. Pai. 2001. FoleyAutomatic: Physically-Based Sound Effects for Interactive Simulation and Animation (SIGGRAPH ’01). Association for Computing Machinery, New York, NY, USA.Google Scholar
46. Jui-Hsien Wang and Doug L. James. 2019. KleinPAT: Optimal Mode Conflation for Time-domain Precomputation of Acoustic Transfer. ACM Transactions on Graphics (Proceedings of SIGGRAPH 2019) 38, 4, Article 122 (July 2019), 12 pages.Google Scholar
47. Zhirong Wu, Shuran Song, Aditya Khosla, Fisher Yu, Linguang Zhang, Xiaoou Tang, and Jianxiong Xiao. 2015. 3D shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE conference on computer vision and pattern recognition. 1912–1920.Google Scholar
48. Tianxiang Zhang, Sheng Li, Dinesh Manocha, Guoping Wang, and Hanqiu Sun. 2015. Quadratic Contact Energy Model for Multi-impact Simulation. In Computer Graphics Forum, Vol. 34. Wiley Online Library, 133–144.Google Scholar
49. Changxi Zheng and Doug L James. 2010. Rigid-body fracture sound with precomputed soundbanks. In ACM SIGGRAPH 2010 papers. 1–13.Google ScholarDigital Library
50. Changxi Zheng and Doug L James. 2011. Toward high-quality modal contact sound. In ACM SIGGRAPH 2011 papers. 1–12.Google ScholarDigital Library