“Multi-Resolution Approach to Computing Locally Injective Maps on Meshes” by Naitsat and Zeevi
Conference:
Type(s):
Entry Number: 87
Title:
- Multi-Resolution Approach to Computing Locally Injective Maps on Meshes
Presenter(s)/Author(s):
Abstract:
INTRODUCTION
Computing injective mappings with low distortions on meshes is an important problem for its wide range of practical applications in computer graphics, geometric modeling and physical simulations. Such tasks as surface parameterization or shape deformation are often reduced to minimizing non-convex and non-linear geometric energies defined over triangulated domains. These energies are commonly expressed in a finite element manner as a weighted sum of distortion densities D over simplexes S: E (f [x]) = Õ s ∈S w(s)D(Js ), where x is the column stack of vertex positions under piecewise affine mapping f and Js denotes the Jacobian of f on s, modulo a rigid transformation of s to its target shape. Usually, a proper minimizer of (1) has to satisfy the following constraints: det(Js ) > 0, ∀s ∈ S; (2) Ax = b , (3) where (2) enforces f to preserve orientation of each simplex, and (A,b) is a linear system of the given positional constraints. The orientation constraints are particularly important in parameterization problems, since they avoid undesirable foldover artifacts in the texture, while positional constraints are widely used in shape deformation applications, such as point-to-point deformations, deformations with fixed anchors, and more.
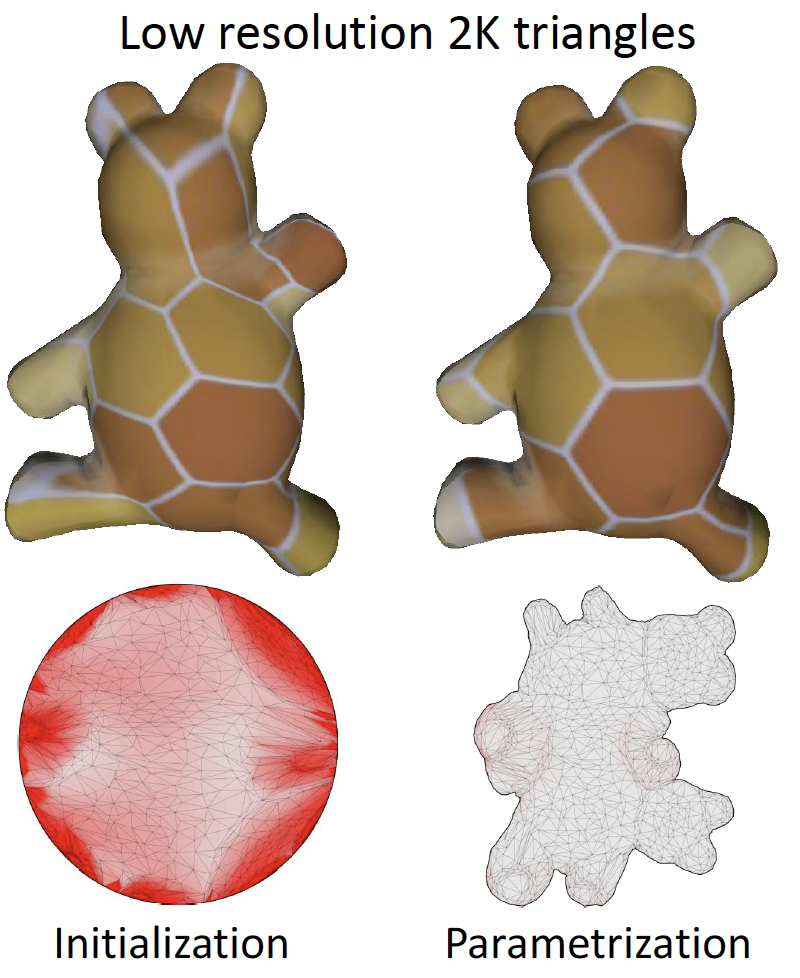
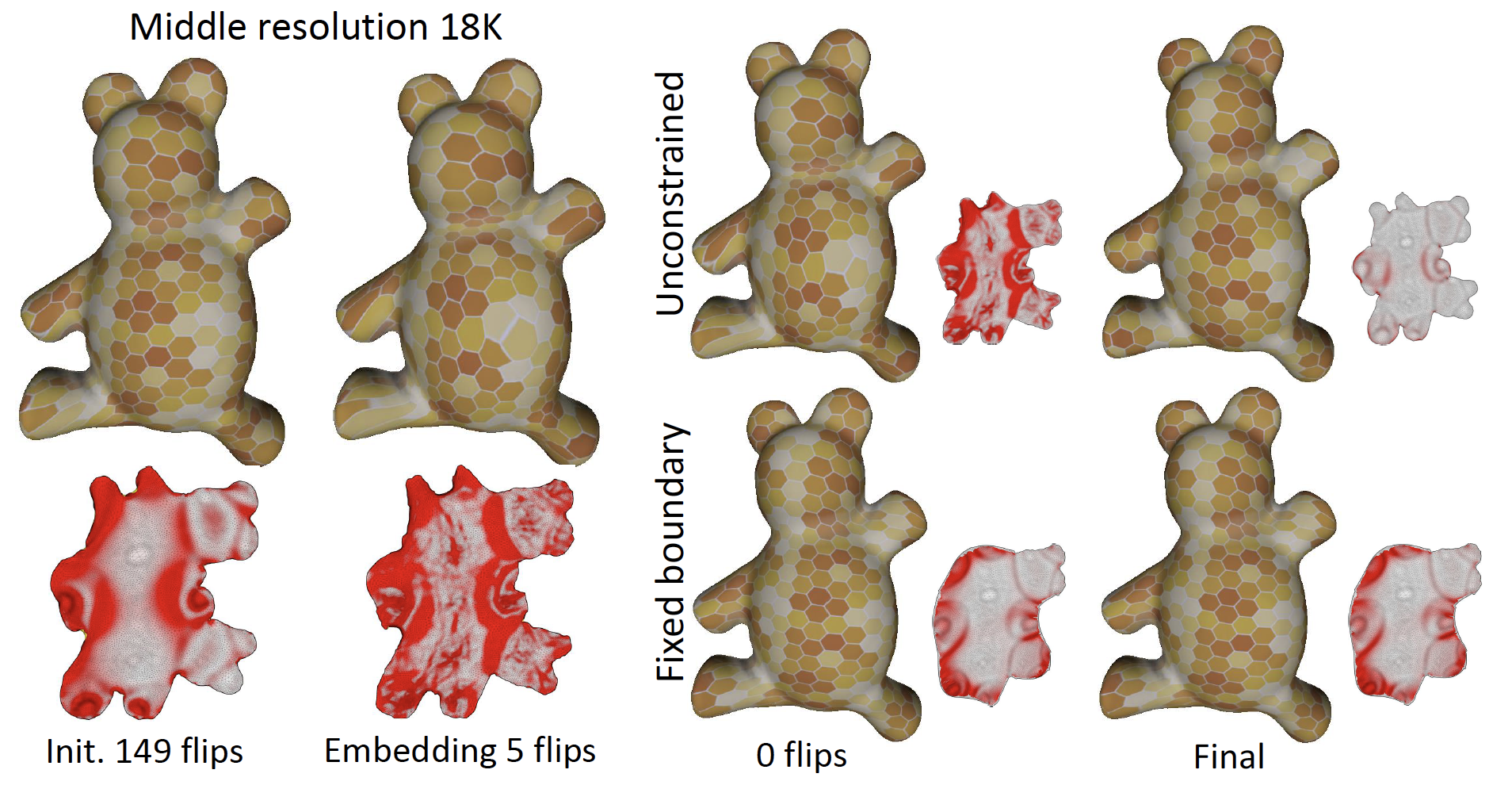
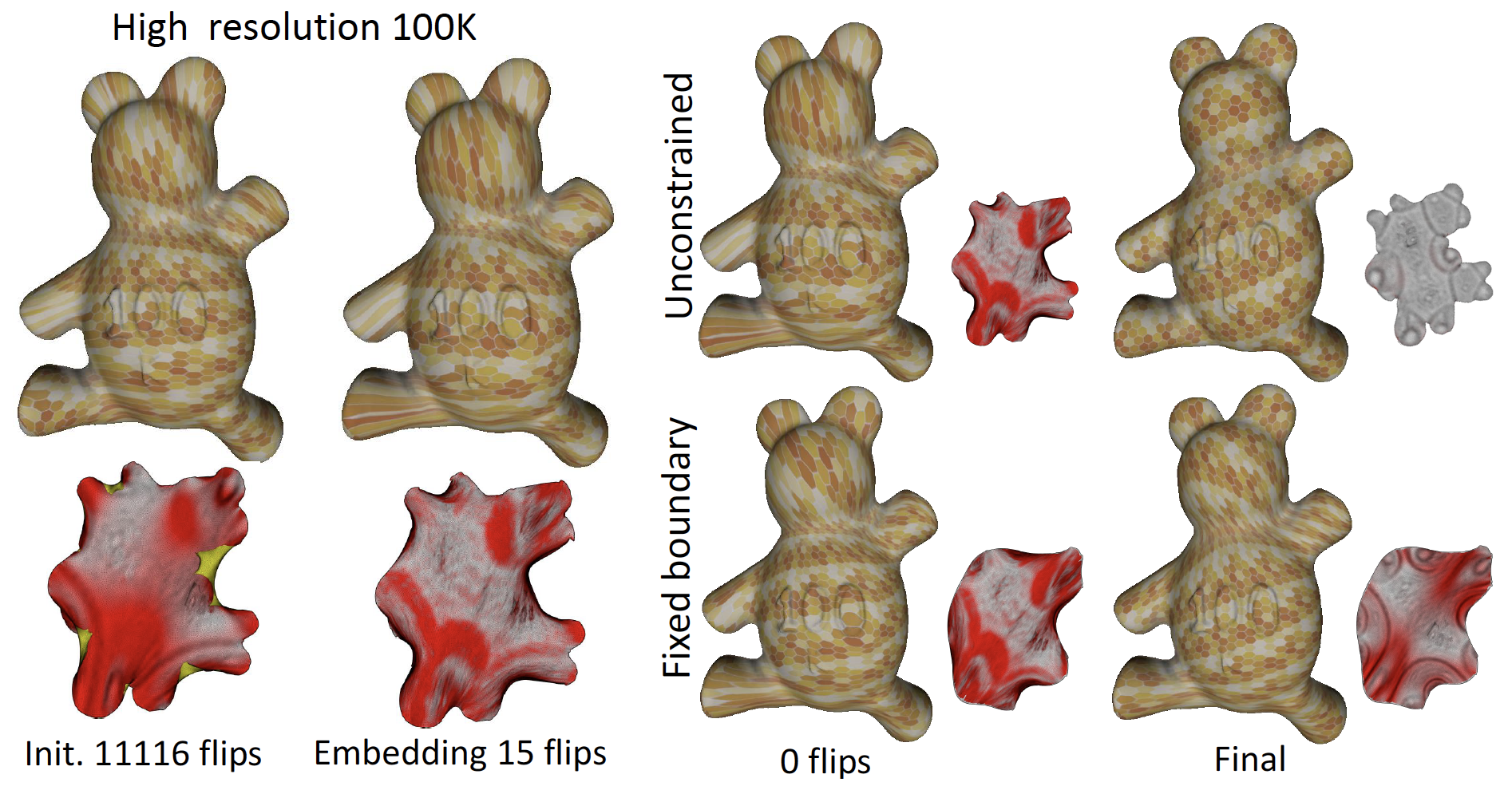
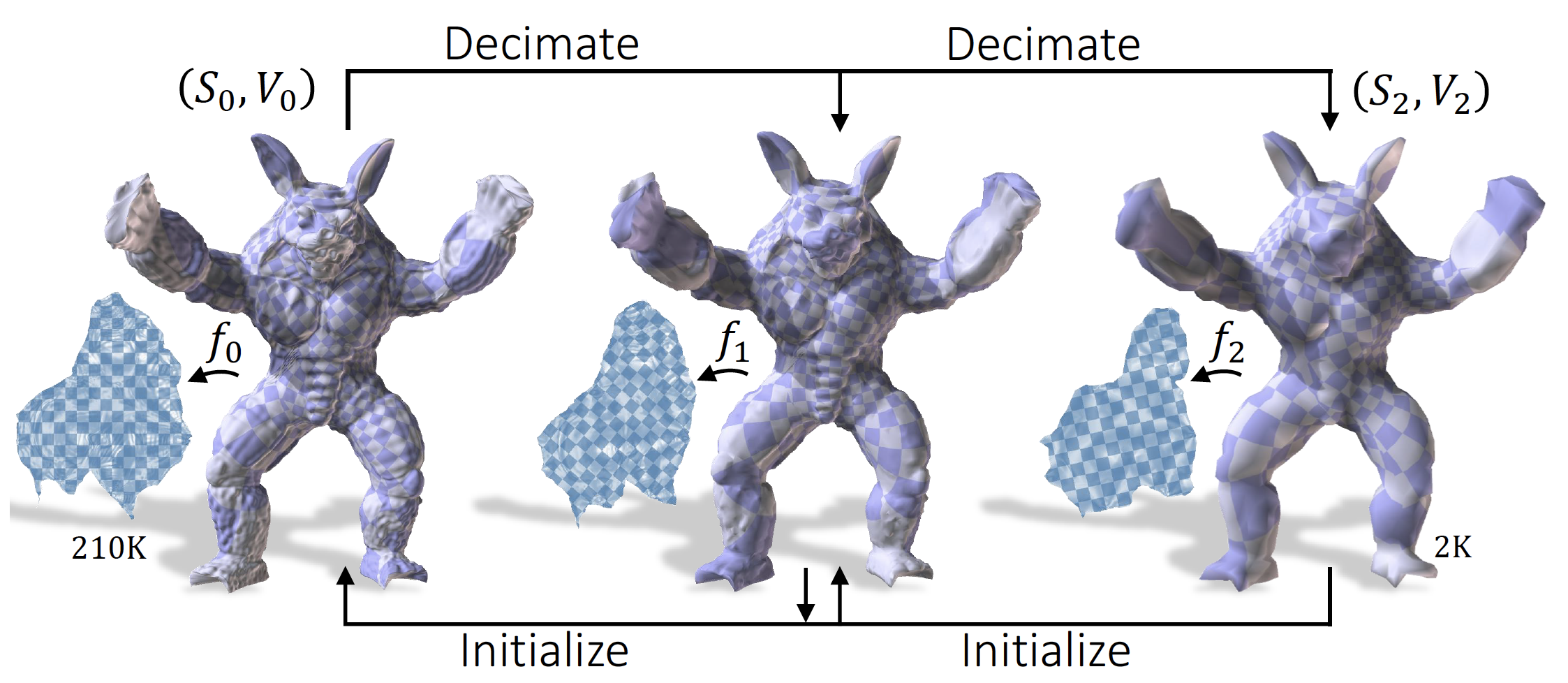
In this work we propose a multi-resolution approach to construction of injective maps with low distortions in 2D and 3D, by initializing the optimization of (1) with the solution of the same problem in a lower resolution. In certain aspects our approach extends the recently proposed Progressive Parametrization [Liu et al. 2018], by decomposing the objective map f into a number of intermediate mappings with decreasing distortions and diminishing number of simplexes.
Although our approach is simple and intuitive, it has not been yet properly implemented on meshes due to the following major limitations of state-of-the-art methods: i) fast optimizers of (1) have to be initialized by an injective map f 0 [Claici et al. 2017; Rabinovich et al. 2017; Shtengel et al. 2017; Zhu et al. 2018]; ii) solvers that can handle non-injective initializations are either slow and hardly scalable [Kovalsky et al. 2014], or require a user assistance (non-automatic) [Poranne et al. 2017]; iii) methods for computing injective maps are effective only in simple configurations [Aigerman and Lipman 2013; Fu and Liu 2016; Kovalsky et al. 2015].
Despite the long history of multi-resolution algorithms in computer graphics, dating back to the late 90s [Lee et al. 1998], the vast majority of these methods operate over multigrid domains, spline-based models and subdivision surfaces. Due to the aforementioned difficulties in processing non-locally injective maps, multi-resolution methods have surprisingly failed, so far, to perform competitively on meshes. In our method, the non-injective initialization obstacle, often occurring during transitions between multiple resolutions, is overcome by simultaneously repairing inverted elements and minimizing distortions by means of a novel Multi-Objective Block Coordinate Descent (MBCD) algorithm [Naitsat and Zeevi 2019]. MBCD is an adaptive local-global solver that alternates between distortion energies (1) and inverted element penalties which are optimized in coordinate blocks of varying sizes.
References:
- Noam Aigerman and Yaron Lipman. 2013. Injective and bounded distortion mappings in 3D. ACM Trans. Graph 32, 4 (2013), 106:1–106:14.
- S Claici, M Bessmeltsev, S Schaefer, and J Solomon. 2017. Isometry-Aware Preconditioning for Mesh Parameterization. In Computer Graphics Forum, Vol. 36. Wiley Online Library, 37–47.
- Michael Floater. 2003. One-to-one piecewise linear mappings over triangulations. Math. Comp. 72, 242 (2003), 685–696.
- Xiao-Ming Fu and Yang Liu. 2016. Computing inversion-free mappings by simplex assembly. ACM Transactions on Graphics (TOG) 35, 6 (2016), 216.
- Shahar Z Kovalsky, Noam Aigerman, Ronen Basri, and Yaron Lipman. 2014. Controlling Singular Values with Semidefinite Programming. ACM Transactions on Graphics (TOG) 33, 4 (2014), 68.
- Shahar Z Kovalsky, Noam Aigerman, Ronen Basri, and Yaron Lipman. 2015. Large-scale bounded distortion mappings. ACM Trans. Graph 34, 6 (2015), 191.
- Aaron WF Lee, Wim Sweldens, Peter Schröder, Lawrence C Cowsar, and David P Dobkin. 1998. MAPS: Multiresolution adaptive parameterization of surfaces. In Siggraph, Vol. 98. 95–104.
- Ligang Liu, Chunyang Ye, Ruiqi Ni, and Xiao-Ming Fu. 2018. Progressive parameterizations. ACM Transactions on Graphics (TOG) 37, 4 (2018), 41.
- Alexander Naitsat and Y. Yehoshua Zeevi. 2019. Adaptive block coordinate descent for distortion minimization. In Proceedings of the Symposium on Geometry Processing, to appear. Eurographics Association.
- Roi Poranne, Marco Tarini, Sandro Huber, Daniele Panozzo, and Olga Sorkine-Hornung. 2017. Autocuts: simultaneous distortion and cut optimization for UV mapping. ACM Transactions on Graphics (TOG) 36, 6 (2017), 215.
- Michael Rabinovich, Roi Poranne, Daniele Panozzo, and Olga Sorkine-Hornung. 2017. Scalable locally injective mappings. ACM Transactions on Graphics (TOG) 36, 2 (2017), 16.
- Anna Shtengel, Roi Poranne, Olga Sorkine-Hornung, Shahar Z Kovalsky, and Yaron Lipman. 2017. Geometric optimization via composite majorization. ACM Trans. Graph 36, 4 (2017), 38.
- Yin Xu, Renjie Chen, Craig Gotsman, and Ligang Liu. 2011. Embedding a triangular graph within a given boundary. Computer Aided Geometric Design 28, 6 (2011), 349–356.
- Yufeng Zhu, Robert Bridson, and Danny M Kaufman. 2018. Blended cured quasi newton for distortion optimization. ACM Transactions on Graphics (TOG) 37, 4 (2018), 40.
Keyword(s):
Acknowledgements:
Research has been supported in part by the Ollendorff Minerva Center.