“Meta-representation of shape families” by Fish, Averkiou, Kaick, Sorkine-Hornung, Cohen-Or, et al. …
Conference:
Type(s):
Title:
- Meta-representation of shape families
Session/Category Title: Shape Collection
Presenter(s)/Author(s):
Moderator(s):
Abstract:
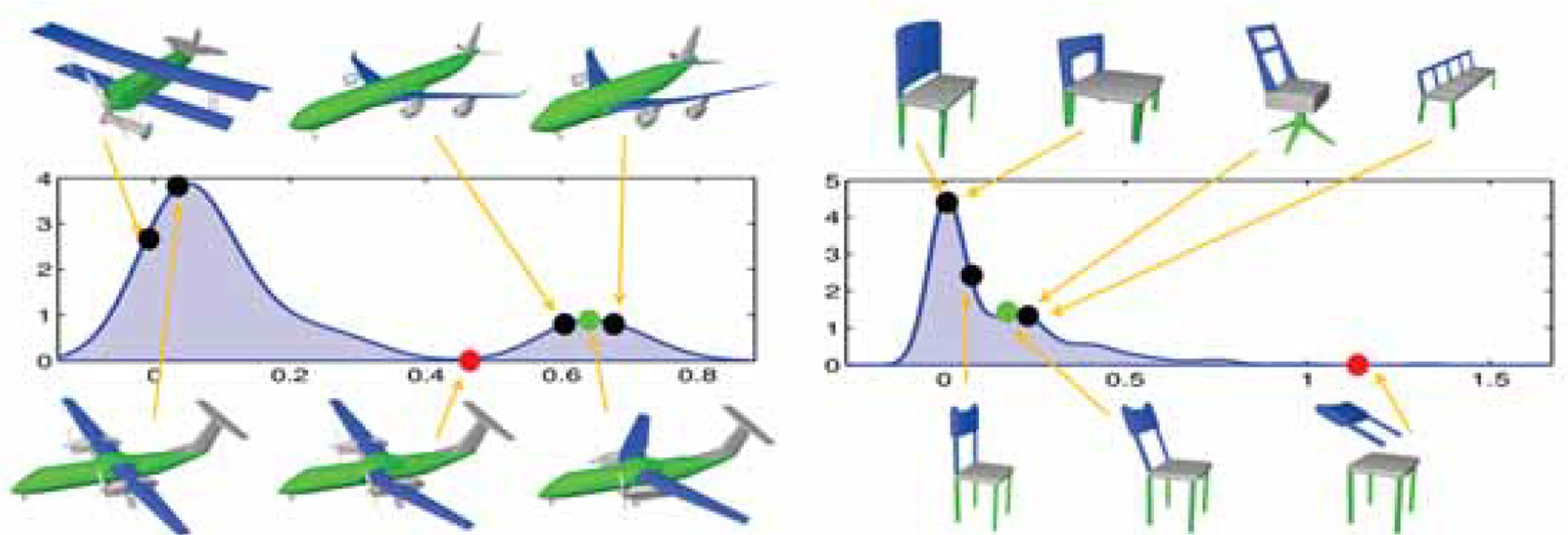
We introduce a meta-representation that represents the essence of a family of shapes. The meta-representation learns the configurations of shape parts that are common across the family, and encapsulates this knowledge with a system of geometric distributions that encode relative arrangements of parts. Thus, instead of predefined priors, what characterizes a shape family is directly learned from the set of input shapes. The meta-representation is constructed from a set of co-segmented shapes with known correspondence. It can then be used in several applications where we seek to preserve the identity of the shapes as members of the family. We demonstrate applications of the meta-representation in exploration of shape repositories, where interesting shape configurations can be examined in the set; guided editing, where models can be edited while maintaining their familial traits; and coupled editing, where several shapes can be collectively deformed by directly manipulating the distributions in the meta-representation. We evaluate the efficacy of the proposed representation on a variety of shape collections.
References:
1. Averkiou, M., Kim, V. G., Zheng, Y., and Mitra, N. J. 2014. Shapesynth: Parameterizing model collections for coupled shape exploration and synthesis. Computer Graphics Forum (Eurographics) 33.Google Scholar
2. Bokeloh, M., Wand, M., and Seidel, H.-P. 2010. A connection between partial symmetry and inverse procedural modeling. ACM Trans. Graph (SIGGRAPH) 29, 4, 104: 1–10. Google ScholarDigital Library
3. Botsch, M., and Sorkine, O. 2008. On linear variational surface deformation methods. IEEE Trans. Vis. & Comp. Graphics 14, 1, 213–230. Google ScholarDigital Library
4. Chaudhuri, S., Kalogerakis, E., Guibas, L., and Koltun, V. 2011. Probabilistic reasoning for assembly-based 3D modeling. ACM Trans. Graph (SIGGRAPH) 30, 4, 35: 1–10. Google ScholarDigital Library
5. Chiu, S.-T. 1996. A comparative review of bandwidth selection for kernel density estimation. Statistica Sinica 6, 1, 129–145.Google Scholar
6. Fisher, M., Savva, M., and Hanrahan, P. 2011. Characterizing structural relationships in scenes using graph kernels. ACM Trans. Graph (SIGGRAPH) 30, 4, 34: 1–12. Google ScholarDigital Library
7. Funkhouser, T., Kazhdan, M., Shilane, P., Min, P., Kiefer, W., Tal, A., Rusinkiewicz, S., and Dobkin, D. 2004. Modeling by example. ACM Trans. Graph (SIGGRAPH) 23, 3, 652–663. Google ScholarDigital Library
8. Gal, R., Sorkine, O., Mitra, N. J., and Cohen-Or, D. 2009. iWIRES: An analyze-and-edit approach to shape manipulation. ACM Trans. Graph (SIGGRAPH) 28, 3, 33: 1–10. Google ScholarDigital Library
9. Hu, R., Fan, L., and Liu, L. 2012. Co-segmentation of 3D shapes via subspace clustering. Computer Graphics Forum (SGP) 31, 5, 1703–1713. Google ScholarDigital Library
10. Huang, Q., Koltun, V., and Guibas, L. 2011. Joint shape segmentation with linear programming. ACM Trans. Graph (SIGGRAPH Asia) 30, 6, 125: 1–12. Google ScholarDigital Library
11. Kalogerakis, E., Hertzmann, A., and Singh, K. 2010. Learning 3D mesh segmentation and labeling. ACM Trans. Graph (SIGGRAPH) 29, 3, 102: 1–12. Google ScholarDigital Library
12. Kalogerakis, E., Chaudhuri, S., Koller, D., and Koltun, V. 2012. A probabilistic model of component-based shape synthesis. ACM Trans. Graph (SIGGRAPH) 31, 4, 55: 1–11. Google ScholarDigital Library
13. Kim, V. G., Li, W., Mitra, N. J., Chaudhuri, S., DiVerdi, S., and Funkhouser, T. 2013. Learning part-based templates from large collections of 3D shapes. ACM Trans. Graph (SIGGRAPH) 32, 4, 70: 1–12. Google ScholarDigital Library
14. Laga, H., Mortara, M., and Spagnuolo, M. 2013. Geometry and context for semantic correspondences and functionality recognition in man-made 3D shapes. ACM Trans. Graph 32, 5, 150: 1–16. Google ScholarDigital Library
15. Li, G., Liu, L., Zheng, H., and Mitra, N. J. 2010. Analysis, reconstruction and manipulation using arterial snakes. ACM Trans. Graph (SIGGRAPH Asia) 29, 6, 152: 1–10. Google ScholarDigital Library
16. Lin, J., Cohen-Or, D., Zhang, H. R., Liang, C., Sharf, A., Deussen, O., and Chen, B. 2011. Structure-preserving re-targeting of irregular 3D architecture. ACM Trans. Graph (SIGGRAPH Asia) 30, 6, 183: 1–10. Google ScholarDigital Library
17. Meng, M., Xia, J., Luo, J., and He, Y. 2013. Unsupervised co-segmentation for 3D shapes using iterative multi-label optimization. Computer-Aided Design 45, 2, 312–320. Google ScholarDigital Library
18. Mitra, N. J., Wand, M., Zhang, H., Cohen-Or, D., and Bokeloh, M. 2013. Structure-aware shape processing. In Proc. Eurographics State-of-the-art Reports.Google Scholar
19. Ovsjanikov, M., Li, W., Guibas, L., and Mitra, N. J. 2011. Exploration of continuous variability in collections of 3D shapes. ACM Trans. Graph (SIGGRAPH) 30, 4, 33: 1–10. Google ScholarDigital Library
20. Schneider, P. J., and Eberly, D. H. 2003. Geometric Tools for Computer Graphics. Morgan Kaufmann, San Francisco. Google ScholarDigital Library
21. Shtof, A., Agathos, A., Gingold, Y., Shamir, A., and Cohen-Or, D. 2013. Geosemantic snapping for sketch-based modeling. Computer Graphics Forum (Eurographics) 32, 2, 245–253.Google ScholarCross Ref
22. Sidi, O., van Kaick, O., Kleiman, Y., Zhang, H., and Cohen-Or, D. 2011. Unsupervised co-segmentation of a set of shapes via descriptor-space spectral clustering. ACM Trans. Graph (SIGGRAPH Asia) 30, 6, 126: 1–10. Google ScholarDigital Library
23. Silverman, B. W. 1986. Density Estimation for Statistics and Data Analysis. Chapman & Hall, London.Google Scholar
24. Sorkine, O., and Alexa, M. 2007. As-rigid-as-possible surface modeling. In Symp. Geometry Processing, 109–116. Google ScholarDigital Library
25. Sumner, R. W., Zwicker, M., Gotsman, C., and Popović, J. 2005. Mesh-based inverse kinematics. ACM Trans. Graph (SIGGRAPH) 24, 3, 488–495. Google ScholarDigital Library
26. van Kaick, O., Xu, K., Zhang, H., Wang, Y., Sun, S., Shamir, A., and Cohen-Or, D. 2013. Co-hierarchical analysis of shape structures. ACM Trans. Graph (SIGGRAPH) 32, 4, 69: 1–10. Google ScholarDigital Library
27. Wang, Y., Asafi, S., van Kaick, O., Zhang, H., Cohen-Or, D., and Chen, B. 2012. Active co-analysis of a set of shapes. ACM Trans. Graph (SIGGRAPH Asia) 31, 6, 157: 1–10. Google ScholarDigital Library
28. Xu, W., Wang, J., Yin, K., Zhou, K., van de Panne, M., Chen, F., and Guo, B. 2009. Joint-aware manipulation of deformable models. ACM Trans. Graph (SIGGRAPH) 28, 3, 35: 1–9. Google ScholarDigital Library
29. Xu, K., Zhang, H., Cohen-Or, D., and Chen, B. 2012. Fit and diverse: Set evolution for inspiring 3D shape galleries. ACM Trans. Graph (SIGGRAPH) 31, 4, 57: 1–10. Google ScholarDigital Library
30. Yang, Y.-L., Yang, Y.-J., Pottmann, H., and Mitra, N. J. 2011. Shape space exploration of constrained meshes. ACM Trans. Graph (SIGGRAPH Asia) 30, 6, 124:1–124:12. Google ScholarDigital Library
31. Yumer, M. E., and Kara, L. B. 2012. Co-abstraction of shape collections. ACM Trans. Graph (SIGGRAPH Asia) 31, 6, 166: 1–11. Google ScholarDigital Library
32. Zheng, Y., Fu, H., Cohen-Or, D., Au, O. K.-C., and Tai, C.-L. 2011. Component-wise controllers for structure-preserving shape manipulation. Computer Graphics Forum (Eurographics) 30, 2, 563–572.Google ScholarCross Ref
33. Zheng, Y., Cohen-Or, D., and Mitra, N. J. 2013. Smart variations: Functional substructures for part compatibility. Computer Graphics Forum (Eurographics) 32, 2, 195–204.Google ScholarCross Ref
34. Zheng, Y., Cohen-Or, D., Averkiou, M., and Mitra, N. J. 2014. Recurring part arrangements in shape collections. Computer Graphics Forum (Eurographics) 33.Google Scholar