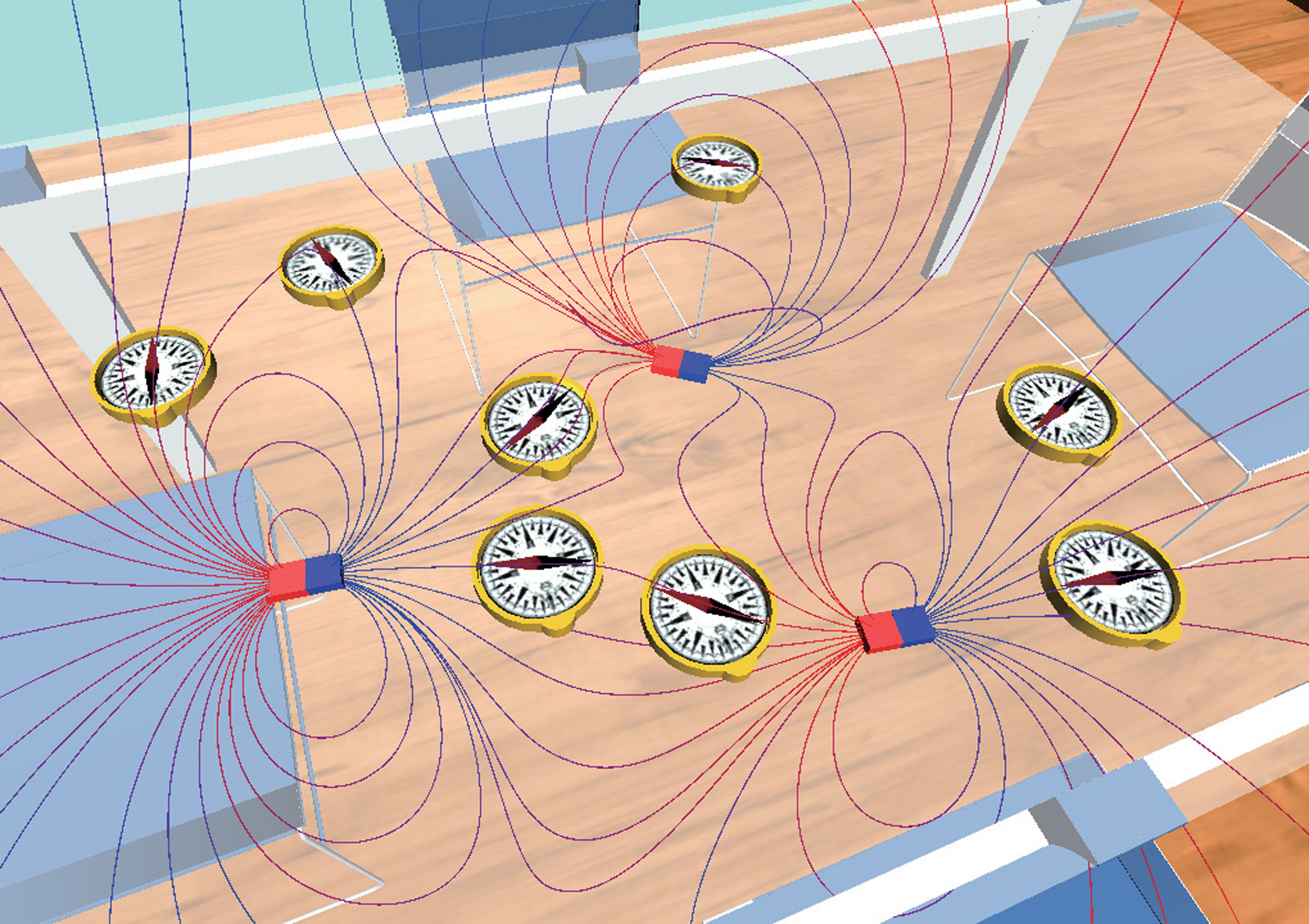
“Magnetization dynamics for magnetic object interactions” by Kim, Park and Han
Conference:
Type(s):
Entry Number: 121
Title:
- Magnetization dynamics for magnetic object interactions
Session/Category Title: Deep Thoughts on How Things Move
Presenter(s)/Author(s):
Moderator(s):
Abstract:
The goal of this paper is to simulate the interactions between magnetic objects in a physically correct way. The simulation scheme is based on magnetization dynamics, which describes the temporal change of magnetic moments. For magnetization dynamics, the Landau-Lifshitz-Gilbert equation is adopted, which is widely used in micromagnetics. Through effectively-designed novel models of magnets, it is extended into the macro scale so as to be combined with real-time rigid-body dynamics. The overall simulation is stable and enables us to implement mutual induction and remanence that have not been tackled by the state-of-the-art technique in magnet simulation. The proposed method can be applied to various fields including magnet experiments in the virtual world.
References:
1. JJ Abbott, O Ergeneman, MP Kummer, AM Hirt, and BJ Nelson. 2007. Modeling magnetic torque and force for controlled manipulation of soft-magnetic bodies. IEEE Transactions on Robotics 23, 6 (2007), 1247–1252. Google ScholarDigital Library
2. A Aharoni. 2000. Introduction to the Theory of Ferromagnetism. Vol. 109. Clarendon Press.Google Scholar
3. S Bachthaler, F Sadlo, R Weeber, S Kantorovich, C Holm, and D Weiskopf. 2012. Magnetic flux topology of 2D point dipoles. In Computer Graphics Forum, Vol. 31. Wiley Online Library, 955–964. Google ScholarDigital Library
4. M Beleggia and M De Graef. 2005. General magnetostatic shape-shape interactions. Journal of Magnetism and Magnetic Materials 285, 1–2 (2005), L1–L10.Google ScholarCross Ref
5. W Brown. 1979. Thermal fluctuation of fine ferromagnetic particles. IEEE Transactions on Magnetics 15, 5 (1979), 1196–1208.Google ScholarCross Ref
6. Q Cao, X Han, and L Li. 2014. Configurations and control of magnetic fields for manipulating magnetic particles in microfluidic applications: magnet systems and manipulation mechanisms. Lab on a Chip 14, 15 (2014), 2762–2777.Google Scholar
7. E Coumans. 2015. Bullet physics simulation. In ACM SIGGRAPH 2015 Courses. ACM, 7. Google ScholarDigital Library
8. M d’Aquino. 2005. Nonlinear magnetization dynamics in thin-films and nanoparticles. Ph.D. Dissertation. Università degli Studi di Napoli Federico II.Google Scholar
9. M De Graef and M Beleggia. 2009. General magnetostatic shape-shape interaction forces and torques. Journal of Magnetism and Magnetic Materials 321, 15 (2009), L45–L51.Google ScholarCross Ref
10. M d’Aquino, C Serpico, and G Miano. 2005. Geometrical integration of Landau-Lifshitz-Gilbert equation based on the mid-point rule. J. Comput. Phys. 209, 2 (2005), 730–753. Google ScholarDigital Library
11. TL Gilbert. 1955. A Lagrangian formulation of the gyromagnetic equation of the magnetization field. Phys. Rev. 100 (1955), 1243.Google Scholar
12. R Grössinger. 1981. A critical examination of the law of approach to saturation. I. Fit procedure, physica status solidi (a) 66, 2 (1981), 665–674.Google Scholar
13. GF Herrmann. 1963. Resonance and high frequency susceptibility in canted antiferromagnetic substances. Journal of Physics and Chemistry of Solids 24, 5 (1963), 597–606.Google ScholarCross Ref
14. T Ishikawa, Y Yue, K Iwasaki, Y Dobashi, and T Nishita. 2013. Visual Simulation of Magnetic Fluid Using a Procedural Approach for Spikes Shape. In Computer Vision, Imaging and Computer Graphics. Theory and Application. Springer, 112–126.Google Scholar
15. JD Jackson. 1999. Classical electrodynamics. American Journal of Physics 67, 9 (1999), 841–842.Google ScholarCross Ref
16. W Jakob. 2010. Mitsuba renderer. (2010). http://www.mitsuba-renderer.org.Google Scholar
17. R Khymyn, I Lisenkov, V Tiberkevich, BA Ivanov, and A Slavin. 2017. Antiferromagnetic THz-frequency Josephson-like Oscillator Driven by Spin Current. Scientific Reports 7 (2017), 43705.Google ScholarCross Ref
18. T Klein and T Ertl. 2004. Illustrating Magnetic Field Lines using a Discrete Particle Model.. In VMV, Vol. 4. 387–394.Google Scholar
19. M Kruzík and A Prohl. 2006. Recent developments in the modeling, analysis, and numerics of ferromagnetism. SIAM review 48, 3 (2006), 439–483. Google ScholarDigital Library
20. M Lakshmanan. 2011. The fascinating world of the Landau-Lifshitz-Gilbert equation: an overview. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 369, 1939 (2011), 1280–1300.Google Scholar
21. R Moskowitz and E Della Torre. 1966. Theoretical aspects of demagnetization tensors. IEEE Transactions on Magnetics 2, 4 (1966), 739–744.Google ScholarCross Ref
22. M Müller, D Charypar, and M Gross. 2003. Particle-based fluid simulation for interactive applications. In Proceedings of the 2003 ACM SIGGRAPH/Eurographics symposium on Computer animation. Eurographics Association, 154–159. Google ScholarDigital Library
23. Y Nakatani, Y Uesaka, and N Hayashi. 1989. Direct solution of the Landau-Lifshitz-Gilbert equation for micromagnetics. Japanese Journal of Applied Physics 28, 12R (1989), 2485.Google ScholarCross Ref
24. JA Osborn. 1945. Demagnetizing factors of the general ellipsoid. Physical review 67, 11–12 (1945), 351.Google Scholar
25. J Park, K Lee, and J Han. 2016. Interactive visualization of magnetic field for virtual science experiments. Journal of Visualization 19, 1 (2016), 129–139. Google ScholarDigital Library
26. P Podio-Guidugli. 2001. On dissipation mechanisms in micromagnetics. The European Physical Journal B-Condensed Matter and Complex Systems 19, 3 (2001), 417–424.Google ScholarCross Ref
27. C Serpico, ID Mayergoyz, and G Bertotti. 2001. Numerical technique for integration of the Landau-Lifshitz equation. Journal of Applied Physics 89, 11 (2001), 6991–6993.Google ScholarCross Ref
28. B Thomaszewski, A Gumann, S Pabst, and W Strasser. 2008. Magnets in Motion. In ACM SIGGRAPH Asia 2008 Papers (SIGGRAPH Asia ’08). ACM, New York, NY, USA, Article 162, 9 pages. Google ScholarDigital Library
29. W Yoon, N Lee, K Urn, and J Han. 2014. Computer-gene rated iron filing art. The Visual Computer 30, 6–8 (2014), 889–895. Google ScholarDigital Library