“Low cost illumination computation using an approximation of light wavefronts” by Elber
Conference:
Type(s):
Title:
- Low cost illumination computation using an approximation of light wavefronts
Presenter(s)/Author(s):
Abstract:
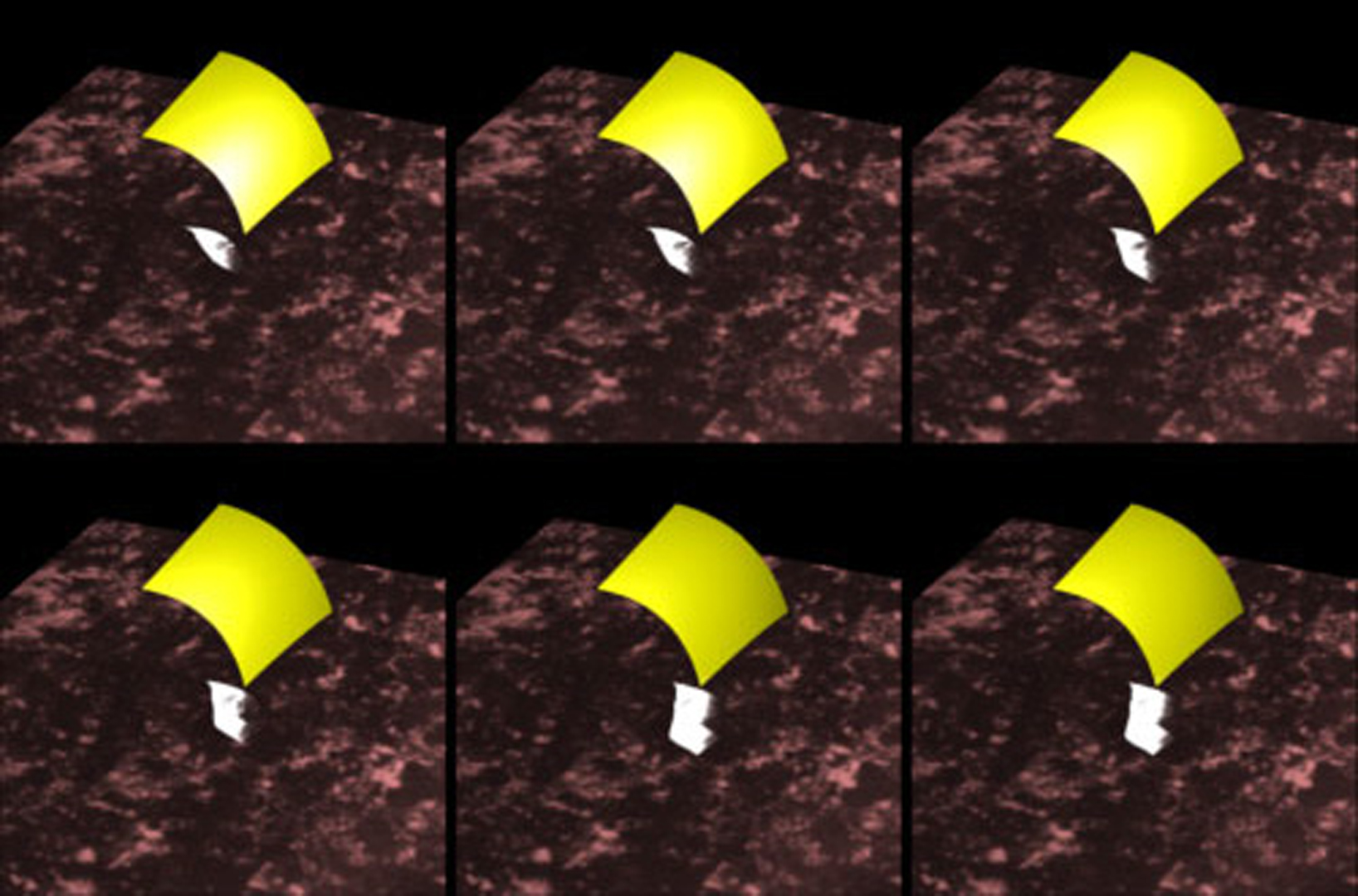
We present an efficient method to simulate the propagation of wavefronts and approximate the behavior of light in an environment of freeform surfaces. The proposed method can emulate the behavior of a wavefront emanating from a point or spherical light source, and possibly refracted and/or reflected from a freeform surface. Moreover, it allows one to consider and to render images with extreme illumination conditions such as caustics.The proposed method can be embedded into rendering schemes that are based on scan conversion. Using a direct freedom surface Z buffer renderer, we also demonstrate the use of the wavefront approximation in illumination computation.
References:
1. P. Atherton, K. Weiler, D. Greenberg. Polygon Shadow Gen-eration. Computer Graphics, Vol. 12, No. 3, pp 275-281, 1978.
2. P. Bergeron. A General Version of Crow’s Shadow Volumes. IEEE CG&A Vol 6, No. 9, pp. 17-28, 1986.
3. W. Boehm. Inserting New Knots into B-spline Curves. Com-puter Aided Design, vol. 12, No. 4, pp. 199-201, July 1980.
4. S. Chang, M. Shantz, and R. Rocchetti. Rendering Cubic Curves and Surfaces with Integer Adaptive Forward Differ-encing. Computer Graphics, Vol. 23, No. 3, pp. 157-166, July 1989.
5. N. Chin, S. Feiner. Fast Object-Precision Shadow Generation for Area Light Source. Computer Graphics Special Issue, Symposium on Interactive 3D Graphics, March 1992.
6. B. Cobb. Design of Sculptured Surfaces Using The B-spline Representation. Ph.D. Thesis, University of Utah, Computer Science Department, June 1984.
7. E. Cohen, T. Lyche, and R. Riesenfeld. Discrete B-splines and Subdivision Techniques in Computer Aided Geometric Design and Computer Graphics. Computer Graphics and Im-age Processing, 14, pp. 87-111, 1980.
8. M. F. Cohen, S. E. Chen, J. R. Wallace, D. P. Greenberg. A Progressive Refinment Approach to Fast Radiosity Image Generation. Computer Graphics, Vol. 22, No. 4, pp. 75-84, August 1988.
9. S. Coquillart. Computing Offset of Bspline Curves. Computer Aided Design, vol. 19, No. 6, pp. 305-309, July/August 1987.
10. M. P. DoCarmo. Differential Geometry of Curves and Sur-faces. Prentice-Hall 1976.
11. G. Elber and E. Cohen. Adaptive Iso-Curves Based Rendering for Free Form Surfaces. Technical Report UUCS-92-040, Department of Computer Science, Univeristy of Utah.
12. G. Elber and E. Cohen. Error Bounded Variable Distance Off-set Operator for Free Form Curves and Surfaces. International Journal of Computational Geometry & Applications, Vol. 1, Num. 1, March 1991, pp. 67-78
13. G. Farin. Curves and Surfaces for Computer Aided Geometric Design. Academic Press, Inc. Second Edition 1990.
14. R. T. Farouki and J. C. A. Chastang. Curves and Surfaces in Geometrical Optics. Mathematical Methods in Computer Aided geometric Design II. T. Lyche and L. L. Schumaler (Eds.), pp. 239-260, Academic Press, 1992.
15. J. D. Foley et al. Computer Graphics, Principles and Prac-tice, Second Edition. Addison-Wesley Systems Programming Series, Jul. 1990.
16. G. Heflin and G. Elber. ShadowVolume Generation from Free Form Surfaces. Communicating with Virtual Worlds, Nadia Magnenat Thalmann and Daniel Thalmann (Eds.), Computer Graphics Internation 1993 (CGI 93), Lausanne Switzerland, June 1993.
17. J. Hoschek. Spline Approximation of Offset Curves. Com-puter Aided Geometric Design 5, pp. 33-40, 1988.
18. J. Hoschek and D. Lasser. Fundamentals of Computer Aided Geometric Design. A. K. Peters, English edition, 1993.
19. D. Mitchell and P. Hanrahan. Illumination from Curved Re-flectors. Computer Graphics, Vol. 26, No. 2, pp. 283-291, July 1992.
20. T. Nishita, T. W. Sederberg and M. Kakimoto. Ray Tracing Trimmed Rational Surface Patches. Computer Graphics, Vol. 24, No. 4, pp. 337-345, August 1990.
21. K. L. Paik. Trivariate B-Splines. Ms.Sc. Thesis, University of Utah, Computer Science Department, December 1991.
22. B. Pham. Offset Approximation of Uniform B-splines. Com-puter Aided Design, vol. 20, No. 8, pp. 471-474, October 1988.
23. O. N. Stavroudis. The optics of Ray, Wavefronts, and Caustics. Academic, 1972.